All subjects
All subjects
 All subjects
All subjects
Energie potentielle d'un jeu de flèchettes
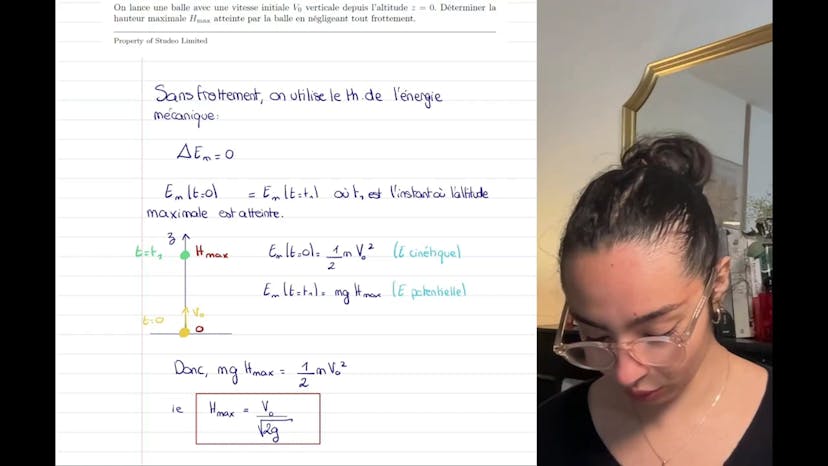
Aujourd'hui, nous allons faire un exercice sur l'énergie potentielle d'un jeu de fléchettes. Le problème est le suivant : un ressort de longueur à vide L0 égale à 10 cm est comprimé jusqu'à une longueur L1 de 4 cm. Lorsque le ressort est relâché, il permet de lancer des fléchettes d'une masse de 30 g qui atteignent une certaine altitude de 6 mètres lors d'un tir vertical. On nous donne également l'accélération de la pesanteur, qui est de 10 m/s². Notre objectif est de déterminer l'énergie mécanique totale d'une fléchette, ainsi que le niveau de référence pour l'énergie potentielle.
Pour commencer, nous pouvons faire un schéma de la situation. Le ressort est comprimé, et nous choisirons le niveau de référence pour l'énergie potentielle au niveau de l'extrémité du ressort lorsque celui-ci est comprimé. Lorsqu'il est tiré, le ressort se détend de 10 cm pour retrouver sa longueur à vide. L'énergie totale d'une fléchette est la somme de l'énergie potentielle et de l'énergie cinétique.
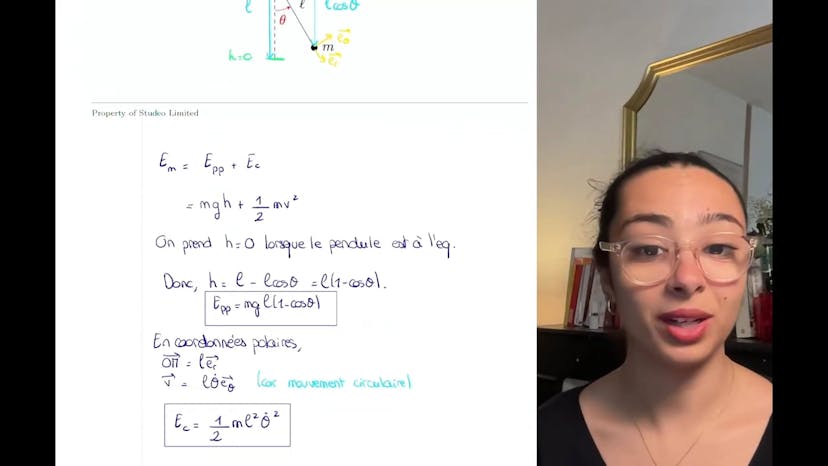
Pour calculer l'énergie potentielle élastique, qui est liée à la compression du ressort, nous utilisons la formule du cours : 1/2 * k * x², où x est la différence entre L et L0. Il y a également l'énergie potentielle de pesanteur, qui est égale à m * g * z, et l'énergie cinétique, qui est égale à 1/2 * m * v².
Pour déterminer le niveau de référence pour l'énergie potentielle, nous pouvons regarder les valeurs d'énergie potentielle de pesanteur et élastique lorsque z est égal à 0. Nous constatons que l'énergie potentielle de pesanteur est nulle, mais nous devons vérifier l'énergie potentielle élastique à ce niveau. [Note : l'orateur se trompe ici en disant que l'énergie potentielle élastique est nulle à z=0, mais cela n'a pas d'impact sur la réponse à la question posée.]
Ensuite, on nous demande de déduire la constante du ressort, K, à partir des données. Comme il y a seulement le poids et la force de rappel du ressort, l'évolution est conservative, c'est-à-dire que l'énergie mécanique est constante. Nous pouvons donc examiner ce qui se passe avant de lancer la fléchette et à l'altitude maximale.
Avant de lancer la fléchette, nous connaissons L1-L0 (soit -6 cm). L'énergie potentielle élastique est donc donnée, et l'énergie cinétique est nulle car la fléchette n'a pas encore de vitesse. À l'altitude maximale, l'énergie potentielle élastique est nulle (car le terme s'annule) et l'énergie potentielle de pesanteur est mgh. De plus, la vitesse est nulle à l'altitude maximale.
En utilisant le fait que l'énergie mécanique est constante (em1=em2), nous pouvons établir l'équation 1/2 * k * (L1-L0)² = mgh. En résolvant cette équation, nous trouvons que k = 2mgh / (L1-L0)², soit 1000 N/m avec les valeurs numériques fournies dans l'exercice.
N'oubliez pas d'inclure les unités lors de l'application numérique, sinon vous risquez d'obtenir une réponse incorrecte. J'espère que cela vous a été utile, n'hésitez pas à poser vos questions dans les commentaires.