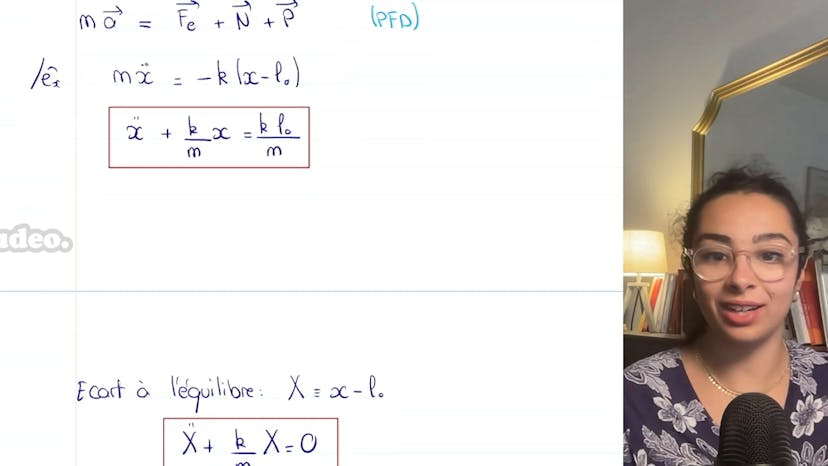Home

MPSI/PCSI

Physique-Chimie

Physique

Mécanique vibratoire

Dans cet exercice, nous étudions les oscillateurs harmoniques non amortis. Nous nous intéressons spécifiquement à un système masse-ressort vertical, en négligeant la poussée d'Archimède et les frottements. Tout d'abord, nous faisons un bilan des forces qui agissent sur la masse m. Les forces incluent le poids dirigé vers le bas (mgex) et la force de rappel du ressort (kx-l0ex). Nous vérifions que la force de rappel ramène le ressort vers sa position d'équilibre lorsqu'il est étiré. Ensuite, nous déterminons l'équation différentielle en utilisant le principe fondamental de la dynamique projetée sur ux. Nous obtenons mx² = mgex-kx-l0. Lorsqu'il atteint la position d'équilibre, les forces se compensent, ce qui donne mg-kx-l0 = 0. La position d'équilibre est ainsi donnée par xex = l0 + mg/k. Cette relation montre que plus la masse est grande, plus la position d'équilibre est basse par rapport à l0. L'équation différentielle vérifiée par x en fonction de x, xex, m et k est transformée en une forme plus simple en introduisant l'écart à la position d'équilibre (x - xex). L'équation devient x seconde + ω0²x = 0, avec ω0² = k/m. Nous pouvons alors déterminer la période du mouvement, t0 = 1/(2π√(m/k)). Enfin, nous résolvons l'équation en prenant en compte les conditions initiales où la masse est à l'équilibre (x = 0) mais possède une vitesse v0 dirigée vers le bas (x = v0). La solution générale est donnée par x(t) = v0/ω0 sin(ωt). Cette résolution inclut les étapes classiques pour ce type d'exercice, notamment l'application du principe fondamental de la dynamique, le changement de variable et la résolution de l'équation différentielle.

Bonjour à tous, on se retrouve aujourd'hui pour faire un exercice sur les oscillateurs harmoniques non amortis. Donc on a déjà fait ensemble le cas du système masse-ressort horizontal. Ici on se retrouve avec un système masse-ressort qui est vertical. On vous dit qu'on néglige la poussée d'archimède dans l'air, donc les frottements, et on étudie en fait ce ressort-là vertical. Première question qu'on nous pose ici, c'est de faire un bilan des forces qui s'exercent sur la masse m. Donc le bilan des forces, c'est toujours la même chose. J'ai deux forces ici, j'ai le poids qui est vers le bas, qui est donc mgex, et la force de rappel qui est kx-l0ex. Donc je vérifie bien toujours quand j'ai une force comme ça, une force de rappel, je vérifie bien que lorsque j'étire le ressort, la force a bien tendance à le ramener vers sa position d'équilibre. C'est bête, c'est des erreurs de signes, mais parfois ça peut quand même être fatal dans ce type d'exercice. Donc maintenant, ensuite on nous demande de déterminer l'équation différentielle, donc je prends le principe fondamental de la dynamique que je projette sur ux, je vais aller un peu vite ici parce que c'est des choses qu'on a déjà faites, et ça me donne mx² est égal à mgex-kx-l0. Maintenant pour la position d'équilibre, si je suis à l'équilibre, ça veut dire que la somme des forces qui s'exercent sur la bille est nulle, donc dans ces cas-là, je peux remplacer ça par juste la somme des forces est nulle, ou sinon je peux aussi prendre le principe fondamental de la dynamique et regarder à quel moment l'accélération est nulle. Et donc dans ces cas-là, je suis à la position d'équilibre aussi. Et donc là, ça me donne mg-kx-l0 est égal à 0, donc xex est égal à l0 plus mg sur k. Et c'est assez logique, ça veut dire que plus ma bille est lourde, plus en fait la position d'équilibre est basse par rapport à l0, donc ça c'est assez logique. On retrouve bien évidemment, le plus important c'est de raccorder les deux cas ensemble. Si on met le ressort horizontal ou si on imagine qu'on a une masse nulle, on retrouve bien xex est égal à l0. Maintenant question 4, équation différentielle vérifiée par x en fonction de x, xex, m et k. Donc là, ça demande juste de changer un peu la forme de l'équation différentielle. C'est ce qu'on a déjà fait en fait, c'est que c'est plus simple de repérer les mouvements du ressort par rapport à x, qui est égal à x moins xex, qui est en fait l'écart à la position d'équilibre. Là, je vois apparaître ici ce xex fois k sur m, donc ça me permet de mettre l'équation sous la forme d'un oscillateur harmonique, x seconde plus omega0 carré x est égal à 0. Et ici, j'ai toujours la même pulsation propre, c'est omega0 est égal à k sur m. Donc vous voyez, le plus simple en fait, je pense, quand on a ce genre d'expression, c'est de voir apparaître xex quelque part. Donc là, je vois ici qu'il apparaît plus ou moins. Ensuite pour la période, donc omega0 c'est racine de k sur m, omega0 c'est 2pi sur t0, et donc j'ai t0 est égal à 1 sur 2pi racine de m sur k. Finalement, on demande de résoudre cette équation. On nous dit qu'au début, on lui communique une vitesse v0 vers le bas, donc selon x, et que la masse est à l'équilibre. Donc on a grand x qui est égal à 0. Donc voilà la forme de la solution. Moi ici, j'ai préféré la forme cosinus plus sinus en combinaison linéaire, mais vous pouvez s'y mettre sous la forme acos omega t plus phi. x de 0 c'est 0, donc on est à l'équilibre, et on communique une vitesse qui est vers ex, donc x.20 c'est v0. Donc comme ça, si j'injecte, je vois que x de 0 c'est a, et x.20, vous voyez ici, je dérive le sinus, donc ça va être omega0 b, et donc ça me donne a égale 0 et b égale v0 sur omega0. Finalement, j'ai l'expression définitive x de t qui est égale à v0 sur omega0 sinus de omega t. Vous voyez, dans cet exercice, on a fait vraiment tout ce qui est ultra classique. On a déjà fait pour le système masse ressort horizontal. Tout d'abord, on a appliqué le principe fondamental de la dynamique pour déterminer l'équation du mouvement. Chose importante, on a fait un petit changement de variable pour le mettre sous la forme d'un écart à la position d'équilibre. Et finalement, on a résolu l'équation différentielle.

Oscillations non-amorties

RELATED

Recommended videos

Masse-ressort

Oscillateur harmonique

Pendule simple