Home

Terminale

Maths Spé

Analyse

Convexité

Ce cours porte sur la convexité des fonctions et les points d'inflexion. La fonction étudiée est f2x et nous allons la dériver deux fois pour trouver ses variations. 

Nous commençons par calculer la première dérivée, f', qui est toujours positive car l'exponentielle dans la fonction est positive. Le signe important est celui de "-x plus 1". Ce terme est positif pour x allant de moins l'infini à 1 et négatif sinon. Nous en déduisons que la dérivée est positive pour x < 1 et négative pour x > 1. 

En utilisant ces informations, nous construisons le tableau de variations de la fonction f. Elle est croissante jusqu'à x = 1, puis décroissante. Son maximum est atteint à x = 1, avec une valeur de 7e-1. 

Nous calculons également les limites de la fonction aux infinis. Pour x tendant vers moins l'infini, la limite est moins l'infini, tandis que pour x tendant vers plus l'infini, la limite est 0. Nous avons ainsi un tableau de variations complet.

Ensuite, nous calculons la seconde dérivée, f'' qui est également dérivable. Le résultat final est 7 fois x moins 2, fois e de moins x. Comme l'exponentielle est positive, le signe dépend de x moins 2. La dérivée est positive pour x > 2 et négative pour x < 2. Nous concluons que la dérivée seconde change de signe en x = 2, ce qui indique un point d'inflexion.

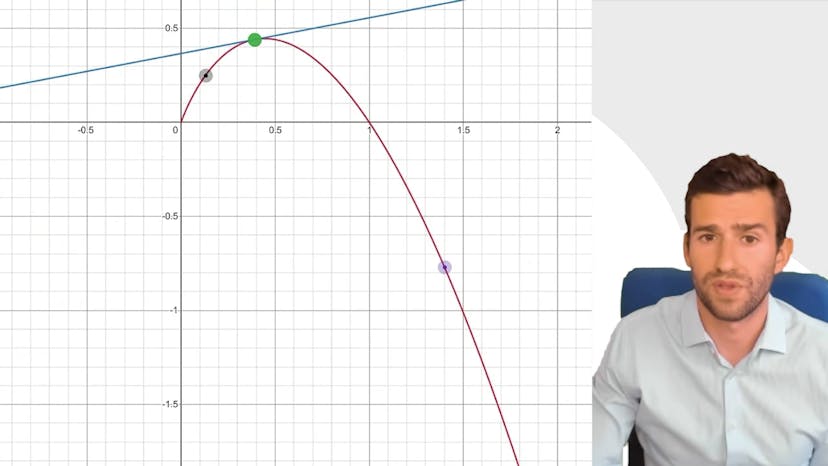
Pour trouver les coordonnées de ce point d'inflexion, nous évaluons f(2) qui est égal à 14 moins 2, soit 12. Visuellement, sur le graphique de la fonction, on peut observer que la pente diminue avant le point d'inflexion, puis commence à augmenter après. La courbe de la dérivée seconde confirme cette observation.

Les points d'inflexion sont couramment utilisés en physique, notamment dans le titrage pour repérer un changement d'augmentation ou de diminution de la pente de la courbe. Cela conclut notre étude sur la convexité et les points d'inflexion.

N'hésitez pas à consulter la FAQ si vous avez d'autres questions.

Encore une méthode sur la convexité, c'est la dernière, sachant que dans celle-ci on va voir aussi les points d'inflexion qui peuvent nous être utiles selon les questions posées. On va étudier la fonction f2x qui est la suivante. Maintenant vous commencez à avoir l'habitude, ce qu'on va faire c'est qu'on va la dériver deux fois. On justifie toujours qu'elle est bien dérivable deux fois, pas de problème, c'est des produits de fonctions dérivables deux fois. Donc je calcule f', il y a une erreur dans l'énoncé, en déduisant les variations de f ce n'est pas avec f2, c'est avec f'. Là ce qu'on me demande c'est bien f', donc je calcule f'. Je vois que là j'ai une exponentielle, c'est toujours positif, n'oublions pas, donc là je n'ai aucun problème sur le signe, même s'il y a un "-x dedans", évidemment une exponentielle c'est positif, on ne répétera jamais assez, positif, une exponentielle, positif. Ce qui est important c'est le signe du "-x plus 1", donc ce "-x plus 1", il est positif pour x allant de moins l'infini à 1 et négatif sinon. J'en déduis le signe de la dérivée, qui est positif sur "-x plus 1", qui est négatif sur 1 plus l'infini. J'en déduis le tableau de variation de f, la fonction f est croissante puis décroissante avec un maximum atteint 1, dont j'ai calculé la valeur qui vaut 7e de moins 1. Pour faire un tableau de variation propre, on calcule les limites, donc en moins l'infini, là aucun problème, parce que ça fait moins l'infini, ou plus l'infini, ici, sur les opérations sur les limites, ça fait moins l'infini. En plus l'infini c'est un tout petit peu plus subtil, je vais utiliser mes limites de référence avec la croissance comparée, je sais que e de x sur x tend vers 0, et donc e de moins x est 1 sur e de x, donc je peux l'écrire x sur e de x, et c'est l'inverse de 2x sur x, donc ça tend vers 0 en plus l'infini, donc ma limite c'est 0. Là j'ai fait un tableau de variation complet, j'ai mes limites et la valeur maximum. Ensuite, on me demande de calculer f seconde de x, je redirais une deuxième fois, il n'y a pas de problème, c'est encore une fois un produit de polynômes qui sont dérivables, donc c'est bon. Je trouve à la fin, en faisant le calcul, 7 fois x moins 2, fois e de moins x. Idem, l'exponentiel est toujours positif, donc c'est du signe de x moins 2, et donc c'est positif pour x supérieur à 2, et négatif pour x inférieur à 2. Donc, f seconde change de signe en x égale 2, et quand on a un changement de signe de la dérivée seconde, c'est donc un point d'inflexion. Donc le point x égale 2, c'est un point d'inflexion, pour voir les coordonnées, de ce point d'inflexion c'est 2 f de 2, et donc si je fais le calcul, la valeur exacte de f de 2, ça fait 14 de 2 moins 2. Et sur la courbe, comment ça se voit, donc ça c'est la courbe de CF, en fait, un point d'inflexion, vous pouvez le voir, c'est comme, avant le point d'inflexion, on voit que la pente diminue, diminue, diminue, jusqu'à ce qu'elle soit nulle, elle continue à diminuer, diminuer, diminuer, jusqu'à ce point là, où là, elle arrête de diminuer, maintenant, elle a tendance à augmenter, c'est à dire à s'incurver, pour remonter. Elle va devenir de moins en moins négative, et passer éventuellement au positif, là c'est pas le cas. Donc voilà, et donc si on trace justement la courbe de CF seconde, la courbe de CEP seconde, on voit bien là qu'elle est négative d'abord, donc là j'ai une dérivée seconde qui est négative, qui est négative, et elle change de signe en 2. Donc voilà, donc là on a bien un point d'inflexion, visuellement ça se voit, où est-ce que vous avez souvent vu des points d'inflexion, pour ceux qui font de la physique, c'est quand vous faites un titrage par exemple, vous faites un titrage, en ph, etc, vous avez une courbe du type un truc comme ça, et on repère le point d'inflexion qui est ici au milieu. Donc vous avez l'habitude de repérer un point d'inflexion, c'est là où on a un changement d'augmentation, de diminution de la pente. Voilà donc pour cette méthode sur la convexité et sur les points d'inflexion, dernière thématique qu'on a traité sur toutes ces méthodes. Voilà, s'il y avait des questions, n'hésitez pas à aller voir la FAQ.

Points d'Inflexion

RELATED

Recommended videos

Convexité et f''

Convexité et Inégalités