Online Maths Courses by Top Instructors

Relations coéfficients racines

Dans ce cours, le professeur explique qu'il y a un nouveau problème à résoudre sur les polynômes de degré 2. L'équation x²-x-9 a deux solutions x' et x''. L'objectif est de trouver les expressions suivantes sans les calculer : la somme du carré des deux solutions et la différence des deux au carré. Le professeur rappelle qu'il faut trouver des relations entre les racines et les coefficients au lieu de les calculer. Il explique que la somme des racines est égale au coefficient devant x avec un signe moins (-b/a) et le produit des racines est égal au terme constant (-c/a). Il suggère d'utiliser les identités remarquables pour résoudre le problème. En utilisant l'identité remarquable (a+b)² = a² + b² + 2ab, il développe l'expression (x' + x'')² et obtient x'² + x''² + 2x'x'' = 1. En utilisant le terme constant du polynôme (-c/a) = (-9/1) = -9, il trouve que x'² + x''² = 19. Ensuite, il développe l'expression (x' - x'')² et obtient x'² + x''² - 2x'x'' = 37. Il conclut en soulignant l'importance de trouver les bonnes relations et l'utilisation des identités remarquables pour résoudre le problème sans calculer les racines.

Position relative parabole et droite

Dans cet exercice, nous étudions les positions de deux courbes : une parabole (représentée par la fonction f) et une droite (représentée par la fonction g). La méthode consiste à trouver la différence entre les expressions des deux courbes (f2x - g2x) et à déterminer quand cette différence est positive ou négative. Nous avons d'abord la question initiale qui nous rappelle la méthode : nous devons étudier la différence entre les expressions des deux courbes (f2x - g2x) et déterminer quand elle est positive ou négative. Ensuite, nous évaluons cette différence en utilisant les équations de la parabole et de la droite. Nous obtenons 2x² - 3x + 5 - 5x + 3 = 2x² - 8x + 8. Nous factorisons cette expression par 2 et obtenons x² - 4x + 4, qui est une identité remarquable bien connue (2x - 2)². Nous en déduisons que f est toujours au-dessus de g quel que soit x appartenant à R. En d'autres termes, cf (courbe représentative de f) est toujours au-dessus de cg (courbe représentative de g). Nous pouvons conclure que f et g sont tangentes en x = 2, car f(2) = g(2) et f(2)² = g(2)². Pour vérifier nos conclusions, nous traçons les courbes sur une calculatrice graphique. Nous observons qu'il y a un point de tangence où les courbes se touchent, à x = 2. Par ailleurs, en zoomant, nous constatons que la parabole rouge reste toujours au-dessus de la droite bleue. En résumé, cet exercice consiste à étudier les positions de deux courbes (une parabole et une droite) en comparant leurs expressions. Nous déterminons que ces courbes sont tangentes en x = 2 et que la parabole est toujours au-dessus de la droite.

Rencontre entre parabole et droite

Ce cours porte sur l'intersection entre une parabole et des droites verticales ou horizontales. En déplaçant la valeur de la droite verticale, on observe que les points d'intersection varient. De même, lorsqu'une droite horizontale croise la parabole, il peut y avoir un point de tangence ou deux points d'intersection. Pour déterminer le nombre de points d'intersection entre les droites x=k et la parabole 4x²-8x+7, on résout l'équation en remplaçant y par 4k²-8k+7. On trouve ainsi un unique point d'intersection (k, 4k²-8k+7). Si la droite horizontale est de la forme y=k, on distingue les cas selon les valeurs de k. Si k<3, il n'y a pas d'intersection. Si k=3, il y a un point de tangence. Si k>3, il y a deux points d'intersection, dont les coordonnées peuvent être calculées en utilisant le discriminant. En résumé, il faut faire attention au signe du discriminant pour déterminer le nombre de points d'intersection.

Calcul de termes arithmétiques

Ce cours explique la méthode fondamentale des suites arithmétiques et fournit des exemples. Une suite arithmétique est une suite où chaque terme est la somme du terme précédent et d'une constante appelée raison. Pour trouver un terme, il suffit d'ajouter la raison au terme précédent.Dans un exemple, on voit qu'une suite arithmétique a une raison de -4 et que le premier terme est 3. On peut alors calculer le deuxième terme en soustrayant 4 de 3, obtenant ainsi -1. Un autre exemple est donné avec une suite arithmétique où le quatrième terme est 5 et la raison est 5. On doit ajouter la raison 6 fois pour arriver au terme numéro 10. En utilisant cela, on peut trouver directement que le terme numéro 10 est égal au quatrième terme plus 6 fois la raison. Dans cet exemple, cela donne 5 plus 30, soit 35. C'est une méthode simple pour trouver n'importe quel terme dans une suite arithmétique en connaissant la raison et un ou plusieurs termes.

Calcul de termes géométriques

Ce cours explique la méthode fondamentale pour les suites géométriques. Il démarre par une question sur la suite géométrique de raison 3 avec U6 égal à 5 et demande de calculer U20. Pour passer d'un terme à l'autre, il suffit de multiplier le terme précédent par la raison. Ainsi, pour passer de U6 à U20, il faut multiplier U6 par 3 puissance (20-6), ce qui donne la réponse. La deuxième question concerne une suite géométrique de raison 2 et le premier terme est -6. La formule de la suite géométrique donne Vn = V0 fois la raison puissance n. Donc ici, Vn est égal à -6 fois 2 puissance n. La méthode principale à retenir est de comprendre qu'on peut sauter directement entre les termes en calculant la différence entre eux, comme dans le premier exemple.

Expression de termes d'une suite explicite

Une suite est une fonction qui prend comme antécédent l'ensemble des entiers naturels. Au lieu d'écrire "f de x", on peut écrire "u de n" ou "u indice n". Pour illustrer cela, prenons un exemple : définissons une fonction où pour tout entier naturel n, u égal au carré de n plus 1. Ainsi, si l'on considère u de 3, l'image de l'antécédent 3 par u sera 10. Pour exprimer différentes expressions, reprenons l'expression de u et considérons-la comme u de quelque chose. Ainsi, u de quelque chose sera "chose au carré plus 1". En prenant "chose" égal à "n plus 1", l'expression reste la même et devient "n plus 1 au carré plus 1". De même, pour u suivant, avec "chose" égal à "n moins 1", l'expression devient "n moins 1 au carré plus 1". Pour u de z, l'expression reste toujours la même, c'est-à-dire "2z". Enfin, pour u indice n plus 1, l'expression est "n carré plus 2". Il est important de faire attention aux nuances et de ne pas confondre les expressions comme "un plus 1" où "n plus 1" est l'antécédent, et "un plus 1" où l'on ajoute simplement 1 à un.

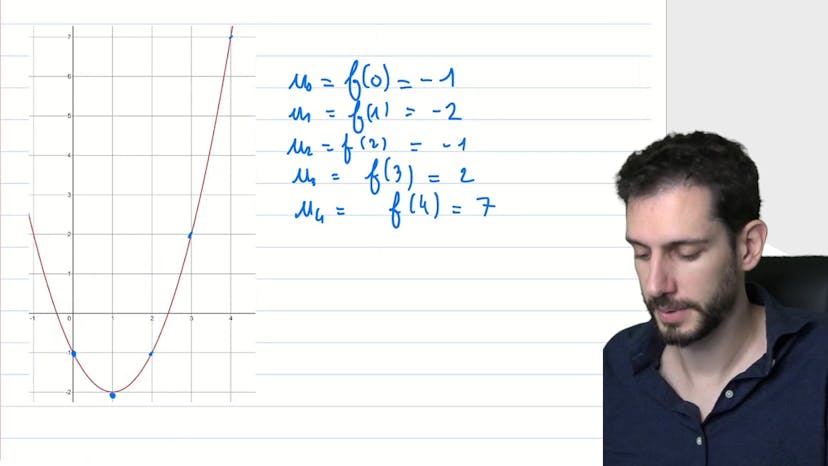
Lire des termes d'une suite explicite

Dans cette vidéo, nous traitons du lien entre une suite explicite et la représentation générale d'une fonction. Lorsque nous définissons explicitement une suite, nous ne considérons que certains antécédents et images d'une fonction définie sur R. Par exemple, la suite f2n est définie uniquement pour les entiers naturels, tels que n=0,1,2,3,4,5,6,7, et ainsi de suite. Pour déterminer les cinq premiers termes de la suite, nous recherchons f2 0, f2 1, f2 2, f2 3 et f2 4 sur le graphique. En lisant les coordonnées correspondantes sur le graphique, nous trouvons que u0 = f2 0 = -1, u1 = f2 1 = -2, u2 = f2 2 = -1, u3 = f2 3 = 2 et u4 = f2 4 = 7. Ainsi, la fonction associée à la suite peut prendre des valeurs négatives ou positives. Par exemple, la suite vn = racine de n + 2 peut donner des valeurs qui ne sont ni entiers naturels ni entiers relatifs. En résumé, une suite est une représentation discrète de points choisis à partir d'une fonction définie sur un ensemble de règles.

Application type des suites géométriques

Cet article explique l'utilisation des suites pour suivre l'évolution de données économiques ou démographiques. Le texte donne un exemple de ville qui a augmenté de 10% chaque année depuis 2018, pour montrer comment les suites peuvent être utilisées pour tracer ces évolutions. Le texte explique comment chaque terme de la suite peut être calculé, et justifie que cette suite est en réalité géométrique plutôt qu'arithmétique. Il explique également comment la raison de la suite peut être trouvée, et fournit des formules pour calculer chaque terme.

Somme de termes d'une suite arithmétique

Dans ce cours, nous calculons la somme des 25 premiers entiers naturels pairs. Pour résoudre cet exercice classique, nous utilisons nos connaissances sur les suites arithmétiques et géométriques, ainsi que sur les formules pour les sommes de termes de ces suites. Nous identifions rapidement que la somme est une suite arithmétique de raison 2. Nous écrivons la suite sous forme de combien de fois 2 chaque nombre est égal, en sachant que le 25ème terme est 24 fois 2 et non pas 25 fois 2. Nous appliquons la formule de la somme des n premiers entiers pour obtenir le résultat final : 300.

Somme de termes d'une suite géométrique

Dans cet exercice de mathématiques, il est demandé de calculer deux sommes. La première est une somme de termes d'une suite arithmétique et peut être résolue avec la formule générale où S est égal à 1 moins Q puissance le nombre de termes sur 1 moins Q. Dans cet exemple, Q est égal à 3 et le nombre de termes est 12. La deuxième somme est une somme de termes d'une suite géométrique, cependant, les termes ne sont pas donnés sous forme de puissance. En observant les alternances de signes, il est facile de comprendre que la raison est -2 et que le dernier terme est -2048. La formule générale est appliquée avec Q étant -2 et le nombre de termes étant 11. La somme finale est obtenue après des calculs mentaux simples.

Variations d'une suite - un peu bizarre !

Ce cours se concentre sur l'étude des variations de suites. La méthode principale est de calculer la différence entre deux termes successifs, soit un plus un moins un. Si le résultat est positif, cela signifie que le terme suivant est plus grand, et donc la suite est croissante. Si le résultat est négatif, cela signifie que le terme suivant est plus petit, et donc la suite est décroissante. Dans cet exemple particulier, la suite est définie par u0 = 3 et un+1 = un + 1. En calculant un plus un moins un, on obtient un plus la racine carrée de n. Cette expression est positive ou nulle, ce qui signifie que la suite est croissante. Dans un autre exercice, on cherche à déterminer la croissance de la suite vn+1 = 3/vn. En calculant vn plus un moins vn, on obtient 3 - vn^2 / vn. Dans ce cas, il n'est pas évident de trouver un résultat immédiatement. Donc, il est conseillé de calculer quelques termes de la suite pour avoir une idée de la croissance. En calculant les premiers termes, on remarque que la suite oscille entre les valeurs 1 et 3, et donc n'est ni croissante ni décroissante. Il est important de ne pas paniquer lorsque l'on rencontre des difficultés dans la conclusion d'un problème. Calculer quelques termes de la suite peut souvent aider à se débloquer.