Online Révisions Maths lycée Courses by Top Instructors

Analyse Terminale

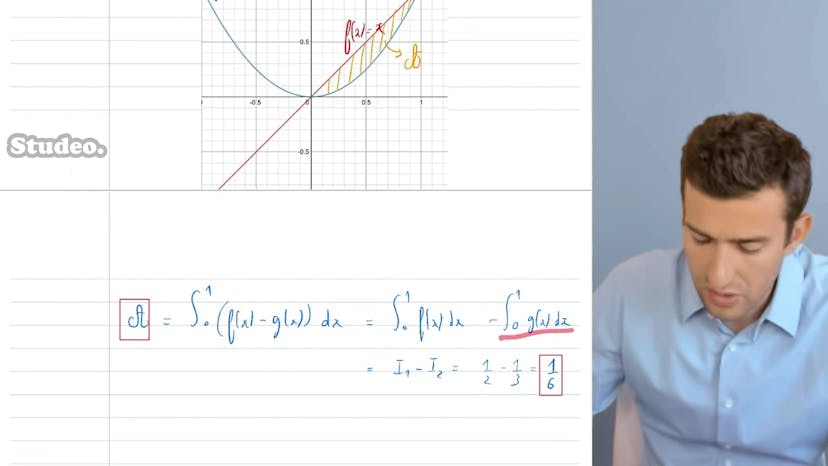
Aire entre 2 Courbes

Dans ce cours, nous apprenons comment calculer l'R entre deux courbes, f(x) = x et g(x) = x², sur l'intervalle de x = 0 à x = 1. Pour calculer l'R, nous devons d'abord trouver les primitives des deux fonctions f et g. La primitive de f(x) = x est F(x) = x²/2, et la primitive de g(x) = x² est G(x) = x³/3. En utilisant le théorème fondamental du calcul, l'R se situe entre les courbes f et g, et peut être calculée en trouvant la différence entre les intégrales de f(x) et g(x) sur l'intervalle de x = 0 à x = 1. Dans ce cas, la fonction f(x) est toujours supérieure à la fonction g(x) sur l'intervalle de 0 à 1. Donc, nous calculons l'intégrale de f(x) - g(x), ce qui équivaut à l'intégrale de 0 à 1 de f(x) moins l'intégrale de 0 à 1 de g(x). En utilisant les primitives que nous avons trouvées, nous évaluons les intégrales et obtenons les valeurs I1 et I2. I1 est égal à 1/2 et I2 est égal à 1/3. Donc, la différence entre I1 et I2 est égale à 1/2 - 1/3, ce qui donne 1/6. Ainsi, l'R entre les courbes f(x) et g(x) sur l'intervalle de 0 à 1 est égale à 1/6. C'est ainsi que l'on calcule l'R entre deux courbes.

Analyse Terminale

Calcul Valeur Moyenne

Le cours explique comment calculer la valeur moyenne d'une fonction à partir de deux exemples : la fonction f et la fonction g, avec des intervalles différents. La valeur moyenne est définie comme l'intégrale de la fonction sur l'intervalle divisée par la largeur de l'intervalle. Pour trouver cette valeur moyenne, on doit trouver une primitive de la fonction intégrale. Dans le premier exemple, on pose h égale à x² plus 3, et on utilise le théorème fondamental pour trouver que la valeur moyenne est de 13 tiers. Dans le deuxième exemple, on veut la valeur moyenne de g, qui est x sur x²-3. On remarque que c'est un quotient et on l'écrit comme u' sur u. On trouve que la primitive de g est un demi de ln de la valeur absolue de x²-3. On intègre cette fonction sur l'intervalle de e à 4 en se débarrassant de la valeur absolue. On obtient une expression avec des ln, et on simplifie si possible. Finalement, on conclut que le calcul de la valeur moyenne d'une fonction revient à faire un simple calcul d'intégrale.

Analyse Terminale

Suite d'Intégrales

Une méthode pour étudier la convergence d'une suite d'intégrales est présentée dans cette transcription de vidéo. On nous donne une suite de fonctions qui vaut 1 plus t à la puissance n, et on cherche à trouver sa convergence. La première méthode consiste à encadrer cette fonction entre 1 et 1 moins t à la puissance n. On construit des inégalités en utilisant les propriétés des fonctions croissantes et décroissantes. Cependant, cette méthode ne fonctionne pas pour la deuxième inégalité. Donc, on utilise une deuxième méthode plus instinctive, qui consiste à faire la différence entre les deux termes de l'inégalité. On met tout au même dénominateur et on simplifie pour montrer que cette expression est positive. Ainsi, on conclut que 1 moins t à la puissance n est plus petit que 1 sur 1 plus t à la puissance n. Ensuite, on calcule l'intégrale de 1 moins t à la puissance n de 0 à 1 en utilisant la linéarité de l'intégrale. On trouve que cette intégrale est égale à n sur n plus 1. En utilisant l'encadrement précédemment obtenu, on déduit un encadrement pour l'intégrale im. On montre ensuite que la suite im converge vers 1 en utilisant le théorème d'encadrement.

Trouver un angle avec le produit scalaire

Le cours traite du calcul de l'angle entre les diagonales AG et OF dans un cube d'arête 1. L'approche utilisée est basée sur le produit scalaire. En utilisant les coordonnées des points du cube, le professeur représente le cube comme un espace en trois dimensions et attribue des vecteurs unitaires aux côtés du cube. Ensuite, il calcule les coordonnées des points D, G et F, qui sont les points d'intérêt pour le calcul de l'angle. Les coordonnées de D sont (0,1,0), celles de G sont (1,1,1) et celles de F sont (1,0,1). Ensuite, le professeur calcule les vecteurs AG et DF, qui sont respectivement (1,1,1) et (1,-1,1). Il calcule également les normes de ces vecteurs, qui sont toutes deux racine de 3. En utilisant ces valeurs, le professeur forme une équation pour trouver le cosinus de l'angle FOG en utilisant la formule du produit scalaire. En faisant les calculs, il obtient un cosinus égal à 1/3. En arrondissant l'angle à 0,01 degré près, le professeur obtient un angle de 70,53 degrés. L'approche utilisée, qui consiste à utiliser les coordonnées et à poser un repère, permet d'obtenir des résultats efficacement. Il est donc recommandé de prendre l'initiative d'utiliser cette méthode pour résoudre ce type d'exercice en géométrie.

Méthode classique de géométrie dans l'espace

Ce cours porte sur la géométrie dans l'espace et présente un exercice classique à résoudre. Dans cet exercice, ABCD et FGH représentent un cube de côté A. Le point M est le milieu du segment AB. Pour montrer que le triangle DHM est rectangle, on observe que DH est un vecteur normal pour le plan ABC, c'est-à-dire la face inférieure du cube. Ensuite, pour déterminer la valeur de l'angle DMH en degrés arrondi à 0,01 près, on peut calculer le produit entre les vecteurs MH et MD, mais il est plus simple de remarquer que le triangle est rectangle. On peut donc utiliser les propriétés du triangle rectangle et dire que l'hypoténuse est HM. On peut alors calculer la longueur DM et utiliser la formule de la tangente pour trouver l'angle recherché. Peu importe la mesure du côté du cube, l'angle entre les points H, M et D reste le même. Ainsi, la longueur du côté n'intervient pas dans l'expression de l'angle. En calculant la tangente inverse (ou arctangente) de DH/DM, on obtient la valeur de l'angle recherché.

Distance d'un point à un plan

Le cours traite de la méthode classique pour déterminer la distance entre un point et un plan dans l'espace. La distance minimale entre le point et le plan est appelée distance entre un point et un plan. La distance minimale est obtenue en effectuant une projection orthogonale du point sur le plan. Une formule, souvent apprise par cœur, permet de calculer cette distance. Elle utilise les coordonnées du point et un vecteur normal au plan. Dans le cours, un exemple est donné pour illustrer le calcul de la distance entre un point et un plan en utilisant cette formule. Le point C est donné, ainsi qu'un vecteur normal au plan. En utilisant les coordonnées du point et le vecteur normal, on peut exprimer les coordonnées du point H, qui est le projeté orthogonal du point C sur le plan. La distance entre le point C et le plan est ensuite calculée en utilisant la norme du vecteur résultant. La formule détaillée ainsi que les calculs sont expliqués pas à pas dans le cours.

Distance entre deux droites non coplanaires

Dans cet exercice, nous devons trouver une équation paramétrique pour deux droites données, montrer qu'elles ne sont pas coplanaires et vérifier que certains points appartiennent à ces droites. Ensuite, nous devons démontrer que HK est la perpendiculaire commune entre ces deux droites et calculer la distance entre elles. Tout d'abord, nous avons un point et un vecteur directeur pour chaque droite, ce qui nous permet de trouver une équation paramétrique basique pour chaque droite. Ensuite, nous devons démontrer qu'elles ne sont pas coplanaires, c'est-à-dire qu'elles ne sont ni parallèles ni avec aucun point d'intersection. Nous utilisons un raisonnement par l'absurde pour montrer qu'il n'est pas possible de trouver des valeurs cohérentes pour les paramètres dans les équations des deux droites. Ensuite, nous vérifions que certains points appartiennent à ces droites en résolvant les équations paramétriques pour trouver les valeurs des paramètres correspondants. Ensuite, nous montrons que HK est la perpendiculaire commune en vérifiant que les vecteurs directeurs des droites sont orthogonaux à HK. Enfin, la distance entre les droites est définie comme la distance entre les points H et K, que nous calculons en utilisant la norme du vecteur HK. Cet exercice nécessite un dessin pour mieux comprendre et une bonne compréhension des concepts de droites paramétriques, de coplanarité et d'orthogonalité.

Trouver l'équation d'un plan avec un vecteur normal

Dans ce cours, on aborde la notion de plan dans l'espace. Pour vérifier si trois points (A, B, C) définissent un plan, il faut s'assurer qu'ils ne sont pas alignés. On peut le faire en vérifiant si les vecteurs formés par ces points sont collinéaires ou non. Pour illustrer, on propose de calculer le vecteur AB. On constate qu'il est différent du vecteur AC, ce qui signifie que les points ne sont pas alignés. Ensuite, on explique qu'il est possible de se perdre dans des fausses pistes lors de l'étude de la géométrie, mais il est préférable de connaître plusieurs exercices par cœur pour pouvoir reconnaître rapidement les bonnes pistes. Ensuite, on aborde la manière de déterminer une équation cartésienne du plan ABC. Pour cela, on cherche d'abord le vecteur normal au plan, en utilisant les produits scalaires entre ce vecteur et les vecteurs A, B et A, C. On obtient ainsi deux équations pour les trois inconnues (A, B, C). Cela signifie qu'il existe une infinité de vecteurs normaux possibles, et on peut choisir celui qui convient le mieux. En résolvant les équations, on trouve que B est égal à 0. Ainsi, le vecteur normal peut être choisi comme étant (0, A, 0). On explique alors que l'équation cartésienne du plan peut être formulée comme 1x + Ay + 1z = 0. En conclusion, on explique qu'il est possible de trouver l'équation cartésienne d'un plan en deux étapes. D'abord, on cherche un vecteur normal en utilisant les produits scalaires. Ensuite, on utilise ce vecteur normal pour trouver rapidement l'équation cartésienne.

Trouver un plan avec 3 points

Le cours explique comment trouver l'équation cartésienne d'un plan passant par un point donné avec un vecteur normal donné. Il présente deux méthodes pour cela. La première méthode consiste à utiliser l'équation générale du plan, qui est de la forme ax + by + cz + d = 0, en utilisant les coordonnées du vecteur normal (abc). Cette méthode est utilisée de manière pratique sans démonstration. La deuxième méthode est préférée par l'auteur car elle repose sur une démonstration plus complète. Elle utilise le concept de vecteur normal orthogonal au plan. Un point M appartiendra au plan si et seulement si le vecteur GM est orthogonal au vecteur normal. En utilisant cette propriété, on peut écrire l'équation du plan en utilisant le produit scalaire entre le vecteur GM et le vecteur normal. Cette équation donne les mêmes résultats que la première méthode. L'auteur souligne l'importance de comprendre la définition profonde d'un vecteur normal, qui est d'être orthogonal à tous les vecteurs du plan.

Probas Terminale

Cours par cas pratiques !

Lors de ce cours, nous traitons de la détermination du nombre d'anagrammes, c'est-à-dire le nombre de façons de combiner les lettres d'un mot. Pour calculer ce nombre, nous utilisons la notion de permutation, qui correspond au nombre de choix possibles pour ranger les lettres dans des cases. Par exemple, pour le mot ABC, il y a 3! (3 factorielle) façons de l'organiser, car il y a 3 lettres et 3 cases. De même, pour les mots CHA, CHIEN et VALISE, nous utilisons respectivement 3!, 4!, 5! et 6! pour déterminer leur nombre d'anagrammes. Ensuite, nous abordons des mots avec des lettres répétées, comme AXA. Dans ce cas, nous devons prendre en compte le fait que les lettres identiques ne peuvent pas être distinguées. Par exemple, pour AXA, nous aurons seulement 3 choix possibles (AAX, AXA, XAA) au lieu de 6, car les deux lettres A peuvent être permutées entre elles. Ainsi, pour chaque combinaison de lettres, nous devons diviser par le nombre de permutations possibles des lettres identiques. Nous généralisons ensuite ce raisonnement pour des mots plus complexes tels que "visir" et "abracadabra". Pour ces mots, nous prenons en compte le nombre de lettres répétées (par exemple, 2 a dans "abracadabra") et le nombre de permutations possibles pour chaque lettre. Nous calculons donc le nombre d'anagrammes en utilisant le nombre total de lettres et en divisant par le produit des facteurs correspondant aux lettres répétées. En conclusion, le calcul du nombre d'anagrammes peut être complexe, mais en utilisant les principes de permutation et en prenant en compte les lettres répétées, nous pouvons obtenir des résultats précis. Cela nous permet de comprendre et de déterminer le nombre de combinaisons possibles pour des mots donnés.

Probas Terminale

Déterminer des ensembles

Dans ce cours sur le dénombrement, on va traiter des ensembles et des listes. Un ensemble est comme un sac qui contient des objets, sans ordre spécifique. Une liste, en revanche, est une séquence d'objets avec un ordre précis. Les ensembles peuvent contenir d'autres ensembles, tandis que les listes représentent des coordonnées (ex: 1-2 n'est pas la même chose que 2-1). Lorsqu'on aborde des problèmes où l'ordre compte, on travaille avec des listes, sinon on utilise des ensembles et les combinatoires. Dans l'exemple donné, on a deux ensembles E et F, avec des éléments en commun. L'union des deux ensembles (E U F) comprend tous les éléments de E et/ou F. L'intersection (E I F) regroupe les éléments communs à E et F. Le produit cartésien (E croix F) est une liste de couples formés d'un élément de E et d'un élément de F. Une paire est un ensemble de deux éléments. La distinction entre ensembles et listes est essentielle pour comprendre les différentes méthodes de dénombrement. Si vous avez des questions, n'hésitez pas à les poser.

Probas Terminale