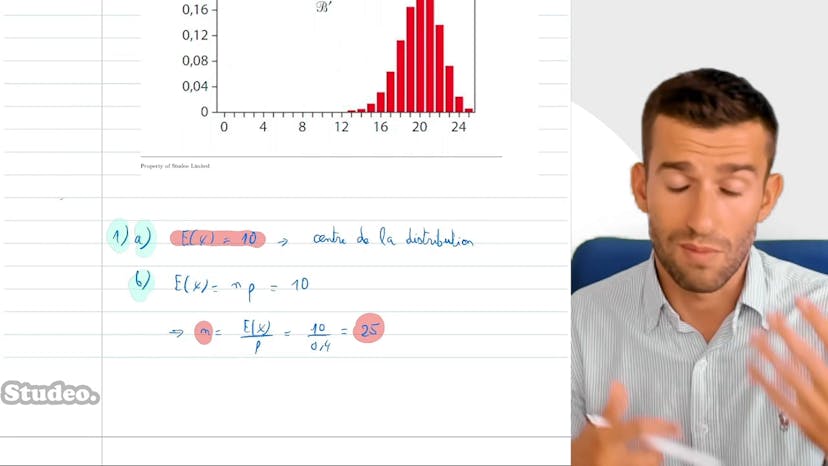
Classique : produit défectueux en usine

Ce cours traite des produits défectueux en usine. Il explique que l'usine effectue deux tests indépendants pour détecter les défauts des produits. La probabilité qu'un produit défectueux passe le premier test est de 0,12 et celle qu'il passe le deuxième test est de 0,08. Seuls les produits qui passent les deux tests sont vendus, les autres sont détruits. La première question est de savoir quelle est la probabilité qu'un produit défectueux soit mis en vente. Pour cela, on utilise les notations suivantes : V (vente) pour un produit mis en vente, T1 pour le premier test et T2 pour le deuxième test. La probabilité de vente est donc P(T1 inter T2), qui, étant donné que les tests sont indépendants, équivaut à P(T1) fois P(T2). En faisant le calcul, la probabilité est de 0,96%. Ensuite, on nous demande quelle est la probabilité qu'au moins 3 produits défectueux soient mis en vente sur 100 produits défectueux indépendants. On peut utiliser la loi binomiale avec les paramètres 100 et 0,0096, où la vente est considérée comme une réussite. La probabilité que X, la variable aléatoire représentant le nombre de ventes, soit supérieure à 3 est égale à 1 moins la probabilité que X soit strictement inférieure à 3, qui est la réunion des événements X égal à 0, X égal à 1 et X égal à 2. En faisant les calculs, on trouve que la probabilité est de 7%. Les formules utilisées sont les formules classiques de la loi binomiale : C(n, k) * P^k * (1-P)^(n-k).