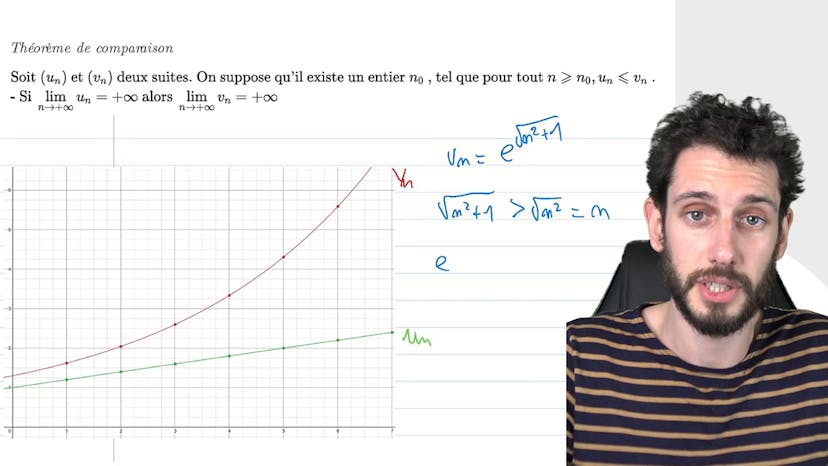
Théorème de comparaison - Illustration

Le théorème de comparaison est un outil puissant en mathématiques qui permet d'éviter de nombreuses démonstrations fastidieuses. En bref, si une suite Vn peut être comparée à une suite plus simple, et que cette dernière tend vers l'infini, alors on peut conclure que Vn tend également vers l'infini. Ce théorème est pratique car il permet de traiter des suites compliquées et de les comparer à des suites plus faciles à étudier. Par exemple, si on souhaite démontrer que la suite Vn = exp(n² + 1) tend vers l'infini, on peut la comparer à la suite Un = exp(n), qui est simple et diverge vers l'infini. En utilisant le fait que l'exponentielle est une fonction croissante, on peut conclure que Vn sera plus grand que Un, et donc tendra également vers l'infini. Ainsi, grâce au théorème de comparaison, on peut faire des économies d'efforts en évitant de faire des démonstrations détaillées. Dans la prochaine vidéo, nous verrons la démonstration de ce théorème.