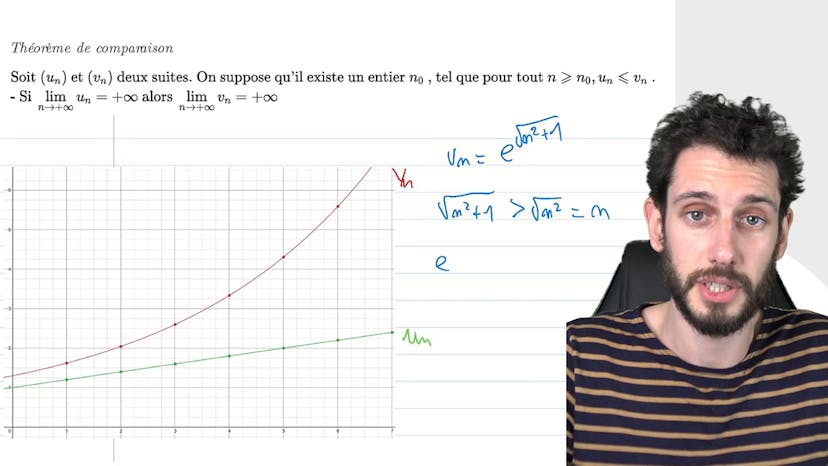
Théorème de comparaison - démonstration

Le cours explique comment démontrer le théorème de divergence en mathématiques, en utilisant une approche SEO-friendly. Le professeur commence par expliquer que malgré l'avantage de ce théorème de se passer des démonstrations en epsilon et en grand A, il est nécessaire de revenir à la définition pour la démontrer. Le professeur démontre ensuite que si la limite d'une suite tend vers l'infini, alors il existe un certain rang à partir duquel tous les éléments de cette suite sont plus grands qu'un certain nombre A positif. En utilisant cette information, le professeur conclut que pour tout A positif, il existe un certain rang à partir duquel tous les éléments de la suite sont plus grands que A. Finalement, le professeur résume cette démonstration en expliquant que pour tout A positif, il existe un certain rang à partir duquel tous les éléments de la suite sont plus grands que A, ce qui correspond à la définition de la divergence vers l'infini. En utilisant cette démonstration, il n'est plus nécessaire d'utiliser des démonstrations plus complexes avec des grands A et des petits epsilon.