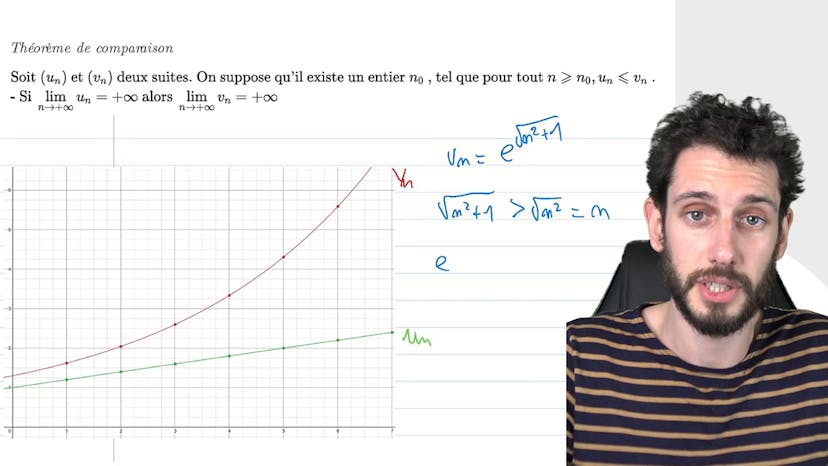
Théorème des gendarmes

Le théorème d'encadrement, également connu sous le nom de théorème des gendarmes, permet de montrer que si une suite est prise en sandwich entre deux autres suites qui convergent vers la même limite finie, alors elle converge également vers cette limite. Ce théorème peut être utilisé pour démontrer des résultats sur les suites sans avoir à s'embêter avec les définitions formelles. Dans l'exemple donné, la fonction sin(x) est tracée et semble converger vers 0. Cependant, la suite sin(n)/n est plus difficile à gérer. Pour simplifier, on peut encadrer sin(x)/x entre -1/x et 1/x. En traçant les deux fonctions, on constate qu'elles encadrent parfaitement la suite sin(n)/n. On sait que les suites 1/n et -1/n convergent vers 0, donc on peut conclure que la suite sin(n)/n converge également vers 0. Il est important de noter que même si le théorème des gendarmes peut être très pratique, il ne s'applique pas toujours et il est possible de dire moins de choses dans certaines situations. Cependant, une propriété importante à retenir est que si deux suites sont ordonnées (un toujours plus petit que vn) et qu'elles convergent, alors leurs limites respectives seront également ordonnées (la limite de vn sera plus petite que la limite de vn).