Indépendance

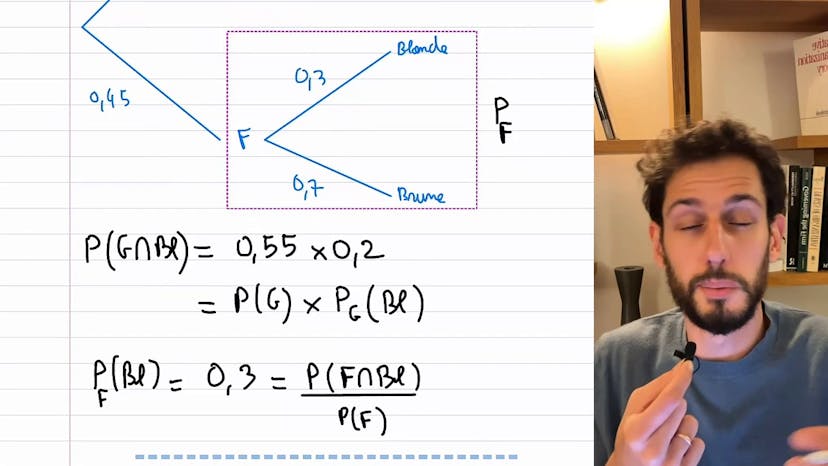
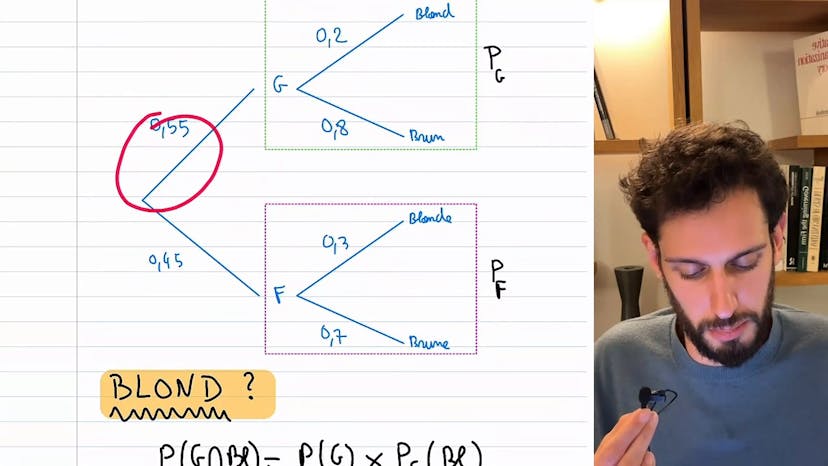
L'indépendance, une notion très importante en probabilité, peut être expliquée de manière claire en utilisant des exemples. Dans cet exemple, nous avons deux variables : le sexe (garçon ou fille) et la couleur des cheveux (blond ou brun). Nous avons également des probabilités associées à chaque événement. Par exemple, la probabilité d'être blond en étant garçon est de 0,2, et la probabilité d'être blond en étant fille est de 0,3. Pour déterminer la probabilité d'être blond dans ce lycée, nous utilisons la formule des probabilités totales. Cependant, il est important de noter que la couleur des cheveux dépend du sexe. Par conséquent, la probabilité d'être blond dépend de si vous êtes un garçon ou une fille. Ces événements sont donc dépendants. Cependant, il est également possible d'avoir des événements indépendants. Par exemple, si la probabilité d'être blond est la même pour les garçons et les filles, il s'agit d'un événement indépendant. Dans ce cas, peu importe si vous êtes un garçon ou une fille, la probabilité d'être blond est de 30%. 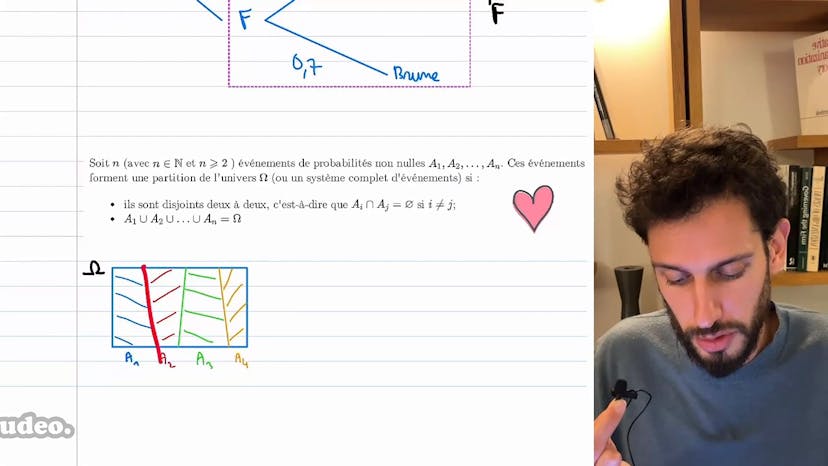Il est important de comprendre les définitions formelles en mathématiques, mais il est également utile de les considérer avec des exemples concrets. Les formalités théoriques viennent ensuite pour renforcer la compréhension. Il est également intéressant de noter que si deux événements A et B sont indépendants, leurs complémentaires (non A et non B) le sont également. En résumé, l'indépendance en probabilité se réfère à des événements qui ne dépendent pas les uns des autres. Dans le cas de l'exemple, si la probabilité d'être blond ne dépend pas du sexe, alors ces événements sont indépendants.