Application avec contexte

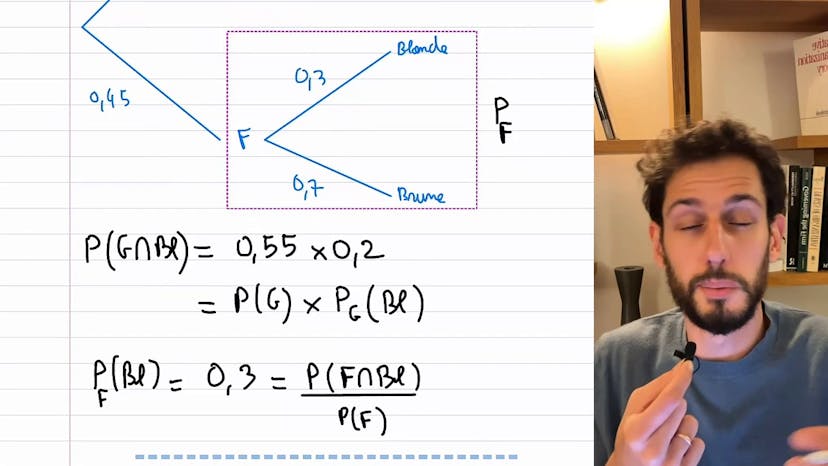
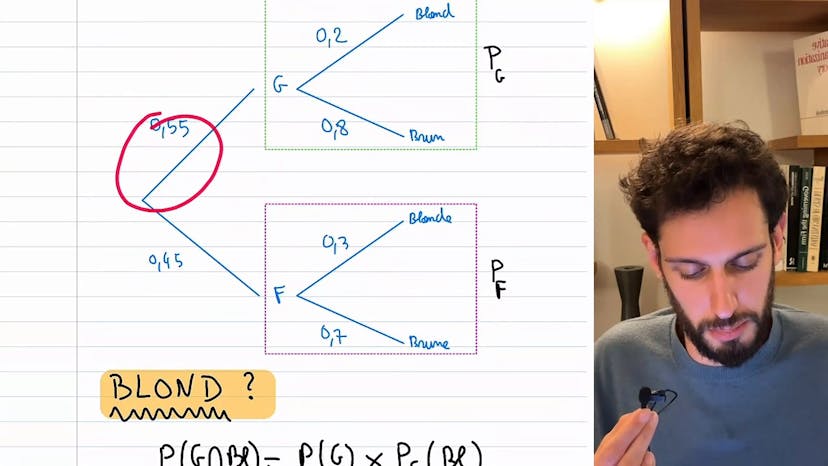
La probabilité qu'une voiture choisie aléatoirement à la sortie de l'usine soit une voiture hybride de la marque A peut être calculée en utilisant la formule des probabilités conditionnelles. Pour commencer, on sait que 60% des voitures fabriquées sont des voitures hybrides. Donc la probabilité d'avoir une voiture hybride est de 0,6, tandis que la probabilité de ne pas avoir une voiture hybride est de 0,4. Ensuite, parmi les voitures hybrides, 70% d'entre elles sont de la marque A. Donc la probabilité d'avoir une voiture hybride de la marque A est de 0,6 * 0,7 = 0,42. En utilisant ces informations, nous pouvons en conclure que la probabilité qu'une voiture choisie aléatoirement à la sortie de l'usine soit une voiture hybride de la marque A est de 0,42. 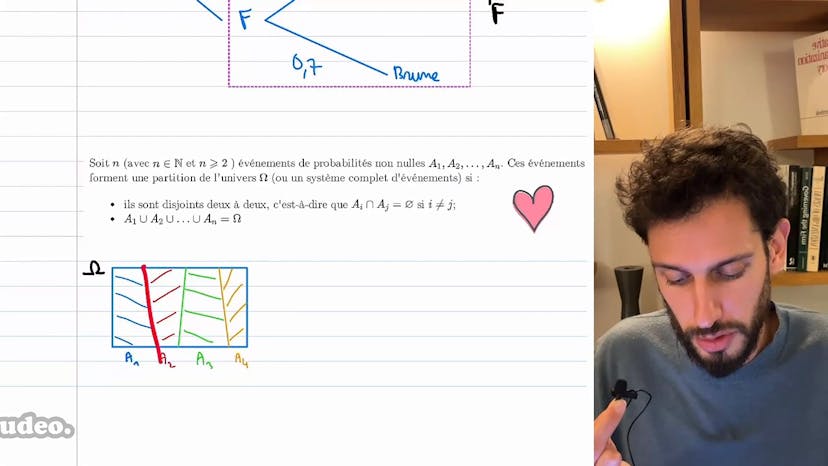Cette méthode utilise un arbre pour représenter les différents événements et permet de calculer la probabilité conditionnelle en utilisant la formule adéquate.