Arbre et urne sans remise

Dans ce cours, nous étudions une situation où nous tirons des boules d'une urne sans les remettre. Il est important de faire la distinction entre une situation avec remise (où l'on remet la boule après chaque tirage) et sans remise (où la boule tirée est retirée de l'urne). Cette distinction va influencer les probabilités tout au long du problème. Nous utilisons les notations "bi" pour représenter le fait de tirer une boule bleue au ième tirage et "ri" pour représenter le fait de tirer une boule rouge. Vu qu'il n'y a que des boules bleues et rouges dans l'urne, nous pouvons remarquer que "ri" est équivalent à "bi barre" (le complémentaire de "bi"). Par exemple, si "b1" représente le fait de tirer une boule bleue au premier tirage, alors "r1" représente le fait de ne pas tirer une boule bleue au premier tirage (c'est-à-dire tirer une boule rouge). 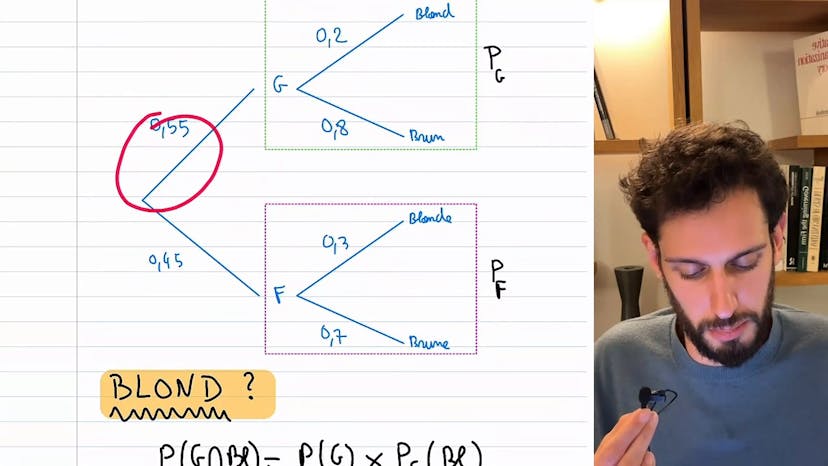L'idée ici est de représenter la situation par un arbre. Cela nous permet de visualiser plus clairement les différentes probabilités. En utilisant des dessins, nous pouvons rendre la situation plus compréhensible. Au fur et à mesure des tirages, nous modifions notre arbre pour refléter les probabilités en cours. Par exemple, si nous avons tiré une boule bleue au premier tirage, nous aurons alors une chance sur deux d'en tirer une deuxième, puis une chance sur trois d'en tirer une troisième. 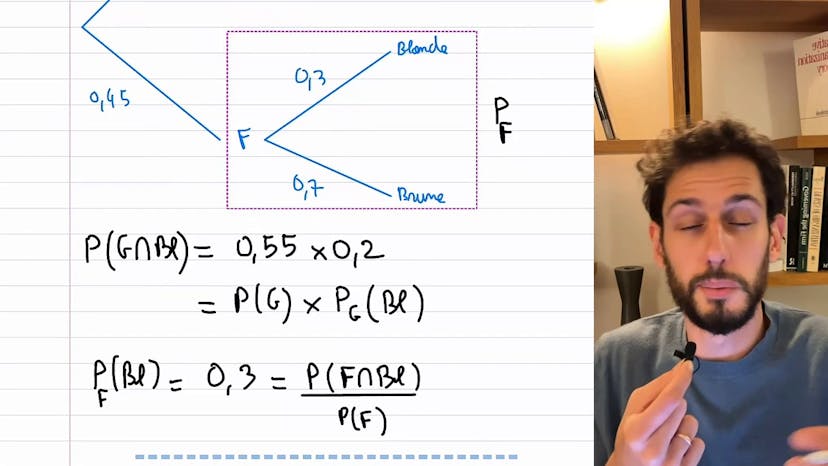Pour traduire cela en calculs, nous pouvons utiliser les probabilités conditionnelles. Par exemple, pour calculer la probabilité d'avoir tiré deux boules rouges, nous pouvons écrire "proba de R1 inter R2". Cette expression équivaut à la probabilité d'avoir tiré une boule rouge au premier tirage, puis dans cet univers, la probabilité d'avoir tiré une boule rouge au deuxième tirage. En résolvant ces calculs, nous obtenons les probabilités recherchées. Dans cet exemple, la probabilité d'avoir tiré deux boules rouges est de 1/6. Il est important de bien comprendre les énoncés et de faire attention à la présence ou non de remise dans le problème. N'hésitez pas à poser des questions si quelque chose n'est pas clair et je vous retrouve dans une prochaine vidéo.