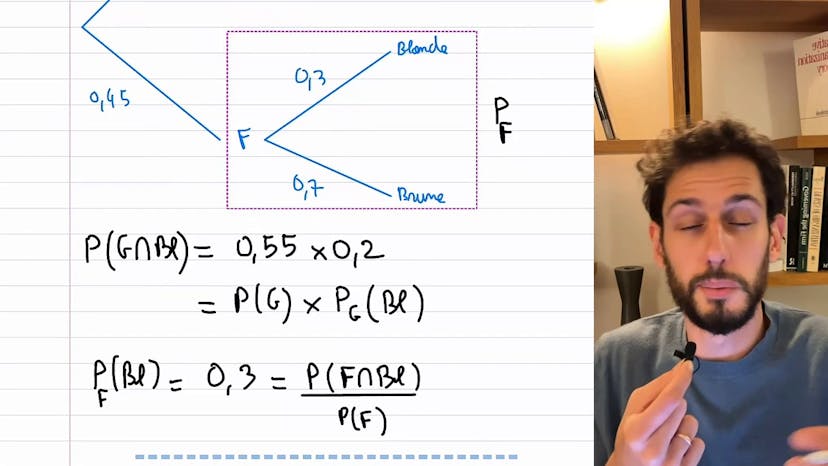
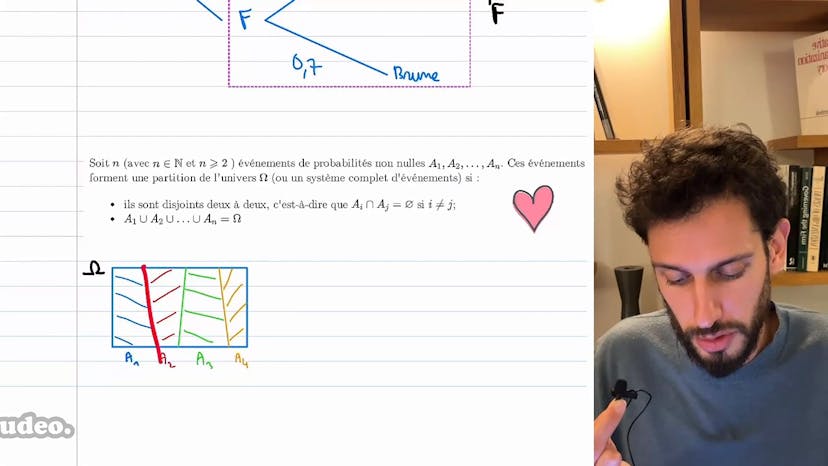
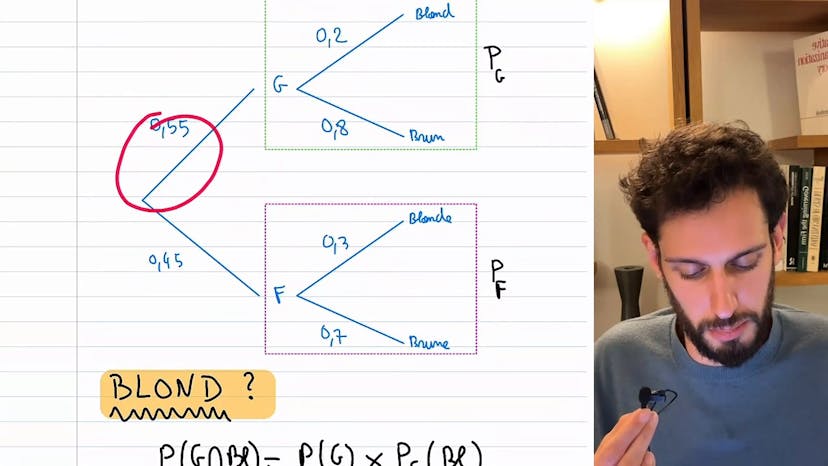
Probabilité de l’intersection

Dans cet exercice, nous voulons illustrer une inégalité concernant la probabilité de l'intersection de deux événements. Plus précisément, nous voulons montrer que cette probabilité est comprise entre deux valeurs. Pour commencer, nous allons examiner la partie de droite de l'inégalité. La probabilité de l'intersection est égale à la plus petite valeur entre 0 et la somme des probabilités des deux événements moins 1, ainsi que le minimum des probabilités individuelles. Pour le démontrer, nous utilisons la formule appropriée. Une autre méthode aurait pu être utilisée, mais j'ai préféré utiliser cette approche. Nous utilisons la formule et constatons que l'événement A est inclus dans l'union, tout comme B. Par conséquent, la probabilité de l'union est plus grande que celle de A et aussi que celle de B. En conséquence, P(A∩B) est négatif par rapport à P(A) et P(B). De même, P(B∩A) est également négatif par rapport à P(B) et P(A∪B). En remplaçant ces valeurs dans l'inégalité, nous constatons que P(A∩B) est plus petit à la fois que P(A) et que P(B), ce qui signifie qu'il est plus petit que le minimum des deux probabilités. Ensuite, nous montrons l'égalité dans l'autre sens. Tout d'abord, nous devons démontrer que la probabilité de l'intersection est plus grande que le maximum des deux probabilités. Cela signifie que nous devons montrer qu'elle est plus grande que l'une et plus grande que l'autre. Nous savons que cela est supérieur à zéro car il s'agit d'une probabilité. Il nous reste à prouver qu'elle est plus grande que la valeur maximale. Comme je l'ai mentionné précédemment, P(A∪B) est plus petit que 1, donc P(A∩B), qui est égal à P(A) + P(B) - P(A∪B), est plus grand que P(A)+P(B)-1. Par conséquent, il est plus grand que zéro et que cette valeur maximale, ce qui conclut notre exercice.