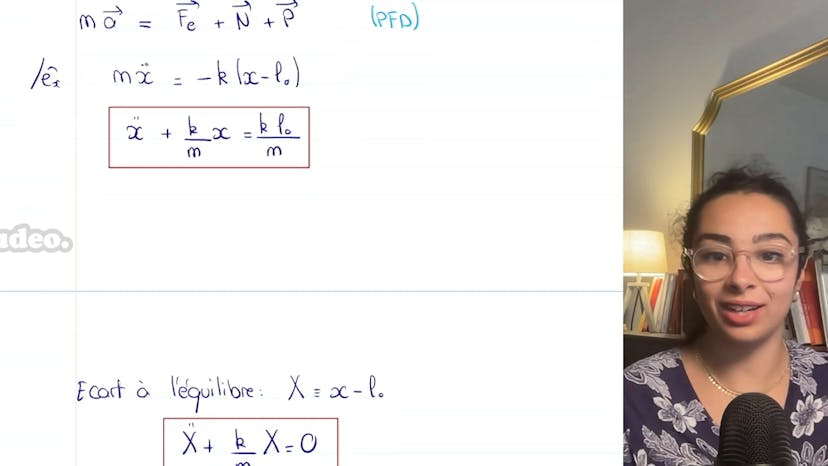Tous les sujets
Tous les sujets Maths
Maths Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée Prépa Examens
Prépa Examens
 Tous les sujets
Tous les sujets Maths
Maths Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée Prépa Examens
Prépa Examens
Système à deux ressort
Dans ce cours, nous étudions un système composé de deux ressorts identiques placés côte à côte. Nous commençons par appliquer le principe fondamental de la dynamique pour trouver les forces exercées par les ressorts sur la masse. En dessinant les schémas représentant les ressorts comprimés ou étirés, nous pouvons déterminer les directions et les signes des forces. En appliquant le principe fondamental de la dynamique, nous obtenons une équation de mouvement où la masse est soumise à une force élastique de la forme KL - 2X, où K est la constante du ressort, L est la longueur du ressort à vide et X est la position de la masse par rapport à l'équilibre.
Ensuite, nous étudions le cas des oscillations amorties en ajoutant une force de frottement à l'équation de mouvement. Cette force est de la forme -βX', où β est le coefficient de frottement et X' est la vitesse de la masse. Nous obtenons ainsi une équation d'oscillateur amorti X'' + βX' + 2K/MX = 0. Nous rappelons les différentes formes de cette équation et discutons des régimes d'oscillation en fonction de la valeur de β.
Enfin, nous traitons du retour rapide à la position d'équilibre. Nous trouvons que le régime critique pour un retour rapide correspond à β = 2√(2K/M), où la masse oscille avec une décrépitude minimale. Nous calculons également la période et le temps caractéristique de retour à l'équilibre dans ce régime.