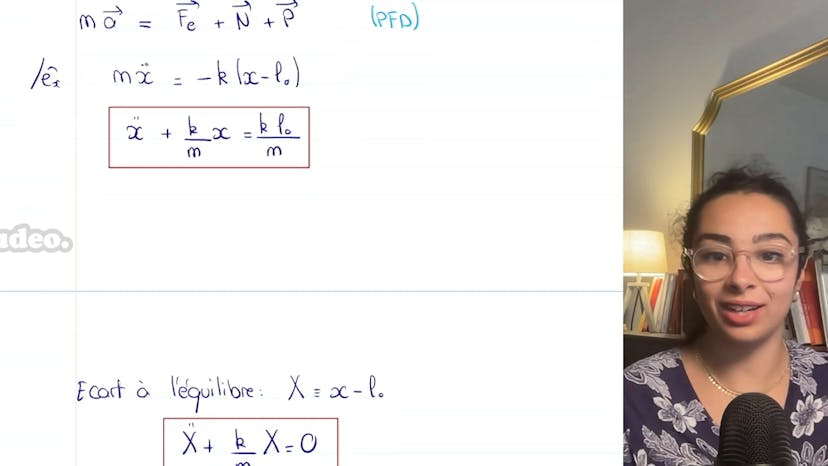Mesure du champ de pesanteur

Bonjour à tous, aujourd'hui nous allons aborder la mesure du champ de pesanteur à l'aide d'un pendule simple. Pour commencer, nous allons démontrer que la période du pendule est égale à 2 pi racine de L sur G, où L représente la longueur du pendule et G le champ de pesanteur. Pour cela, nous partirons de l'équation du pendule simple θ seconde plus G sur L sine θ est égale à 0. Dans la limite des petits angles, nous pouvons approximer sine θ par θ. Ainsi, nous obtenons une équation d'oscillateur harmonique avec oméga 0 carré égal à G sur L. En utilisant la formule de la période T0 égale à deux pi sur oméga 0, nous arrivons à T0 égale à deux pi racine de L sur G. Il est important de noter que la valeur de G peut varier d'un point à un autre sur Terre en raison de l'altitude et de la rotation de la Terre. Ainsi, en 1672, un astronome se rend à Cayenne avec une horloge à pendule réglée à Paris. Il constate que son horloge retarde de 2 minutes et 28 secondes par jour. Nous devons donc déterminer la valeur du champ de pesanteur à Cayenne. En utilisant les périodes des pendules à Paris (T0) et à Cayenne (T1), nous allons chercher à combiner ces informations pour faire apparaître un rapport intéressant. En calculant Tp sur Tc, nous obtenons racine de G1 sur G0. Donc G1 est égal à G0 fois T0 sur T1, le tout au carré. En connaissant T1 et l'écart de temps (delta T) entre les deux pendules, nous pouvons déterminer G1. Ainsi, G1 équivaut à G0 fois T0 sur T0 plus delta T au carré, soit une valeur de 9,78 mètres par seconde au carré. J'espère que cet exercice vous a été utile. À bientôt pour de nouveaux exercices sur la mesure du champ de pesanteur.