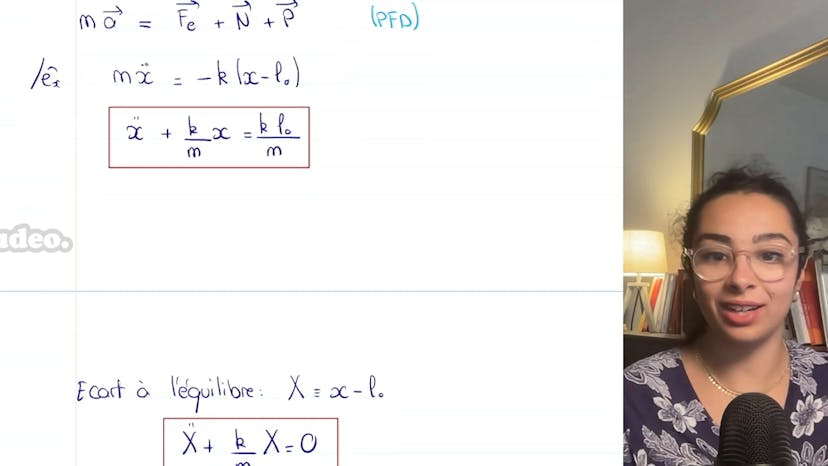Bille suspendue à un fil

Dans cet exercice, nous étudions un pendule simple constitué d'une bille suspendue à un fil inextensible de longueur L égale à 1 m. La bille est écartée de sa position initiale de 60° et est ensuite lâchée sans vitesse initiale. Nous devons déterminer la vitesse en fonction de θ (l'angle de déviation) et trouver l'angle pour lequel la vitesse est maximale. Pour résoudre ce problème, nous commençons par établir un bilan des forces. Nous identifions le poids P qui est égal à mg, ainsi que la tension du fil -TER. En ce qui concerne l'aspect cinématique, nous avons l'équation OM = LER, où L est une constante. Par projection de cette équation, nous obtenons les équations MLθ.² = T + mg cosθ et MLθ² = -mg sinθ, où T est la tension du fil. Afin d'éliminer le temps et obtenir une équation reliant la vitesse et θ, nous multiplions la deuxième équation par θ point (la dérivée de θ par rapport au temps). En intégrant cette équation par rapport à dθ entre les instants initial et T, nous obtenons L/2θ point²(T) = g cosθ - g cosθ0. Après avoir traduit cette équation en fonction de θ, nous obtenons l'expression de la vitesse en fonction de θ : v = racine de 2g cosθ - cosθ0. La vitesse est maximale lorsque cosθ = 1, ce qui correspond à θ = 0. En ce qui concerne l'accélération radiale, nous utilisons l'équation Lθ point² - v²/L. En utilisant l'expression précédente pour la vitesse, nous trouvons que l'accélération radiale est égale à -2g cosθ + 2g cosθ0. Pour l'expression de la tension du fil, nous utilisons l'équation MLθ.² = mg cosθ - T. En utilisant l'expression de la vitesse que nous avons obtenu précédemment, nous trouvons que la tension du fil est T = mg(3 cosθ - 2 cosθ0). Nous remarquons également que la tension est maximale lorsque cosθ = 1, donc lorsque θ = 0. En conclusion, cet exercice sur le pendule simple nous permet de comprendre comment une bille suspendue à un fil inextensible se comporte en termes de vitesse, accélération et tension du fil en fonction de l'angle de déviation θ. Ces concepts peuvent également être appliqués à d'autres types de problèmes, tels que les problèmes de décollement.