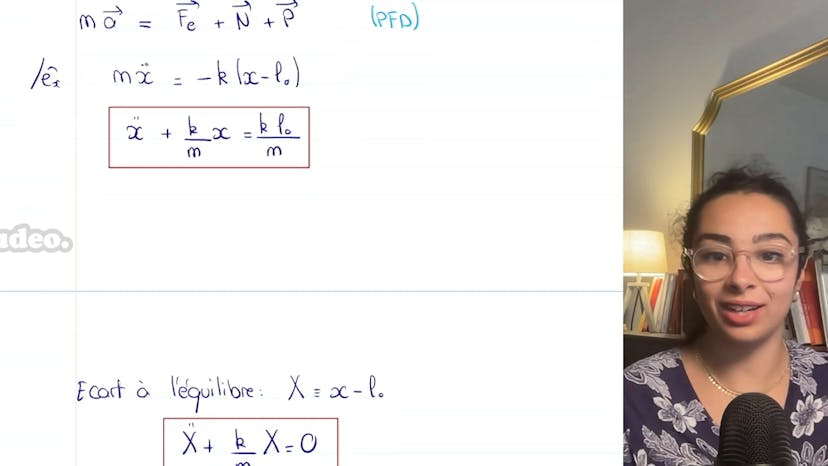Mouvement circulaire et ressort

Dans ce cours, nous abordons le mouvement circulaire avec un ressort. Une masse (m) est placée sur un plan horizontal et reliée à un point fixe (o) par un ressort de constante de raideur (k) et de longueur initiale (l0). Au départ, la masse est lancée avec une vitesse initiale (v0). Pour déterminer le rayon du cercle et la direction de v0, nous devons tenir compte du fait que le ressort ne doit ni être étiré ni comprimé. Donc, le rayon du cercle est égal à la longueur initiale du ressort (L0). Quant à la direction de v0, elle doit être tangente au cercle, c'est-à-dire selon la direction Eθ. Ensuite, nous montrons que si le mouvement est circulaire, alors il est également uniforme. En effectuant un bilan des forces, nous trouvons la force de rappel du ressort, le poids et la réaction du support. En utilisant les équations de la cinématique, nous trouvons l'expression de l'accélération. Nous pouvons réarranger cette expression pour obtenir une forme pratique : DV/DT Eθ - V^2/LER. Cette forme nous permet de voir que si le mouvement est uniforme, alors DV/DT est nul. Si nous projetons la force sur ER, nous obtenons une équation établissant que la vitesse est constante. Finalement, nous donnons une condition sur L pour que le mouvement soit circulaire. Nous constatons que cette condition est cohérente avec notre constatation précédente sur le mouvement uniforme. La vitesse initiale (v0) peut être calculée en utilisant l'expression v0 = K(L-L0)L/M. Ce cours combine les concepts des oscillateurs et des forces centrales, car il s'agit d'un oscillateur harmonique en rotation. Il n'y a pas de difficultés majeures, mais il est recommandé de retenir la forme pratique de l'expression lorsque nous traitons des forces centrales.