Intuition et déf

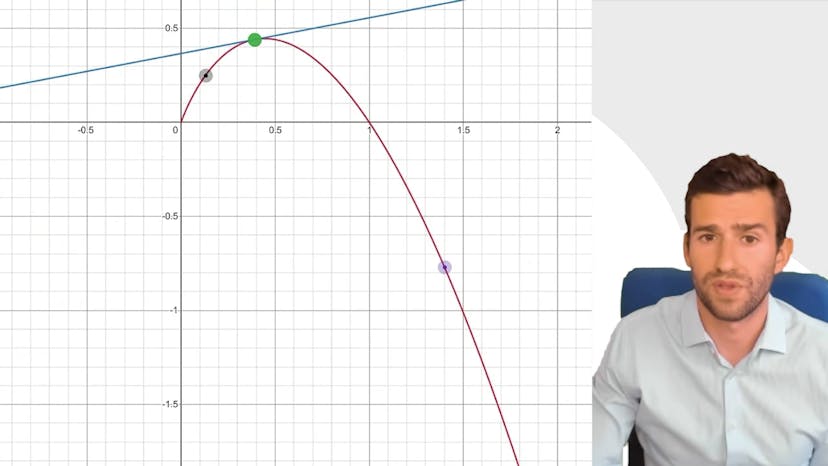
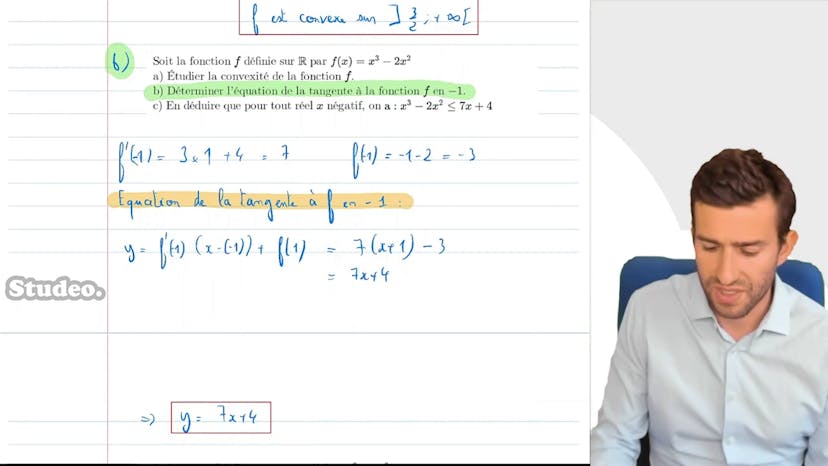
La vidéo traite de la convexité et commence par expliquer que l'on peut comprendre très simplement ce qu'est une fonction convexe ou concave avec l'aide d'un graphique. L'explication visuelle consiste à dire que convex c'est quand ça monte comme ça, et concave c'est quand ça monte mais pas trop vite. La vidéo introduit ensuite la définition mathématique officielle de la convexité, qui consiste à définir une séquente comme toute droite qui relie deux points d'une courbe, et une fonction convexe si, pour tout réel X de l'intervalle I, la courbe est en dessous de cette séquente. La vidéo explique que cette définition s'applique à toutes les fonctions, qu'elles soient continues ou pas. Enfin, la vidéo présente deux exemples de fonctions convexes et concaves, avec des graphiques pour illustrer ces concepts.