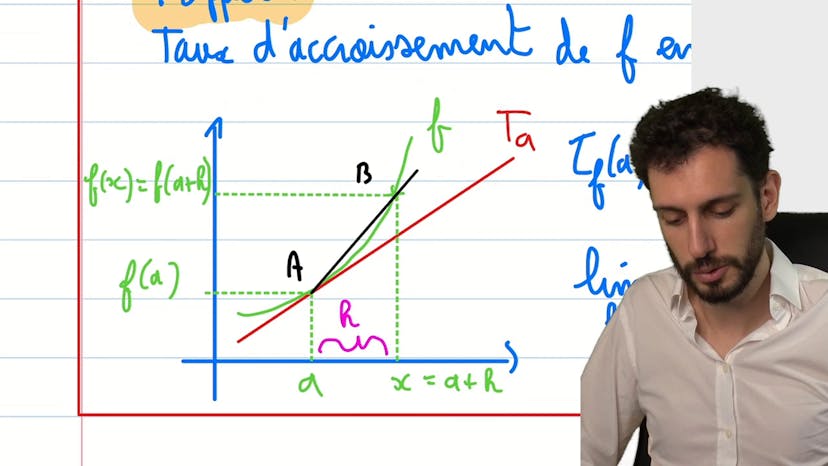
Nombre dérivé : la quantité conjuguée

Dans cet exercice de mathématiques, nous apprenons comment calculer la limite d'un taux d'accroissement pour montrer qu'une fonction est dérivable en un point. Pour cela, nous utilisons la méthode de quantité conjuguée qui est une transformation classique lorsque nous avons une expression de racine. Nous examinons également le problème de la division de 0 par 0, où il n'y a pas de règle spécifique à suivre. Nous cherchons ensuite une identité remarquable qui nous permet de simplifier le problème et de trouver la limite du taux d'accroissement. Cette méthode de quantité conjuguée est importante et peut être utilisée dans de nombreux autres exercices. À la fin, nous trouvons que la limite est égale à un sixième.