Tous les sujets
Maths- Nombres et calculs
- Géométrie
- Fonctions
- Stats et Probas
- Analyse
- Géométrie
- Probas et Stats
- Analyse (spé)
- Suites
- Limites des Fonctions
- Continuité et Dérivabilité
- Dérivation
- Convexité
- Logarithme
- Fonctions Trigonométriques
- Primitives & Équations Différentielles
- Calcul Intégral
- Géométrie (spé)
- Probabilités (spé)
- Arithmétique (exp)
- Complexes (exp)
- Analyse
- Algèbre
- Analyse
- Algèbre
- Probabilités
SecondePremièreTerminale2BAC SM MarocMPSI/PCSI
Physique-Chimie
Corrigés de BAC- Prépa Examens
- Révisions Maths lycée
- Tous les sujets
- Maths
- Nombres et calculs
- Géométrie
- Fonctions
- Stats et Probas
- Analyse
- Géométrie
- Probas et Stats
- Analyse (spé)
- Suites
- Limites des Fonctions
- Continuité et Dérivabilité
- Dérivation
- Convexité
- Logarithme
- Fonctions Trigonométriques
- Primitives & Équations Différentielles
- Calcul Intégral
- Géométrie (spé)
- Probabilités (spé)
- Arithmétique (exp)
- Complexes (exp)
- Analyse
- Algèbre
- Analyse
- Algèbre
- Probabilités
SecondePremièreTerminale2BAC SM MarocMPSI/PCSI - Physique-Chimie
- Corrigés de BAC
- Prépa Examens
- Révisions Maths lycée
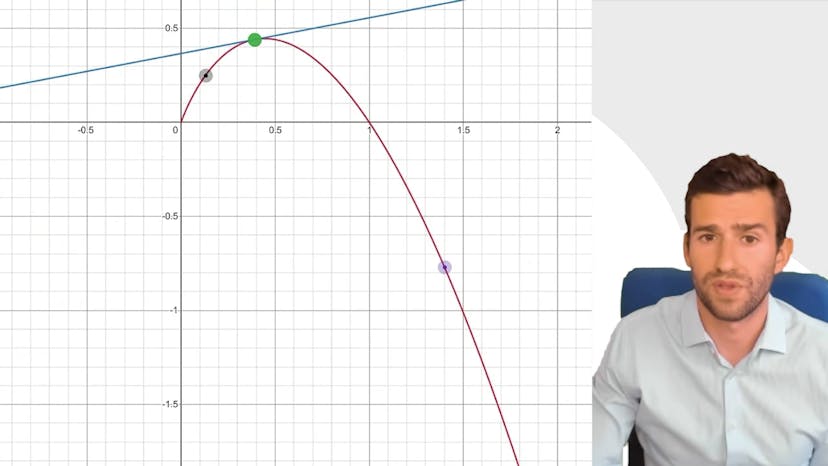
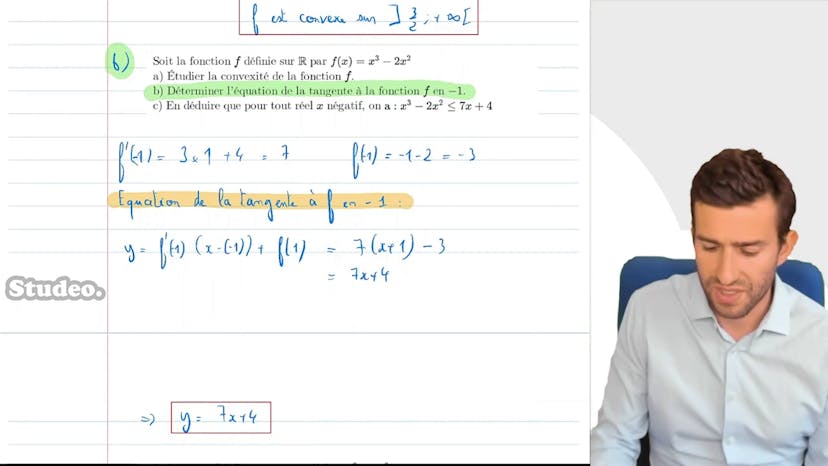
Fonctions cubes et convexité
Le cours aborde différents paramètres (A, B, C, D) et propose une démonstration générale sur les fonctions x³. Il met en évidence l'intuition graphique selon laquelle une fonction x³ avec un coefficient positif est concave, tandis qu'une fonction avec un coefficient négatif est convexe. Pour étudier la convexité de la fonction f, il faut analyser le signe de f prime prime, qui dépend de la valeur de A. Si A est positif, la fonction est concave, alors que si A est négatif, elle est convexe. Une erreur courante est de ne pas distinguer les différents cas. L'exercice demande également d'appliquer ce résultat à un exemple spécifique.
