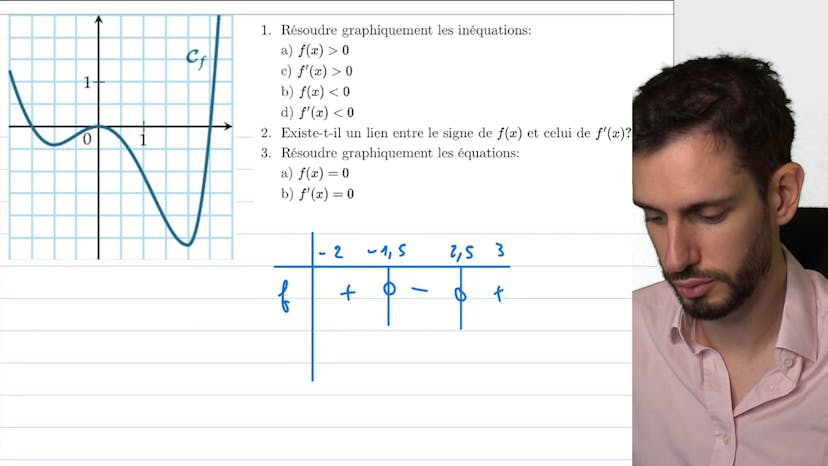
Qui est f qui est f' sur un graphique ?

Ce cours explique la relation entre une fonction et sa dérivée. Lorsqu'une fonction est dérivable, elle est croissante si sa dérivée est positive et décroissante si sa dérivée est négative. Pour analyser deux graphes et déterminer lequel représente la dérivée, il suffit d'observer le signe de chaque fonction. Si la première fonction est positive jusqu'à (-0,5) et croit jusqu'à (-0,5), et que la seconde fonction est négative jusqu'à 0 et décroît jusqu'à 0, alors la première fonction est la dérivée. En revanche, si la première fonction est négative jusqu'à (-0,6) mais la seconde fonction décroît jusqu'à (-0,1), cela ne correspond pas à une dérivée. De plus, si la première fonction est positive de (-0,6) à 0, il faudrait qu'elle croisse entre les deux, ce qui n'est pas le cas. Finalement, si la première fonction devait décroître uniquement à partir de 0,7, cela ne correspondrait pas non plus. En conclusion, pour une fonction dérivable, on peut déterminer si elle croît ou décroît en observant le signe de sa dérivée.