Lien entre signe de f et de f' ?

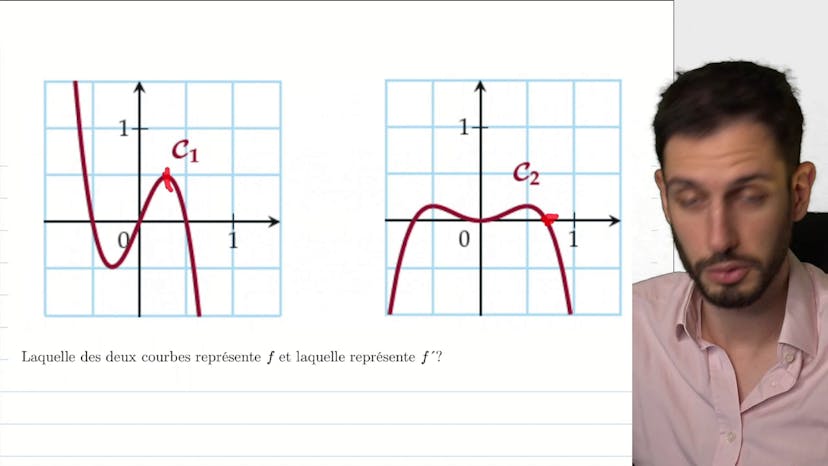
Ce cours aborde la résolution graphique des inéquations et met en évidence le lien entre la positivité de la fonction f(2x) et la croissance de sa dérivée f'(2x). Nous examinons les différentes régions où f(2x) est positif et négatif, ainsi que le signe de f'(2x) dans ces régions. Nous constatons qu'il n'y a pas de lien direct entre le signe de f(2x) et celui de f'(2x). Ensuite, nous résolvons graphiquement les équations f(2x) = 0 et f'(2x) = 0 en identifiant les points où la courbe touche l'axe des x et les points où la tangente à la courbe a une pente nulle. L'idée principale de cet exercice est de ne pas confondre les notions de positivité de la fonction et de sa dérivée, et de comprendre que différents scénarios sont possibles en termes de croissance de la fonction et du signe de sa dérivée.