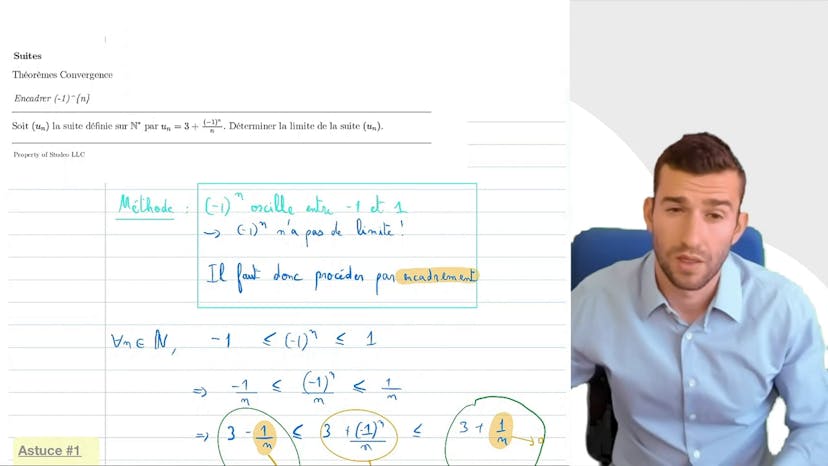Suite majorée, minorée & Th de convergence monotone

Dans ce cours, le professeur explique les concepts de majoration, de minoration et de bornage des suites. Une suite est dite majorée lorsqu'elle est bloquée par une certaine valeur et ne peut pas dépasser cette valeur. Il peut y avoir plusieurs majorants pour une suite. De même, une suite est dite minorée lorsqu'elle ne peut pas descendre en dessous d'une certaine valeur. Une suite est dite bornée lorsque elle est à la fois majorée et minorée. Le professeur illustre ces notions à l'aide de quelques exemples de suites bornées. Il mentionne le théorème de convergence monotone, qui associe le fait d'être croissante à celui d'être majorée. Ce théorème permet de conclure que si une suite est croissante et majorée, alors elle converge. Cependant, il précise que ce théorème ne donne pas la valeur de la limite de la suite. Le professeur présente également la version du théorème de convergence monotone pour les suites décroissantes et minorées, ainsi que pour les suites croissantes et non majorées, et les suites décroissantes et non minorées. Il insiste sur le fait que la réciproque du théorème de convergence monotone est fausse, c'est-à-dire que converger ne signifie pas forcément être croissante majorée ou décroissante minorée. Il donne des contre-exemples pour illustrer ce point, notamment la suite sinus sur n qui converge vers 0 mais oscille de manière "moche". Enfin, il conclut en soulignant l'importance de ne pas se laisser piéger par des fausses idées sur les suites qui convergent. N'hésitez pas à consulter la FAQ ou à discuter avec les autres étudiants si vous avez des questions.