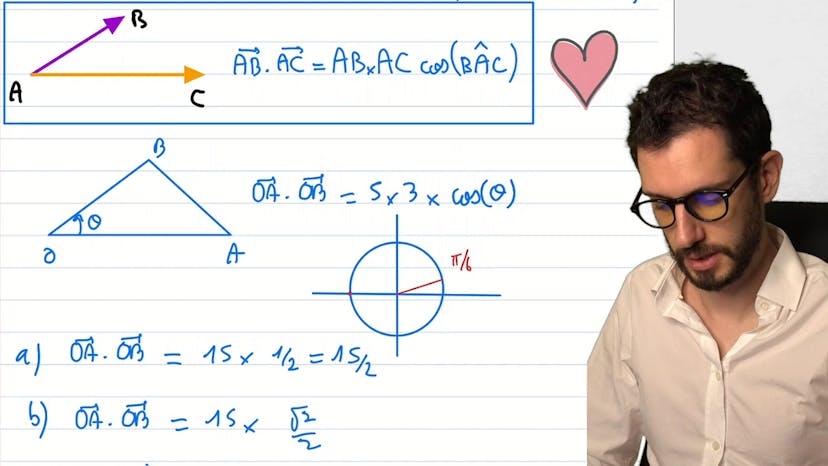Tous les sujets
Maths- Nombres et calculs
- Géométrie
- Fonctions
- Stats et Probas
- Analyse
- Géométrie
- Produit Scalaire
- Géométrie avec Repères
- Probas et Stats
- Analyse (spé)
- Géométrie (spé)
- Probabilités (spé)
- Arithmétique (exp)
- Complexes (exp)
- Analyse
- Algèbre
- Analyse
- Algèbre
- Probabilités
SecondePremièreTerminale2BAC SM MarocMPSI/PCSI
Physique-Chimie
Corrigés de BAC- Prépa Examens
- Révisions Maths lycée
- Tous les sujets
- Maths
- Nombres et calculs
- Géométrie
- Fonctions
- Stats et Probas
- Analyse
- Géométrie
- Produit Scalaire
- Géométrie avec Repères
- Probas et Stats
- Analyse (spé)
- Géométrie (spé)
- Probabilités (spé)
- Arithmétique (exp)
- Complexes (exp)
- Analyse
- Algèbre
- Analyse
- Algèbre
- Probabilités
SecondePremièreTerminale2BAC SM MarocMPSI/PCSI - Physique-Chimie
- Corrigés de BAC
- Prépa Examens
- Révisions Maths lycée
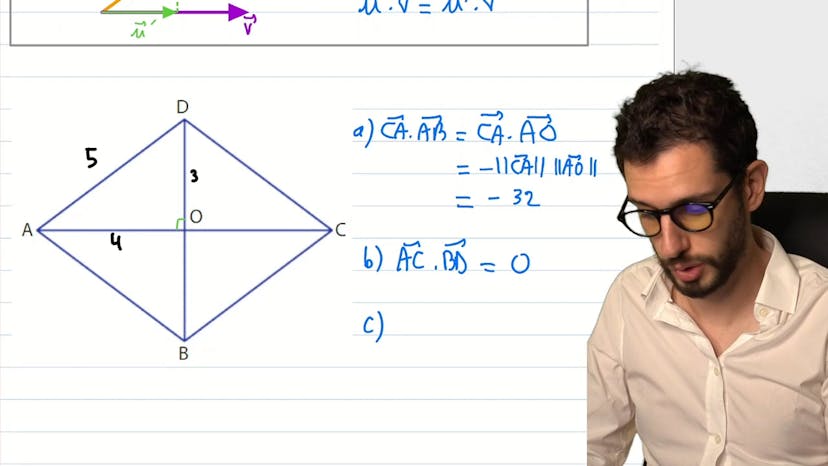
Produit scalaire : 0 calculs, que des projections
Dans cet exercice, on observe un triangle OAB et on cherche à démontrer que OA' x OB est égal à OA x OB'. On commence par trouver les points A' et B', qui sont les projections orthogonales de A et B sur les côtés opposés. Ensuite, on utilise la propriété du produit scalaire pour exprimer OA' x OB en fonction d'un produit scalaire, et on remarque que ce produit scalaire est également égal à OA' x OB'. Ce faisant, on peut exprimer OA' x OB' en fonction d'un produit scalaire, ce qui nous permet de prouver que OA' x OB est bien égal à OA x OB'. Cet exercice montre l'utilité du produit scalaire dans la résolution de problèmes de géométrie.
