Cours de Probabilités en Ligne par les Meilleurs Professeurs - Probabilités

Cours par cas pratiques !

Dans cette transcription de cours, nous abordons le dénombrement des anagrammes, c'est-à-dire le nombre de façons de combiner les lettres d'un mot donné. Nous commençons par l'exemple du mot "ABC" et expliquons que le nombre d'anagrammes est égal à 3 factorielle, car il y a 3 lettres que nous pouvons placer dans 3 cases. Ensuite, nous abordons des mots avec des lettres répétées, comme "CHA", "CHIEN" et "VALISE". Nous expliquons que le raisonnement est le même, mais nous devons tenir compte des permutations possibles pour les lettres identiques. Par exemple, dans le mot "AXA", il y a 3 anagrammes possibles, mais nous devons diviser par 2 car les deux "A" sont identiques. Pour des mots plus complexes comme "ABRACADABRA", nous devons prendre en compte les permutations pour chaque lettre répétée. Par exemple, il y a 5 "A" et 2 "B" dans ce mot, donc nous devons diviser par 5 factorielle pour les "A" et par 2 factorielle pour les "B". En utilisant cette méthode de raisonnement et de correction, nous pouvons déterminer le nombre d'anagrammes pour n'importe quel mot donné. Cela implique de compter le nombre total de lettres, de tenir compte des lettres répétées et de diviser par les permutations possibles pour chaque lettre répétée. Ce processus peut sembler compliqué, mais il permet d'obtenir le résultat correct.

Déterminer des ensembles

Dans ce cours, on apprend la première méthode de dénombrement. On distingue deux concepts importants : les ensembles et les listes. Un ensemble est comme un sac qui contient différentes choses, sans ordre particulier. Une liste, quant à elle, est une collection d'éléments organisés selon un ordre spécifique. Il faut faire attention à ne pas confondre les deux. Dans les ensembles, l'ordre des éléments ne compte pas. Par exemple, le sac contenant AB est équivalent au sac contenant BA. En revanche, dans les listes, chaque élément a un numéro d'ordre spécifique (par exemple, les coordonnées 1-2 ne sont pas les mêmes que les coordonnées 2-1). Lorsqu'on travaille avec des ensembles, on utilise des opérations combinatoires, qui seront abordées dans les prochaines méthodes. Par exemple, on peut prendre l'union (notée U) de deux ensembles, ce qui donne un nouvel ensemble contenant tous les éléments des deux ensembles (sans les répéter). On peut également prendre l'intersection (notée ∩), qui donne les éléments communs aux deux ensembles. On introduit également le concept de produit cartésien, qui consiste à former des couples d'éléments provenant de deux ensembles différents. Par exemple, si on prend le produit cartésien de deux ensembles E et F, on obtient un ensemble de couples, où le premier élément du couple provient de E et le deuxième élément provient de F. Ensuite, on explore les paires, qui sont des ensembles de deux éléments. On peut former toutes les paires possibles à partir d'un ensemble donné. Il faut cependant faire attention à ne pas compter deux fois les paires qui contiennent les mêmes éléments (par exemple, la paire HE est la même que EH). En résumé, il est important de distinguer entre ensembles et listes, car cela influence le dénombrement des possibilités. Les opérations sur les ensembles (union, intersection) et le produit cartésien permettent de combiner et de comparer des ensembles. Les paires peuvent être formées à partir d'un ensemble donné en prenant toutes les combinaisons de deux éléments.

Utiliser un diagramme

Les diagrammes sont très utiles pour représenter visuellement des informations et faciliter leur compréhension. Dans cet exemple, nous utilisons un diagramme pour dénombrer des éléments appartenant ou non à une sous-catégorie. Prenons l'exemple d'une station de sport d'hiver avec 20 touristes. Parmi ces touristes, 14 pratiquent le ski de piste, 7 pratiquent le ski de fond et 4 pratiquent les deux. Sur le diagramme, les 20 touristes sont représentés par une bulle bleue. À l'intérieur de cette bulle, nous avons 10 touristes qui pratiquent le ski de piste, 4 touristes qui pratiquent à la fois le ski de piste et le ski de fond, et 3 touristes qui pratiquent uniquement le ski de fond. En additionnant ces chiffres, nous obtenons bien les 14 touristes qui pratiquent le ski de piste et les 7 touristes qui pratiquent le ski de fond. Maintenant, il reste à déduire combien de touristes ne pratiquent aucune de ces activités. En comptant les touristes pratiquant le ski de piste, le ski de fond et les deux activités, soit 10 + 4 + 3, nous obtenons 17. Étant donné qu'il y avait initialement 20 touristes, cela signifie qu'il y a 3 touristes qui ne pratiquent aucune activité. Ce petit exemple illustre la méthode de représentation par diagrammes, qui peut être utilisée même dans des cas plus complexes. Les bulles permettent de visualiser facilement les différents éléments et de mieux s'y retrouver. C'est ainsi que fonctionnent les diagrammes.

Dénombrer des ensembles simples

Dans ce cours, nous allons apprendre à dénombrer des résultats en utilisant des exemples concrets. Premièrement, nous lançons une pièce pile ou face 7 fois de suite. Nous voulons déterminer le nombre de résultats possibles. Nous devons nous poser deux questions. Tout d'abord, est-ce une liste ou un ensemble et est-ce que l'ordre compte ? Dans ce cas, l'ordre compte et nous pouvons répéter les résultats. Donc le nombre de tirages possibles est de 2 puissance 7. Deuxièmement, nous avons deux joueurs qui jouent au domino et qui reçoivent 7 dominos chacun parmi les 28 dominos du jeu. Nous devons déterminer le nombre de distributions possibles. Dans ce cas, nous considérons que c'est une liste et que l'ordre compte. Il n'y a pas de répétition. Donc le nombre de distributions possibles est égal à 28 factorial sur 14 factorial. Enfin, nous disposons de 4 gâteaux pour 4 invités. Nous devons déterminer le nombre de choix possibles. Chaque invité aura un gâteau et il n'y a pas de répétition possible. L'ordre compte. Donc le nombre de choix possibles est égal à 4 factorial. Pour résumer, lorsque nous dénombrons, nous devons nous poser deux questions : est-ce que l'ordre compte et est-ce que nous pouvons répéter les résultats ? Si vous avez des questions supplémentaires, n'hésitez pas à consulter la FAQ.

Tirage successif sans remise

L'énoncé du cours concerne le tirage successif sans remise d'un certain nombre d'élèves se tenant en rang. Il s'agit de déterminer combien de façons il est possible de les ranger. Il est important de préciser si l'on considère une liste ordonnée ou un ensemble, ainsi que la présence ou non de répétition. Dans cet exemple particulier, l'ordre compte et il n'y a pas de répétition possible. Pour trouver le nombre de façons de ranger les élèves, on utilise la formule générale de P tirages successifs sans remise dans un ensemble à N éléments. Ainsi, si on a N élèves et que l'on en range P, le nombre de possibilités est donné par la formule N! / (N-P)!. Pour mémoriser cette formule, il est utile de retenir N! / (N-P!) pour les tirages successifs sans remise. C'est ainsi que l'on procède pour le tirage successif sans remise.

Tirage successif avec remise

L'exercice consiste à compter le nombre de poignées de mains échangées entre deux équipes de 15 personnes chacune. Pour résoudre ce problème, il est nécessaire d'analyser la nature de la poignée de main. Une poignée de main représente une paire de personnes, une personne de chaque équipe. Ainsi, pour déterminer le nombre de paires possibles, il faut multiplier le nombre de personnes dans chaque équipe. Dans ce cas, il y a 15 possibilités dans l'équipe 1 et 12 possibilités dans l'équipe 2, soit un total de 180 poignées de mains échangées. Il est important de noter que chaque poignée de main est comptée une seule fois, car elles sont répertoriées dans des listes distinctes, en accordant une importance à l'ordre des équipes. Ainsi, le résultat obtenu est sûr et ne compte pas deux fois les mêmes personnes ou poignées de mains. En comprenant clairement ce qui est réellement compté, c'est-à-dire des paires, le problème devient beaucoup plus simple à résoudre.

Principe multiplicatif et arbre pondéré

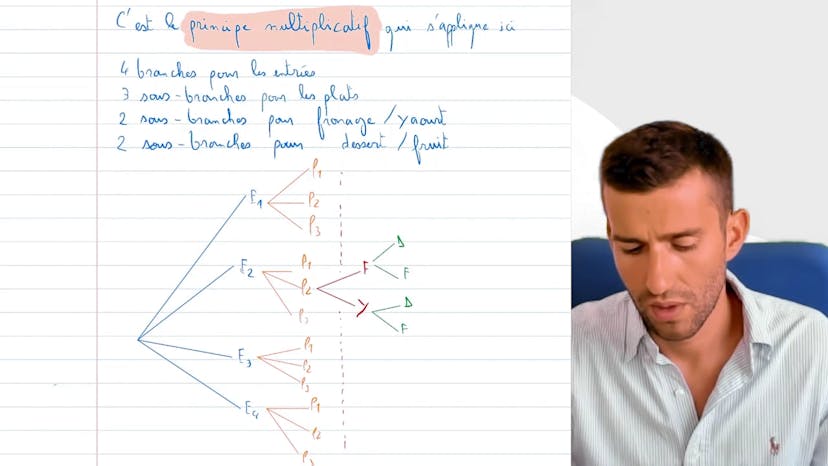
Dans cette vidéo, nous apprenons comment réaliser un arbre pondéré pour dénombrer le nombre de menus possibles dans une cantine scolaire. L'arbre pondéré est une méthode pratique, bien qu'elle demande du temps à réaliser. Il est recommandé de ne pas s'attarder sur cette méthode si le nombre de sous-branches devient trop important. Dans notre exemple, la cantine propose 4 entrées, 3 plats, et le choix entre fromage ou yaourt et entre dessert ou fruit. Pour déterminer le nombre de menus possibles, nous construisons un arbre avec ces différentes options. Cependant, pour simplifier, nous ne représentons pas toutes les combinaisons. En effet, avec 4 entrées, 3 plats, 2 choix de produits laitiers, et 2 choix de desserts ou fruits, cela ferait un total de 48 branches, ce qui devient fastidieux. Pour compter le nombre de menus possibles, nous utilisons le principe multiplicatif. Nous multiplions les possibilités de chaque catégorie : 4 (entrées) x 3 (plats) x 2 (choix de produits laitiers) x 2 (choix de desserts ou fruits), ce qui donne un total de 48 menus possibles. Il est important de noter que dans cet arbre, les pondérations ne sont pas prises en compte. Les pondérations seraient utilisées dans le contexte des probabilités, où différentes probabilités pourraient être attribuées à chaque choix. Cependant, cela ne fait pas partie de cette discussion et sera abordé dans un prochain chapitre.