 Tous les sujets
Tous les sujets Maths
Maths- Nombres et calculs
- Géométrie
- Fonctions
- Stats et Probas
- Analyse
- Géométrie
- Probas et Stats
- Analyse (spé)
- Géométrie (spé)
- Probabilités (spé)
- Arithmétique (exp)
- Complexes (exp)
- Analyse
- Algèbre
- Divisibilité et Congruences
- PGCD
- Théorèmes de Bézout et Gauss
- Nombres Premiers
- Complexes : vision algébrique
- Complexes : vision géométrique
- Rappels et Probas Conditionnelles
- Dénombrement : définitions
- Dénombrement : combinaisons
- Indépendance : méthodes
- Variable aléatoire et binomiale
- Loi usuelles, groupes
- Anneaux corps
- Analyse
- Algèbre
- Probabilités
SecondePremièreTerminale2BAC SM MarocMPSI/PCSI Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée Prépa Examens
Prépa Examens
Terminale
Première
Seconde
MPSI/PCSI
2BAC SM Maroc
 Tous les sujets
Tous les sujets Maths
Maths- Nombres et calculs
- Géométrie
- Fonctions
- Stats et Probas
- Analyse
- Géométrie
- Probas et Stats
- Analyse (spé)
- Géométrie (spé)
- Probabilités (spé)
- Arithmétique (exp)
- Complexes (exp)
- Analyse
- Algèbre
- Divisibilité et Congruences
- PGCD
- Théorèmes de Bézout et Gauss
- Nombres Premiers
- Complexes : vision algébrique
- Complexes : vision géométrique
- Rappels et Probas Conditionnelles
- Dénombrement : définitions
- Dénombrement : combinaisons
- Indépendance : méthodes
- Variable aléatoire et binomiale
- Loi usuelles, groupes
- Anneaux corps
- Analyse
- Algèbre
- Probabilités
SecondePremièreTerminale2BAC SM MarocMPSI/PCSI Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée Prépa Examens
Prépa Examens
Maths SM&SP
Algèbre
2BAC SM Maroc

Déterminer un PGCD
Dans cet exercice, l'objectif est de calculer le Plus Grand Commun Diviseur (PGCD) des nombres 18840 et 9828 en utilisant l'algorithme d'Euclide.
L'algorithme d'Euclide consiste en une série de divisions euclidiennes successives. On commence par diviser le plus grand nombre par le plus petit. Dans ce cas, 18840 peut être divisé par 9828 une fois, avec un reste de 9012.
Ensuite, on effectue la division euclidienne du diviseur précédent par ce reste. On répète ce processus jusqu'à obtenir un reste de 0.
Ainsi, 9828 divisé par 9012 donne un résultat de 1, avec un reste de 816. On continue avec cette division, donc 9012 divisé par 816 donne un résultat de 11, avec un reste de 36.
On répète une fois de plus, donc 816 divisé par 36 donne un résultat de 22, avec un reste de 24. On continue, 36 divisé par 24 donne un résultat de 1, avec un reste de 12.
Enfin, 24 divisé par 12 donne un résultat de 2, avec un reste de 0. Le reste de 0 indique que nous avons atteint un multiple commun.
En utilisant l'algorithme d'Euclide, le PGCD entre 18840 et 9828 est donc 12, qui correspond au dernier reste non nul obtenu.
Maths SM&SP
Algèbre
2BAC SM Maroc

Différence et quotient
Dans cet exercice, nous devons trouver deux nombres entiers dont la différence est égale à 538, et où le quotient de leur division est égal à 13, avec un reste de 34.
Pour résoudre ce problème, nous allons modéliser les deux entiers recherchés comme A et B, en supposant que A est plus grand que B. Nous pouvons le faire car la différence est de 538, ce qui signifie qu'ils ne sont pas égaux, et lorsqu'il y a deux nombres, l'un est forcément plus grand que l'autre.
Nous avons donc deux informations : la différence est de 538 (A - B = 538) et le quotient est de 13 (A = 13B + 34).
Nous allons résoudre ce système d'équations en soustrayant la première équation de la deuxième pour trouver B. Ainsi, nous avons A - A + B = 13B + 34 - 538, ce qui se simplifie en B = 42.
Maintenant que nous avons trouvé B, nous pouvons trouver A en remplaçant B dans la première équation. A - 42 = 538, ce qui donne A = 580.
Finalement, les deux nombres recherchés sont A = 580 et B = 42.
Maths SM&SP
Algèbre
2BAC SM Maroc
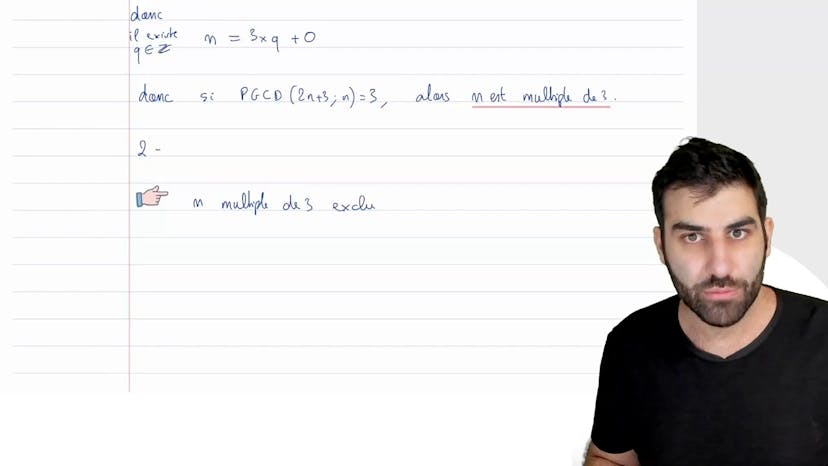
PGCD qui dépend de n
Dans cet exercice, on nous demande de déterminer l'ensemble des entiers naturels n pour lesquels le PGCD de 2n+3 et de n vaut 3. Pour résoudre cette question, on utilise l'algorithme d'Euclide en effectuant la division euclidienne de 2n+3 par n.
On remarque que 2n+3 est déjà divible par n, puisque 2n+3 = 2(n+1). Ainsi, 3 est le PGCD des deux nombres.
On peut donc en conclure que n est divisible par 3. Finalement, si le PGCD de 2n+3 et de n est égal à 3, cela signifie que n est un multiple de 3.
Ensuite, on nous demande de déduire l'ensemble des entiers naturels n pour lesquels le PGCD de 2n+3 et de n vaut 1. On remarque que si n est un multiple de 3, le PGCD est forcément 3 et non 1. Ainsi, nous devons exclure les multiples de 3.
Pour trouver les autres cas où le PGCD est 1, on considère que n peut s'écrire sous la forme 3k+2, où k est un entier naturel. On effectue alors la division euclidienne de 2n+3 par n. On trouve que le reste est 1. Le PGCD est donc égal à 1 lorsque n s'écrit sous la forme 3k+2.
On peut aussi considérer le cas où n s'écrit sous la forme 3k+1. En effectuant la division euclidienne de 2n+3 par n, on trouve également un reste de 1. Donc, le PGCD est égal à 1 lorsque n s'écrit sous la forme 3k+1.
Finalement, on peut conclure que si n n'est pas un multiple de 3, alors le PGCD de 2n+3 et de n vaut 1.
Maths SM&SP
Algèbre
2BAC SM Maroc

Autre dépendance en n
Dans cet exercice, nous devons déterminer le PGCD (Plus Grand Commun Diviseur) de deux entiers, a et b, qui dépendent de n. Les valeurs de a et b sont respectivement n + 4 et 3n + 7.
Pour résoudre ce problème, nous commençons par noter D comme le PGCD de a et b. Nous souhaitons nous débarrasser de la variable n pour nous concentrer uniquement sur le PGCD. Ainsi, nous utilisons une combinaison linéaire de a et b pour éliminer n. Étant donné que D divise a et b, il doit également diviser toute combinaison linéaire entière de ces deux nombres. Par conséquent, D divise également 3a - b.
En simplifiant cette expression, nous obtenons 3a - b = 5 (après avoir supprimé la variable n). Cette information est précieuse, car si D divise 5 et que 5 est un nombre premier, alors D ne peut être que 1 ou 5.
Nous examinons donc deux situations possibles :
- Si D est égal à 5, cela signifie que a est congru à 0 modulo 5 (c'est-à-dire que a est un multiple de 5). Étant donné que a est n + 4, cela implique que n est congru à 1 modulo 5.
- Si D est égal à 1, cela signifie que n n'est pas congru à 1 modulo 5.
Finalement, le PGCD de a et b est égal à 5 si et seulement si n est congru à 1 modulo 5, et il est égal à 1 si et seulement si n n'est pas congru à 1 modulo 5.
Maths SM&SP
Algèbre
2BAC SM Maroc
PGCD et n carré
Aucun résumé n'est disponible pour cette vidéo
Maths SM&SP
Algèbre
2BAC SM Maroc

PGCD et PPCM
Dans cet exercice, nous devons trouver deux nombres en utilisant le PGCD (Plus Grand Commun Diviseur) et le PPCM (Plus Petit Commun Multiple). Nous avons les informations suivantes : A est plus petit que B, le PGCD des deux nombres est égal à 6, et le PPCM est égal à 102.
Pour résoudre ce problème, nous devons rappeler qu'il existe une formule qui relie le produit de deux nombres à leur PGCD et leur PPCM. Cette formule indique que le produit de A et B est égal au produit de leur PGCD et leur PPCM.
Nous allons utiliser une propriété du PGCD pour trouver les valeurs de A et B. Il existe A' et B' tels que A est égal à 6 fois A' et B est égal à 6 fois B'. De plus, A' et B' sont premiers entre eux, ce qui signifie qu'ils n'ont pas de diviseurs communs autres que 1.
Si nous utilisons cette formule avec les valeurs de A et B données, nous avons 6 fois A' fois 6 fois B' est égal à 6 fois 102, ce qui simplifie en A'B' égal à 17.
Comme 17 est un nombre premier et que A' est plus petit que B', nous pouvons conclure que A' est égal à 1 et B' est égal à 17. Cependant, nous recherchons les valeurs de A et B, donc nous utilisons cela pour trouver que A est égal à 6 (6 fois 1) et B est égal à 17 fois 6, soit 102.
Donc, les nombres que nous cherchons sont A = 6 et B = 102.
Maths SM&SP
Algèbre
2BAC SM Maroc

PGCD et congruences
Salut ! Dans cet exercice, nous devons démontrer une équivalence entre deux systèmes de congruence. Le premier système nous dit que n est congruent à 1 modulo 5 et congruent à 5 modulo 7. Pour montrer que si n satisfait ce système, alors il satisfait également l'autre système, nous manipulons les congruences.
Pour la première congruence, n congruent à 1 modulo 5, nous nous intéressons à 4n plus 1 modulo 5. En multipliant cette expression par 4, nous obtenons que 4n est congruent à 4 modulo 5. Comme 4 est équivalent à -1 modulo 5, nous remplaçons 4 par -1. Ainsi, nous obtenons que 4n plus 1 est congruent à 0 modulo 5.
Pour la deuxième congruence, si n est congruent à 5 modulo 7, alors 4n est congruent à 20 modulo 7. Comme 20 est équivalent à -1 modulo 7, nous remplaçons 20 par -1. Donc 4n plus 1 est congruent à 0 modulo 7.
En utilisant le corollaire du théorème de Gauss, qui dit que si A divise C, B divise C, et que le PGCD de A et B vaut 1, alors AB divise C, nous pouvons déduire que 4n plus 1 est congruent à 0 modulo 35. Cela est possible car 5 et 7 sont premiers entre eux.
Maintenant, pour trouver les solutions du système S, nous utilisons l'information précédente selon laquelle 4n est congruent à -1 modulo 35. Nous devons trouver une valeur k dans les entiers de 1 à 35 telle que 4k est congruent à 1 modulo 35. En multipliant chaque côté par 9, nous trouvons que 4n est congruent à -9 modulo 35. Ainsi, n est congruent à 26 modulo 35.
En résumé, les solutions du système S sont tous les nombres de la forme 26 plus 35k, avec k appartenant à Z.
Maths SM&SP
Algèbre
2BAC SM Maroc

PGCD et Suite
Dans cet exercice, on nous parle de deux suites : u et v. La suite u est définie par u0 = 0, u1 = 1, et la relation de récurrence un+2 = 3un+1 - 2un. La suite v est définie par vn = un+1 - un. On nous demande de montrer que la suite v est une suite géométrique et de déterminer sa raison et son premier terme.
Pour montrer que la suite v est géométrique, on calcule vn+1 et on essaye de l'écrire comme quelque chose fois vn. En effectuant les calculs, on obtient que vn+1 = 2vn. Donc la suite v est bien géométrique avec une raison de 2 et son premier terme est v0 = 1.
Ensuite, on nous demande de déduire que pour tout entier n, un est un entier naturel et que un+1 = 2(un+1). Cette question peut sembler étrange car on parle de la suite v et ensuite on demande de déduire quelque chose à partir de cette question. Cependant, on remarque que la suite v est construite de manière particulière : vn est la différence entre deux termes consécutifs de la suite u. On peut donc penser à une somme télescopique pour trouver des informations sur un et un+1.
En effectuant la somme des termes de la suite v, on obtient que la somme de vn pour k allant de 0 à n est égale à un+1. Or, la suite v étant géométrique, on connaît une formule pour calculer la somme d'une suite géométrique : v0(1-q^n+1)/(1-q), où v0 est le premier terme de la suite v, q est la raison et n est le nombre de termes. En remplaçant par les valeurs connues, on trouve que la somme des termes de v est égale à 2^(n+1) - 1. Donc un+1 = 2^(n+1) - 1. Cela signifie que pour tout entier naturel n, un est un entier.
On nous demande également de vérifier que un+1 = 2un+1. En substituant un par 2^(n+1) - 1 dans cette équation, on obtient bien l'égalité.
Enfin, on déduit que deux termes consécutifs de la suite u sont premiers entre eux. Pour le prouver, on utilise le théorème de Bézout qui dit qu'une combinaison linéaire de deux entiers donne le PGCD de ces entiers. On a montré précédemment que un+1 = un - 2un. Donc en passant un+1 de l'autre côté de l'équation, on obtient que le PGCD de un et un+1 est égal à un. Donc les termes consécutifs de la suite u sont bien premiers entre eux.
Maths SM&SP
Algèbre
2BAC SM Maroc
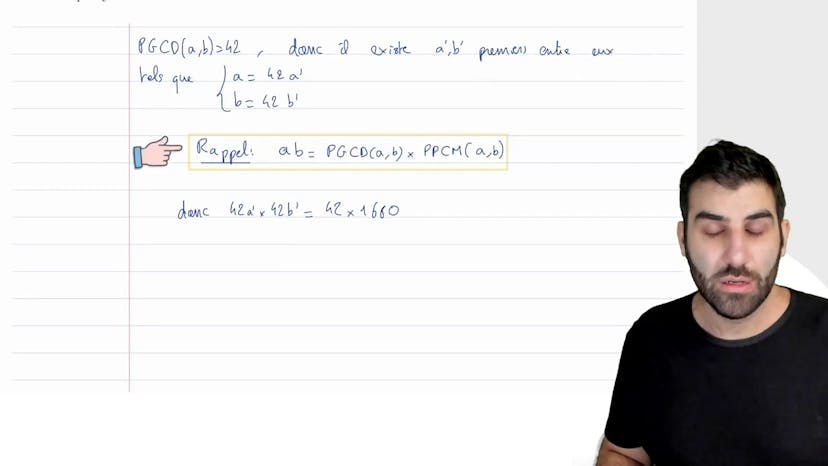
PGCD+PPCM
Dans cet exercice, nous cherchons un couple de nombres A et B tels que leur PGCD est égal à 42 et leur PPCM est égal à 1680. Nous commençons par utiliser la propriété qui dit que le PGCD de deux nombres peut être exprimé en utilisant des diviseurs premiers. Ainsi, nous pouvons écrire A comme étant égal à 42 multiplié par A' et B comme étant égal à 42 multiplié par B'. En utilisant cette simplification, nous pouvons ensuite appliquer la formule qui dit que le produit de deux nombres est égal au produit de leur PGCD et de leur PPCM. En remplaçant A et B par leur formulation simplifiée, nous obtenons l'équation 42A' * 42B' = 42 * 1680. Après simplification, nous obtenons A' * B' = 40. Puisque A' et B' sont des diviseurs de 40 et qu'ils doivent être premiers entre eux, les seules possibilités sont A' = 1 et B' = 40, ou A' = 5 et B' = 8. En utilisant ces valeurs, nous obtenons finalement les solutions A = 42 et B = 1680, ou A = 210 et B = 336 pour le système d'équations du PGCD et du PPCM.


