Cours de Fonctions : dérivabilité (2) en Ligne par les Meilleurs Professeurs - Fonctions : dérivabilité (2)

En construction !

Aucun résumé n'est disponible pour cette vidéo

Mathématiques

ECG

En construction !

Aucun résumé n'est disponible pour cette vidéo

Mathématiques

BCPST

En construction !

Aucun résumé n'est disponible pour cette vidéo

Dans ce cours, nous allons voir comment utiliser le théorème de Rolle de manière efficace. Le théorème de Rolle se présente sous forme d'exercices, notamment avec une petite astuce pas facile à comprendre. Pour commencer, nous considérons une fonction f définie sur un intervalle i, de classe Cn, qui s'annule en n plus un point distinct de i. Nous voulons montrer que la dérivée n s'annule au moins une fois sur i, puis que la dérivée n-1 de f'αf s'annule également au moins une fois sur i. La première méthode consiste à utiliser la récurrence. Nous démontrons la propriété suivante pk : la dérivée km s'annule n plus une moins k fois au moins sur i. Pour l'initialisation, nous n'avons pas de problème. Par hypothèse, fk s'annule n plus une moins k fois. Nous voulons montrer que la dérivée k plus unième s'annule n moins k fois au moins. Nous appliquons le théorème de Rolle sur chaque intervalle ij défini par les points αj et αj plus 1. Ainsi, nous avons n moins k intervalles sur lesquels la dérivée s'annule au moins une fois. En utilisant le théorème de Rolle, nous démontrons que fk plus 1 s'annule au moins n moins k fois. Cette démonstration par récurrence fonctionne parfaitement. Pour la question 2, nous introduisons une fonction h qui est égale à f de x multiplié par e de alpha x. En dérivant h, nous obtenons h prime qui est égal à f prime plus alpha f fois e de alpha f. L'astuce ici est que nous pouvons appliquer le théorème de Rolle sur chaque point où h s'annule, car si h prime s'annule au moins une fois, cela signifie que le terme f prime plus alpha f s'annule également au moins une fois. En utilisant les hypothèses précédentes, nous appliquons le théorème de Rolle et retrouvons que la dérivée enième de f prime plus alpha f s'annule au moins une fois. Ainsi, nous pouvons utiliser le théorème de Rolle dans des exercices en utilisant une petite astuce pour simplifier la démonstration.

Formule de Taylor Lagrange

Le cours traite de la notion de point fixe dans le cadre de suites définies par récurrence et de fonctions définies en escalier. Il explique comment déterminer si un point est récursif ou attractif en se basant sur certaines propriétés de la fonction dérivée. L'astuce utilisée est de poser g(x) = f(x) - x et d'appliquer le théorème des accroissements finis pour prouver l'unicité du point fixe. Ensuite, il démontre que dans une suite définie par récurrence, les termes convergent vers le point fixe en utilisant une démonstration par récurrence. Enfin, il explique que le caractère attractif du point fixe dépend de la pente de la fonction, qui doit être inférieure à 1. Le cours se termine en soulignant l'importance de cette notion dans la résolution d'exercices et d'épreuves.

Règle de l’Hopital

La règle de l'hôpital est un théorème mathématique intéressant qui n'est pas enseigné en France, mais qui est au programme dans certains pays tels que l'Angleterre ou le Luxembourg. Ce théorème permet de calculer la limite d'une fonction indéterminée en utilisant les dérivées des fonctions en question. Pour appliquer cette règle, il faut que les fonctions soient continues et dérivables sur un intervalle donné. Le théorème des accroissements finis généralisé est utilisé pour démontrer la règle de l'hôpital. Il permet de calculer la dérivée d'une fonction composée de deux autres fonctions. Grâce à cette démonstration, on peut ensuite appliquer la règle de l'hôpital à des exemples concrets. La règle de l'hôpital est utile lorsqu'on se retrouve avec une forme indéterminée dans le calcul d'une limite. Elle permet de remplacer une fonction indéterminée par une autre fonction dont la limite est connue. Deux exemples sont donnés pour illustrer l'utilisation de la règle de l'hôpital. Dans le premier exemple, on calcule la limite d'une fonction (x-sin(x))/x^3 en utilisant la règle de l'hôpital. Dans le deuxième exemple, on calcule la limite d'une fonction ln(1+x)-x/x^2 en utilisant également la règle de l'hôpital. Il est précisé que les développements limités sont utilisés pour simplifier les calculs dans ces exemples, mais que leur compréhension complète nécessite des connaissances supplémentaires. En conclusion, la règle de l'hôpital est un outil puissant pour calculer des limites de fonctions indéterminées, mais elle n'est pas enseignée en France. Cependant, il est possible d'avoir à la démontrer dans un exercice, comme cela a été fait dans cet cours.

Polynome de Legendre

Les polynômes de Legendre sont une famille de polynômes qui se montrent sous la forme Pn(x) = (dérivée énième de x²-1 à la puissance n). Ces polynômes ont un degré de 2n et ont un coefficient dominant de (2n factorial / n factorial). En examinant la dérivée de Pn, on peut déterminer les racines du polynôme, notamment les racines d'ordre n-k et les racines d'ordre 1. En appliquant le théorème de Rolle, on peut montrer que Pn a n points distincts d'annulation. Les polynômes de Legendre sont souvent rencontrés dans le domaine des polynômes et il est important de retenir leur forme et leurs propriétés.

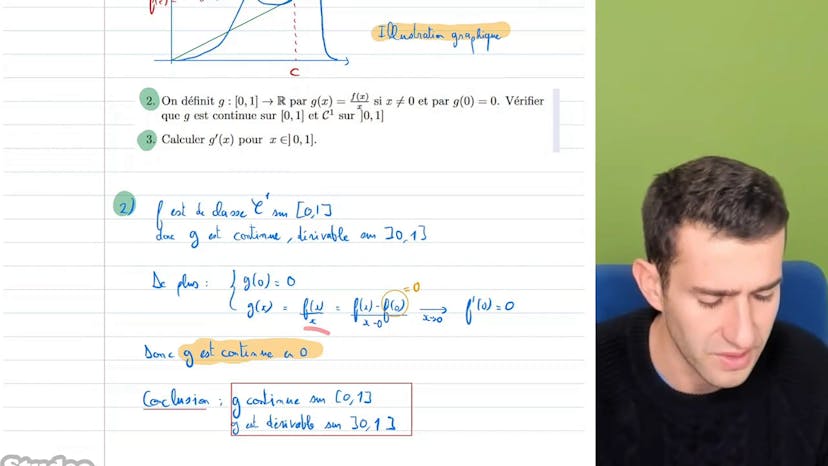
Corde et tangente

Dans cet exercice, on cherche à démontrer qu'il existe un certain point où la corde et la tangente d'une fonction sont confondues. Pour cela, nous étudions une fonction f qui vérifie certaines conditions : elle est définie de 0 à 1 dans R, continue et dérivable (de classe c1), et f(0) = f'(0) = f'(1) = 0. On commence par rappeler l'équation de la tangente et de la corde au point c de la courbe. La tangente est représentée par une droite qui passe par le point m de la courbe et a une pente égale à la dérivée de f au point c. La corde est une droite reliant le point m au point o, avec une pente égale à f(c)/c. Pour que la corde et la tangente soient confondues, elles doivent passer par le même point m et avoir la même pente. Ainsi, on cherche un point c où f'(c) = f(c)/c. On introduit une fonction auxiliaire g(x) = f(x)/x et on montre qu'elle est continue sur [0,1] et de classe c1 sur ]0,1[. Si f(1) = 0, alors c = 1 convient car f(c) = f(1) = 0 et f'(c) = f'(1) = 0. Si f(1) > 0, on calcule g(0), g(1) et g'(1). On a g(0) = 0, g(1) = f(1)/1 > 0 et g'(1) = f'(1) - f(1) < 0. On en déduit que g'(x) s'annule sur ]0,1[, ce qui signifie qu'il existe un point c compris entre 0 et 1 où f'(c) = f(c)/c. Si f(1) < 0, on applique le même raisonnement en changeant les signes. On trouve également un point c où f'(c) = f(c)/c. En résumé, dans les conditions données (f(0) = f'(0) = f'(1) = 0), on a démontré qu'il existe un point c dans [0,1] où la corde et la tangente de la fonction f sont confondues.

En construction !

Aucun résumé n'est disponible pour cette vidéo

Théorème de Rolle

Bienvenue à tous ! Dans ce cours, nous allons voir comment bien utiliser le théorème de Rolle en SEO friendly. Le théorème de Rolle est utilisé lorsque l'on souhaite montrer que la dérivée d'une fonction s'annule au moins une fois sur un intervalle donné. Pour cela, on considère une fonction f définie sur un intervalle i, de classe Cn, et qui s'annule en n plus un point distinct de i. La première méthode pour démontrer cela est par récurrence. On montre ainsi que la dérivée km s'annule n plus une moins k fois au moins sur i. Dans cette démonstration, on applique le théorème de Rolle sur des intervalles spécifiques, ce qui permet de montrer que la dérivée s'annule au moins une fois sur ces intervalles. On peut continuer ainsi jusqu'à obtenir que la dérivée enième de f s'annule au moins une fois. Dans la seconde partie du cours, on aborde une astuce un peu plus complexe. On pose une fonction h qui est le produit de f par l'exponentielle de alpha x. En dérivant cette fonction, on obtient f' + alpha f fois l'exponentielle de alpha x. L'astuce ici est que, comme l'exponentielle est toujours positive, si h s'annule au moins une fois, cela signifie que le terme f' + alpha f s'annule lui aussi au moins une fois. Ainsi, on peut appliquer le théorème de Rolle sur h prime et montrer que la dérivée enième de f' + alpha f s'annule au moins une fois. Voilà comment bien utiliser le théorème de Rolle dans des exercices, en utilisant ces petites astuces pour démontrer que les dérivées s'annulent sur les intervalles donnés.

Formule de Taylor Lagrange

Dans ce cours, nous allons étudier le concept de point fixe en mathématiques. Un point fixe est une solution de l'équation f(x) = x, où f est une fonction dérivable sur un intervalle ab. Pour qu'un point fixe existe et soit unique, il faut que la dérivée de f soit inférieure en valeur absolue à une constante k appartenant à (0,1). Pour prouver l'existence d'un point fixe, nous utilisons un résultat classique en mathématiques. Nous posons g(x) = f(x) - x et nous montrons que g(a) > 0 et g(b) < 0, où a et b sont les bornes de l'intervalle ab. En utilisant le théorème des valeurs intermédiaires, nous concluons qu'il existe au moins un point fixe gamma tel que g(gamma) = 0. Ensuite, nous démontrons l'unicité du point fixe. Supposons qu'il existe deux points fixes gamma1 et gamma2 distincts. En utilisant le théorème des inégalités des accroissements finis, nous montrons que la différence entre gamma1 et gamma2 est strictement inférieure à gamma1 - gamma2, ce qui est impossible. Donc, nous concluons que gamma1 = gamma2, c'est-à-dire qu'il n'existe qu'un seul point fixe. Enfin, nous étudions la convergence vers le point fixe. Nous considérons une suite u(n) définie par récurrence, avec u(0) dans l'intervalle ab, et nous montrons que |u(n) - gamma| est inférieure à k^n |u(0) - gamma|. Puisque k est strictement inférieur à 1 en valeur absolue, la suite u(n) converge vers le point fixe gamma. Pour mieux comprendre le caractère attractif du point fixe, nous utilisons des graphiques. Si la pente de la fonction f est inférieure à 1 sur tout l'intervalle ab, alors la suite u(n) converge rapidement vers le point fixe. Si la pente est supérieure à 1, la suite fuirait plutôt le point fixe. En conclusion, le théorème du point fixe est un résultat classique en mathématiques et peut être utilisé pour résoudre des exercices et des problèmes. Il permet de démontrer l'existence, l'unicité et la convergence des points fixes d'une fonction dérivable.

Règle de l’Hopital

Dans cette vidéo, on aborde la règle de l'hôpital, un théorème intéressant mais qui n'est pas enseigné dans le programme français. Cependant, dans d'autres pays comme l'Angleterre et le Luxembourg, il est au programme de terminale. Ce théorème s'applique lorsque l'on a deux fonctions f et g continues et dérivables sur un intervalle a, b. On suppose qu'il existe un point x0 où les deux fonctions s'annulent, et que la dérivée de g ne s'annule pas ailleurs dans cet intervalle. La règle de l'hôpital affirme que si la limite de f' sur g' quand x tend vers 0 tend vers l, alors la limite de f sur g quand x tend vers 0 tend vers l également. Pour démontrer ce théorème, on utilise le théorème des accroissements finis généralisé, qui lui est au programme. On crée une fonction h qui est égale à une expression comprenant les fonctions f et g. En calculant sa dérivée, on peut montrer que ce théorème s'applique. On utilise alors ce théorème dans deux exemples spécifiques pour montrer l'efficacité de la règle de l'hôpital. En résumé, la règle de l'hôpital est un théorème qui permet de calculer des limites de fonctions indéterminées. Bien que ce théorème ne fasse pas partie du programme français, il peut être appliqué dans des exercices pour simplifier les calculs.

Polynome de Legendre

Les polynômes de Legendre sont une famille de polynômes qui se présentent sous la forme Pn(x) = (d^n/dx^n)(x^2-1)^n. Ils sont étudiés dans le contexte des dérivés et ont un degré de 2n avec un coefficient dominant de 2n! / n!. Les racines de ces polynômes sont étudiées en utilisant le théorème de Rolle, qui montre que les racines sont distinctes et se situent entre -1 et 1. Cette propriété permet de conclure que les polynômes de Legendre ont n racines distinctes. Les polynômes de Legendre sont souvent rencontrés dans le chapitre sur les polynômes et leur forme doit être retenue car elle revient souvent.

Corde et tangente

Bonjour à tous ! Aujourd'hui, nous allons aborder la méthode des cordes et des tangentes dans le cadre de fonctions. Nous découvrirons que dans certaines conditions, il est possible de trouver une tangente et une corde communes. L'exercice que nous allons traiter propose une fonction vérifiant plusieurs caractéristiques : elle est définie de 0 à 1 dans R, est de classe c1 et vérifie f(0) = f'(0) = f'(1) = 0. Notre objectif est de montrer qu'il existe un point c appartenant à l'intervalle [0,1] tel que f'(c) = f(c)/c. Pour commencer, nous devons comprendre ce que cela représente géométriquement. Si nous prenons un élément c dans l'intervalle [0,1] et le point m sur la courbe correspondant à ce c, nous devons rappeler l'équation de la tangente en ce point ainsi que celle de la corde reliant le point (0,f(0)) au point (c,f(c)). Notre but est de donner une interprétation géométrique de ce résultat. En général, la corde entre les points m et o (0,f(0)) correspond à la droite verte dans notre dessin, tandis que la tangente est la droite passant par le point m et ayant une pente égale à la dérivée de la fonction en ce point. Donc, les pentes de ces droites sont respectivement f'(c) pour la tangente et f(c)/c pour la corde (dans le cas où f(0) = 0). Notre objectif est de trouver un point où la corde et la tangente se confondent, c'est-à-dire où ces deux droites passent par le même point et ont la même pente. En d'autres termes, nous cherchons un point où la corde et la tangente coïncident. Maintenant que nous comprenons cela, examinons les équations de la tangente et de la corde. L'équation de la tangente est y = f'(c)*(x-c) + f(c), tandis que l'équation de la corde est y = f(c)/c * x. Si nous simplifions ces expressions, nous obtenons les formes ax + b, avec a et b correspondant aux coefficients directs et à l'ordonnée à l'origine respectivement. Pour que ces deux droites soient égales, elles doivent avoir les mêmes coefficients directs et les mêmes ordonnées à l'origine. Ainsi, ces deux équations aboutissent à la condition suivante : f'(c) = f(c)/c. C'est ce que nous cherchons à prouver. Dans notre dessin, nous avons choisi les bonnes caractéristiques : f(0) = 0, f'(1) = 0 et f'(0) = 0. Le point c que nous cherchons se trouve ici, où la tangente et la corde se confondent. Pour continuer, nous introduisons une fonction auxiliaire f(x)/x et nous devons montrer qu'elle est continue sur l'intervalle [0,1] et de classe c1 sur l'intervalle ouvert (0,1). Comme f est de classe c1 sur [0,1], elle l'est également sur (0,1) en faisant attention au problème en 0 dû à la division par x. En posant g(0) = 0, nous vérifions sa continuité en 0. En dehors de 0, il n'y a aucun problème pour la continuité. La question suivante consiste à calculer g'(x) pour tout x dans (0,1). Nous utilisons les théorèmes de dérivation classiques pour calculer g'(x) = f'(x) - f(x)/x^2. Nous avons alors deux cas à examiner : lorsque f(1) = 0 et lorsque f(1) > 0. Dans le premier cas, c=1 convient car f(c) = f(1) = 0 et f'(c) = f'(1) = 0, ce qui satisfait notre équation recherchée f'(c) = f(c)/c. Dans le second cas, nous devons calculer g(0), g(1) et g'(1). Nous avons g(0) = 0, g(1) = f(1)/1 > 0 et g'(1) = -f(1) < 0. Nous en déduisons que g' s'annule sur [0,1]. En appliquant le théorème de Rolle sur g', nous trouvons qu'il existe un c entre 0 et 1 tel que g'(c) = 0. En reprenant notre calcul de g'(x), nous obtenons l'équation recherchée f'(c) = f(c)/c. En conclusion, nous avons répondu au problème en prenant en compte les hypothèses suivantes : f(0) = f'(0) = f'(1) = 0. Dans ce cas, nous avons pu montrer qu'il existe un point c où la corde et la tangente sont confondues. C'est ainsi que se conclut cet exercice.

Théorème de Darboux

Dans ce cours, nous avons examiné une méthode pour démontrer le théorème de Darboux, qui est une extension du théorème des valeurs intermédiaires. Nous avons d'abord noté qu'il n'est pas trivial de prouver ce théorème, car la fonction dérivée n'est pas nécessairement continue. Ensuite, nous avons supposé que f'(A) est inférieur à f'(B), avec un réel Z compris entre les deux. Nous avons ensuite utilisé la notion de limite pour construire notre raisonnement. Nous avons montré que si une fonction est dérivable en A, alors le taux d'accroissement tend vers f'(A). En utilisant cette propriété, nous avons trouvé un epsilon qui nous permet de prouver que Z est compris entre les taux d'accroissement en A et B. Ensuite, nous avons montré qu'il existe un point Y tel que le taux d'accroissement en ce point soit égal à Z. Enfin, nous avons utilisé le théorème des accroissements finis pour montrer que Z appartient à l'intervalle des taux d'accroissement en Y. En résumé, nous avons montré que si f'(A) est inférieur à f'(B), alors tout réel Z appartenant à l'intervalle de f'(A) à f'(B) appartient à f'(Y), où Y est un point compris entre A et B. Nous avons appliqué cette méthode à une fonction spécifique, x²sin(1/x²), pour montrer que f est dérivable mais que f' n'est pas continue sur l'intervalle ouvert (0,1).

Théorème du point fixe

Bonjour à tous ! Aujourd'hui, nous allons parler du point fixe en mathématiques, plus précisément des points attractifs. Nous avons une fonction f qui est dérivable sur l'intervalle [a, b], et nous supposons qu'il existe une constante k appartenant à [0, 1] telle que la dérivée de f soit inférieure en valeur absolue à k. Un point fixe est une solution gamma telle que f(gamma) = gamma. Tout d'abord, nous montrons que ce point fixe est unique. Pour cela, nous posons g(x) = f(x) - x et utilisons le théorème des valeurs intermédiaires (TVI) pour montrer qu'il existe au moins un point fixe. Ensuite, nous supposons qu'il y en a deux et utilisons le théorème des inégalités des accroissements finis (IAF) pour montrer qu'ils sont identiques. Ensuite, nous considérons une suite définie par récurrence et souhaitons montrer qu'elle converge vers le point fixe gamma. Pour cela, nous utilisons à nouveau l'IAF pour encadrer u(n) - gamma et démontrer que cette suite converge vers 0, ce qui implique que u(n) converge vers gamma. En conclusion, nous avons vu que le point fixe est unique, qu'il est attractif et comment utiliser le théorème du point fixe dans des exercices.