Essai gratuit

Tous les sujets

Terminale

Première

Seconde

MPSI/PCSI

2BAC SM Maroc

Level

Tous les sujets

Terminale

Première

Seconde

MPSI/PCSI

2BAC SM Maroc

Level

Révisions Maths lycée

Analyse Terminale

MPSI/PCSI

Composition : Déf

Dans cette vidéo, l'auteur explique ce qu'est la composition de deux fonctions en utilisant des exemples concrets. Il commence par décomposer une fonction en plusieurs étapes, en partant de x. Il explique que chaque étape consiste en une transformation de la fonction précédente. Par exemple, pour la fonction racine de x² plus 7, il passe successivement de x à x², puis de x² à x² plus 7, et enfin à la racine de x² plus 7. Il explique que cela revient à composer la variable x par trois fonctions simples. Ensuite, l'auteur donne une définition théorique de la composition de fonctions. Il explique que si on a deux fonctions U et V, où U est définie sur un intervalle i et à valeur dans un intervalle j, et V est définie sur j et à valeur dans un intervalle k, alors la composition de U et V, notée VU, est définie comme V de U de x. Autrement dit, on applique d'abord U à x, puis V au résultat obtenu. L'auteur mentionne également quelques propriétés de la composition de fonctions. Il explique que la composition de fonctions est associative, c'est-à-dire que (UV)W est égal à U(VW). Cependant, il précise que la composition de fonctions n'est pas commutative, c'est-à-dire que VU est généralement différent de UV. Pour illustrer cela, il donne l'exemple de deux fonctions U et V, où U est la fonction x² moins 7 et V est la fonction exponentielle. Il montre que VU et UV donnent des résultats différents, en prenant la valeur en 0 comme exemple. L'auteur conclut en rappelant l'importance de se rappeler que la composition de fonctions n'est pas commutative. Il encourage les spectateurs à poser des questions s'ils en ont, et les invite à se retrouver sur le forum pour discuter.

Révisions Maths lycée

Analyse Terminale

MPSI/PCSI

Dériver une composée

Dans cette vidéo, nous apprenons comment dériver une fonction composée. Nous commençons par expliquer ce qu'est la composition et les contraintes liées aux ensembles d'arrivée et de départ des fonctions composées. Ensuite, nous abordons les exemples les plus simples pour mieux comprendre le sujet. Par exemple, nous étudions la dérivée de 1/x et constatons que 1/u' ne correspond pas à la bonne formule, mais plutôt à -u'/u^2. Nous poursuivons avec d'autres exemples tels que la dérivée de racine de x et montrons que la bonne formule est (u'/2√u). Nous rappelons également les formules de dérivées de base, en insistant sur le fait qu'il faut toujours multiplier par u' lorsqu'il s'agit d'une fonction composée. 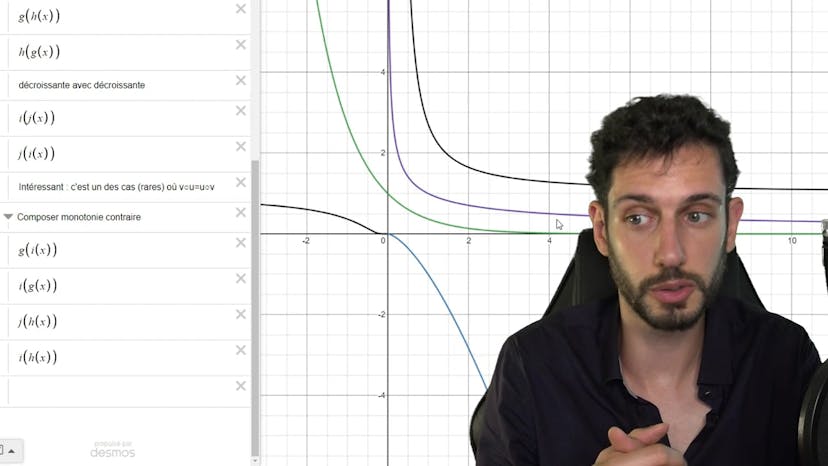Ensuite, nous donnons une définition formelle de la dérivée d'une fonction composée en utilisant les dérivées des fonctions u et v et en n'oubliant pas de multiplier par u'. Nous soulignons également qu'une conséquence intéressante est que si u et v ont la même monotonie, alors la fonction composée v∘u est croissante, tandis que si elles ont des monotonies contraires, la fonction composée est décroissante. Enfin, nous illustrons ces concepts avec des exemples concrets et montrons comment la monotonie des fonctions u et v affecte la monotonie de la fonction composée.

Révisions Maths lycée

Analyse Terminale

MPSI/PCSI

Fonction Composée

Dans ce cours, nous étudions une fonction composée et comment faire l'étude et le tableau de variation d'une fonction qui est composée de deux autres fonctions. Dans cet exemple, la fonction proposée est E2-1 sur x². Nous identifions les fonctions composantes de la fonction, g et h. La fonction g est -1 sur x², définie et dérivable sur R, tandis que la fonction h est l'exponentielle, définie et dérivable sur R. Nous utilisons les formules de dérivation pour trouver la dérivée de g, qui est 2 sur x³. Nous déterminons les variations de g en utilisant le signe de sa dérivée. Ainsi, on obtient un tableau de variation de g, qui est décroissante de moins l'infini à 0 et croissante de 0 à plus l'infini. Nous calculons également les limites de la fonction g, qui sont 0 en moins l'infini et moins l'infini en 0+. Ensuite, nous analysons la fonction h, qui est croissante sur R. En combinant les sens de variation de g et h, nous pouvons déduire les variations de la fonction composée, F. F sera donc décroissante sur R étoile moins et croissante sur R étoile plus. Nous calculons également les limites de F en utilisant les limites des fonctions composantes. La limite de F en moins l'infini est 1 et en plus l'infini est également 1. En 0, la limite de F est 0. Enfin, nous construisons le tableau de variation de F, qui est décroissante de 1 à 0 et croissante de 0 à 1. La fonction n'est pas définie en 0, mais peut être prolongée par continuité en posant F de 0 égale à 0. Une autre méthode aurait été de calculer directement la dérivée de F, mais nous avons choisi ici d'étudier l'intérieur de la composition. Si vous avez des questions, n'hésitez pas à les poser sur la FAQ.

Révisions Maths lycée

Analyse Terminale

BCPST

Composition : Déf

La vidéo explique le concept de composition de deux fonctions. Le professeur utilise un exemple concret pour illustrer la décomposition de la fonction racine de x² plus 7 en plusieurs étapes. Il explique que la fonction a subi trois transformations pour arriver à sa forme finale. Il donne également une définition plus théorique de la composition de fonctions et explique que la composition n'est pas commutative. Il souligne l'importance de se rappeler de cette propriété. En conclusion, il encourage les spectateurs à poser des questions sur le forum et annonce la prochaine vidéo.

Révisions Maths lycée

Analyse Terminale

BCPST

Dériver une composée

Dans cette vidéo, nous allons voir comment dériver une fonction composée. Nous avons déjà vu la notion de composition en première année, mais nous allons maintenant approfondir cette théorie. La dérivation d'une fonction composée peut sembler complexe, mais nous allons commencer par des exemples simples. Prenons par exemple la fonction u dérivable et le réel x. Nous savons que la dérivée de 1/x est -1/x^2. On pourrait donc penser que la dérivée de 1/u est -1/u^2. Cependant, il ne faut pas oublier le facteur u' dans la formule. La bonne formule est donc 1/u' = -u'/u^2. Reprenons avec la racine carrée de x. La dérivée de √x est 1/(2√x). On pourrait donc penser que la dérivée de √u est 1/(2√u). Mais encore une fois, il ne faut pas oublier le facteur u'. La bonne formule est u'/2√u. La règle générale qui se dégage est que dans la dérivation d'une fonction composée, il faut toujours multiplier par la dérivée de la fonction interne. La définition formelle de la dérivée d'une fonction composée est la suivante : soit u et v deux fonctions dérivables, alors la dérivée de v composée avec u est égale à la dérivée de v appliquée à u, multipliée par la dérivée de u. Une conséquence intéressante de cette règle est que si v et u ont la même monotonie, c'est-à-dire qu'elles sont soit croissantes, soit décroissantes, alors la fonction composée v composée avec u est croissante. En revanche, si v et u ont des monotonies opposées, alors la fonction composée est décroissante. En conclusion, la dérivation d'une fonction composée requiert de multiplier par la dérivée de la fonction interne. Il est important de ne pas oublier ce facteur lors de la dérivation. Vous pouvez vous entraîner avec les vidéos de méthodes pour bien comprendre cette partie du cours.

Révisions Maths lycée

Analyse Terminale

BCPST

Fonction Composée

Dans cette vidéo, nous étudions une méthode pour trouver le tableau de variation d'une fonction composée de deux autres fonctions. Nous prenons l'exemple de la fonction E2-1 sur x². Tout d'abord, nous identifions les fonctions qui composent la fonction E2-1 sur x². Nous avons la fonction g qui est égale à -1 sur x² et la fonction h qui est l'exponentielle. Nous notons que h est définie et dérivable sur R, tandis que g est définie et dérivable sur R* (excepté en 0). En utilisant les formules de dérivation, nous trouvons que la dérivée de g, notée g', est égale à 2 sur x³. Nous remarquons que g' est du signe de x. En utilisant cette information, nous déterminons les variations de g et dressons son tableau de variation, qui indique que g est décroissante de -∞ à 0 et croissante de 0 à +∞. Ensuite, nous trouvons les limites de g et les ajoutons au tableau de variation. En particulier, pour les limites en plus et moins l'infini ainsi qu'en 0, nous utilisons les propriétés de g pour déduire les valeurs des limites. Une fois que nous avons toutes les limites, nous dressons le tableau de variation complet pour la fonction composée. Nous mentionnons également que la fonction est paire, ce qui nous permet de déduire les variations sur R1 par parité. Ensuite, nous examinons le sens de variation de la fonction F en nous intéressant à la fonction H. Nous notons que la fonction exponentielle est croissante sur R et nous utilisons le tableau de variation de H pour déterminer les intervalles sur lesquels F est décroissante et ceux sur lesquels elle est croissante. En ce qui concerne les limites de F, nous utilisons les propriétés des fonctions composées pour déterminer les limites en moins et plus l'infini, ainsi qu'en 0. Enfin, nous traçons le tableau de variation de F en utilisant toutes les informations que nous avons recueillies. Nous notons que la fonction n'est pas définie en 0, mais nous pourrions prolonger la fonction par continuité en posant F de 0 égale à 0. En conclusion, cette méthode nous permet d'étudier le sens de variation d'une fonction composée sans nécessairement calculer la dérivée de la fonction.

Révisions Maths lycée

Analyse Terminale

ECG

Composition : Déf

La vidéo explique le concept de la composition de deux fonctions. L'exemple utilisé est la fonction "racine de x² plus 7". La fonction est décomposée en trois étapes : passer de x à x², puis de x² à x² plus 7, et enfin prendre la racine de x² plus 7. Les trois fonctions appliquées à x sont : la fonction carré, la fonction qui ajoute 7, et la fonction racine. Cette décomposition permet de composer la fonction en trois étapes. Ensuite, la vidéo donne une définition théorique de la composition de fonctions. Elle explique que la composition de deux fonctions est associative (c'est-à-dire que (UV)W est égal à U(VW)), mais elle n'est pas commutative (c'est-à-dire que UV est en général différent de VU). Elle donne l'exemple de deux fonctions, l'une étant une parabole et l'autre une exponentielle, pour illustrer cette non-commutativité. Finalement, la vidéo conseille de se rappeler que la composition de fonctions n'est pas commutative et encourage les spectateurs à poser des questions dans le forum.

Révisions Maths lycée

Analyse Terminale

ECG

Dériver une composée

Dans cette vidéo, nous allons apprendre comment dériver une fonction composée. La composition de fonctions a été étudiée en détail, avec des contraintes sur les ensembles d'arrivée et de départ des fonctions. Pour dériver une fonction composée, nous allons utiliser des exemples simples que nous connaissons déjà. Pour une fonction dérivable u et un réel x, on peut dire que la dérivée de 1/x est -1/x^2. De la même manière, la dérivée de 1/u est -u'/u^2. Il est important de ne pas oublier la dérivée de u dans cette formule. En reprenant l'exemple de la racine carrée de x, la dérivée de la racine carrée de u est u'/2√u, encore une fois en n'oubliant pas la dérivée de u. La généralité qui se dégage de ces exemples est que la dérivée d'une fonction composée est égale à la dérivée de la fonction de départ appliquée à la fonction d'arrivée, multipliée par la dérivée de la fonction d'arrivée. Il faut toujours se rappeler de multiplier par la dérivée de la fonction d'arrivée. La définition formelle de la dérivée d'une fonction composée est que si u et v sont deux fonctions dérivables, la dérivée de v composée avec u est égale à la dérivée de v appliquée à u, multipliée par la dérivée de u. Une conséquence importante de cela est que si les fonctions v et u ont la même monotonie (croissante ou décroissante), alors la fonction composée v composée avec u est également croissante. Par contre, si les fonctions ont des monotonies opposées, la fonction composée sera décroissante. Pour résumer, pour dériver une fonction composée, on applique la dérivée de la fonction de départ à la fonction d'arrivée, en n'oubliant pas de multiplier par la dérivée de la fonction d'arrivée. Si les fonctions sont de même monotonie, la fonction composée sera croissante, sinon elle sera décroissante.

Révisions Maths lycée

Analyse Terminale

ECG

Fonction Composée

Ce cours explique comment effectuer l'étude et le tableau de variation d'une fonction composée de deux autres fonctions. L'exemple étudié est la fonction E2-1 sur x². La fonction composée est de la forme h rongé de x, où g est –1 sur x² et h est l'exponentielle. Par composition, f est défini sur R*. Pour faire le tableau de variation, les fonctions dérivées sont utilisées. g' est calculée et égale à 2 sur x³, ce qui est du même signe que x. Ainsi, g est décroissante de moins l'infini à 0 et croissante de 0 à plus l'infini. Les limites de g sont également calculées. En plus ou moins l'infini, g tend vers 0 et en 0, g tend vers moins l'infini. Toutes les limites sont ensuite utilisées pour construire le tableau de variation complet de g. La fonction est ensuite tracée pour observer son comportement. Il est également mentionné que si la fonction est paire, il est possible d'étudier uniquement une partie de la fonction sur un intervalle. Ensuite, le sens de variation de la fonction composée F (H rongé de G) est étudié. La fonction exponentielle H est croissante sur R et le sens de variation de G a déjà été déterminé. Ainsi, il est déduit que F est décroissante sur R étoile moins et croissante sur R étoile plus. Les limites de F sont calculées. En moins l'infini, G tend vers 0, et en composant avec H, F tend également vers 1. En 0, G tend vers moins l'infini, et en composant avec H, F tend vers 0. Le tableau de variation de F est ainsi obtenu, montrant qu'elle est décroissante de 1 à 0 et croissante de 0 à 1. Enfin, il est mentionné que la fonction n'est pas définie en 0, mais on peut prolonger la fonction par continuité en posant F de 0 égale à 0. Une autre méthode aurait pu être d'étudier directement la fonction F en calculant sa dérivée.