Cours de Géométrie avec Repères en Ligne par les Meilleurs Professeurs - Géométrie avec Repères

Point 1 : définition vecteur normal

This lesson is about finding the direction and normal vectors of a line, and then using them to determine the equation of a perpendicular line passing through a given point. The example in the lesson shows step-by-step how to find the direction vector of a line, as well as the equation of a perpendicular line passing through a given point. The lesson emphasizes the importance of making a quick sketch to better visualize the problem being solved. By following the fundamental definitions taught in this lesson, one can find equations for lines in a straightforward manner.

Trouver une droite à partir d'un vecteur normal

Dans ce cours, nous apprenons comment trouver l'équation d'une droite en connaissant un point et un vecteur normal. La première étape consiste à utiliser le vecteur normal pour trouver la forme générale de l'équation, qui est de la forme ax+by+c=0. Ensuite, nous utilisons le point donné pour calculer la constante c. En résolvant cette équation, nous pouvons trouver l'équation finale de la droite. Dans cet exemple, la droite est représentée par moins 2x plus 4y plus 6 égale zéro, qui peut également être écrite sous forme simplifiée de moins x plus 2y moins 3 égale zéro.

Utiliser vecteur directeur ET vecteur normal

This lesson covers how to find both the direction and normal vectors of a given line, and then how to use them to calculate a new line perpendicular to the first passing through a given point. A vector "-b-a" can be used as a direction vector, with a being the coefficient before y. The normal vector can be found from the Cartesian equation of the line through "-b-a". To find the equation of a new line perpendicular to the first, a direction vector can be used as a normal vector for the new line. The equation can then be found by applying the standard formula, using a known point on the new line to solve for the constant. Finally, the reduced equation can be found by isolating for the y variable.

Trouver un projeté orthogonal

Ce cours explique comment trouver les coordonnées d'un projeté orthogonal en utilisant les vecteurs normaux. Il s'agit de trouver la distance la plus courte entre un point T et une droite en traçant une droite orthogonale, et ensuite trouver les coordonnées du point H. Pour cela, il faut trouver une équation de la droite HT avec un vecteur normal de la droite initiale. Ensuite, on résout un petit système pour trouver les coordonnées du point H en utilisant l'appartenance du point aux deux droites. Les coordonnées du point H sont alors 45 treizième et moins 30 treizième dans l'autre sens.

Point 2 : équation d'un cercle

Ce cours traite des cercles en géométrie repérée. Un cercle est défini comme l'ensemble des points à une distance fixe d'un point central. Ainsi, un point M appartient au cercle de centre O et de rayon R si et seulement si la distance entre O et M est égale à R. L'équation d'un cercle est alors exprimée comme (X-A)² + (Y-B)² = R². Le cours explique comment trouver l'équation cartésienne d'un cercle à partir de son centre et de son rayon, et donne un exemple. Il est important de retenir cette définition pour pouvoir appliquer la méthode dans des problèmes similaires.

Cercle défini par son diamètre

Cette vidéo montre comment trouver l'équation d'un cercle en utilisant son diamètre plutôt que son centre et son rayon. Tout d'abord, il faut trouver le centre en utilisant la formule pour le milieu d'un segment. Ensuite, la longueur du segment est divisée par deux pour obtenir le rayon. Enfin, en appliquant la formule de l'équation d'un cercle, on peut trouver l'équation du cercle de diamètre AB.

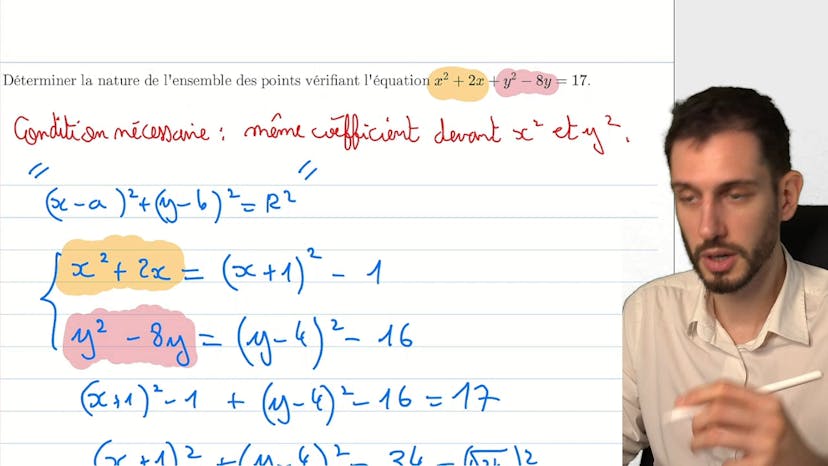
CAPITAL : savoir reconnaître et factoriser l'équation d'un cercle

La méthode du cercle consiste à partir d'une équation développée pour retrouver un cercle. Pour cela, il est nécessaire d'avoir le même coefficient devant x² et y². Si c'est le cas, on utilise l'identité remarquable pour obtenir une forme canonique. On résout ensuite pour obtenir l'équation du cercle et les coordonnées de son centre et de son rayon. Cependant, avoir le même coefficient n'est pas une condition suffisante pour avoir un cercle, parfois c'est un point. Donc il faut être vigilant. En résumé, pour trouver le cercle à partir d'une équation complexe, il faut rechercher le même coefficient devant x² et y², puis utiliser l'identité remarquable et la forme canonique pour retrouver l'équation du cercle.

Cercle : équation à coéfficients non usuels

Dans cet exercice, l'équation développée contient des termes en x² et y², mais avec des coefficients différents. Cependant, comme les coefficients devant x² et y² sont les mêmes, il est possible que ce soit un cercle. En divisant par 3, on obtient une forme qui permet d'appliquer la méthode de la forme canonique. On peut ainsi exprimer l'équation sous la forme (x-1)² + (y+1/3)² = 13/9, ce qui correspond à un cercle de centre (1,-1/3) et de rayon racine de 13/3. L'exercice démontre ainsi que des coefficients différents devant x² et y² ne sont pas un obstacle pour résoudre une équation du second degré.

Déterminer la tangente à un cercle

Dans cet exercice, on étudie le concept de tangente par rapport à un cercle. Une tangente est une droite qui touche un cercle en un seul point et est perpendiculaire au rayon qui passe par ce point. On commence par trouver l'équation cartésienne d'un cercle donné et vérifier qu'un point donné appartient bien à ce cercle. Ensuite, on cherche à trouver l'équation de la tangente qui passe par ce point. On utilise le vecteur normal, qui est le vecteur orthogonale à la tangente, et les coordonnées de ce point pour trouver l'équation de la tangente. Dans cet exercice, on trouve que la tangente est une droite verticale, y égal 3. On peut utiliser ces concepts en géométrie pour résoudre différents problèmes.

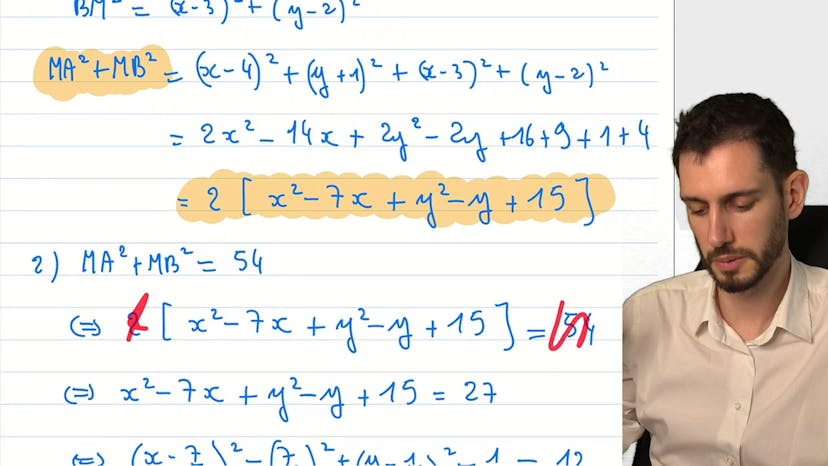
Trouver un ensemble de points particuliers

Ce cours porte sur la résolution d'un exercice de mathématiques consistant à trouver l'ensemble de points répondant à une équation donnée. On commence par exprimer l'équation sous la forme m a² + m b² + a54 en utilisant les points donnés dans l'énoncé. On simplifie ensuite l'équation en regroupant les termes, puis on factorise par le coefficient commun pour obtenir une équation de cercle. Ensuite, on utilise la technique de la forme canonique pour trouver l'équation de cercle compacte de l'ensemble de points. Il s'agit donc d'un exercice simple mais qui peut être présenté sous différentes formes, ce qui nécessite l'application des connaissances acquises précédemment.

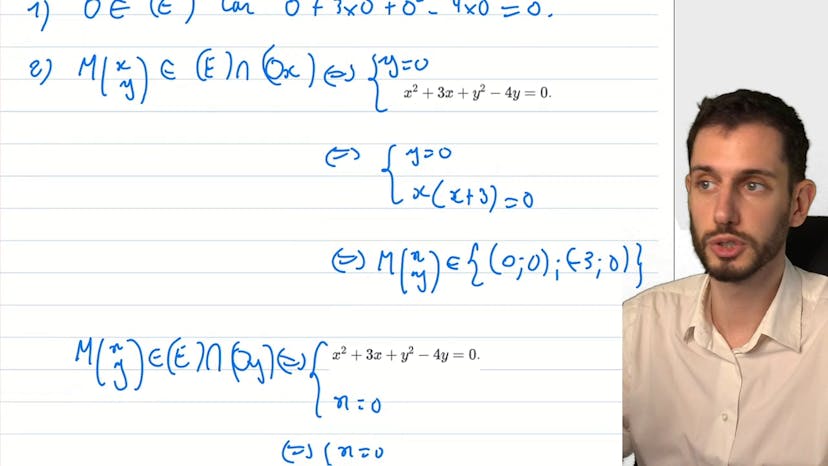
Cercle et intersections avec les axes

Dans cet exercice, nous étudions l'intersection d'un cercle avec certaines droites. Nous vérifions que l'ensemble passe par l'origine, déterminons les points d'intersection avec les deux axes du repère, montrons que l'ensemble est un cercle, déterminons son centre et son rayon. Nous utilisons la méthode de forme canonique pour obtenir l'équation factorisée du cercle. Ensuite, nous trouvons le centre en prenant les coordonnées du cercle, moins 3 demi pour X et 2 pour Y et le rayon est 5 demi.

Retrouver le centre d'un cercle circonscrit

Cet exercice porte sur l'étude du cercle circonscrit d'un triangle et demande de déterminer une équation cartésienne pour les médiatrices AB et AC, ainsi que les coordonnées du point O, le centre du cercle. Pour cela, on utilise les définitions de collège et les vecteurs normaux pour les médiatrices, puis résoudre un système d'équations pour trouver les coordonnées de O. Ensuite, on calcule la longueur OA et utilise cette valeur pour définir une équation cartésienne pour un cercle de rayon OA et de centre O. En vérifiant que ce cercle passe bien par les points B et C, on démontre que O est le centre du cercle circonscrit. Bien que l'exercice demande des calculs et des méthodes, cela peut être facilement maîtrisé en ayant une bonne compréhension des leçons précédentes.

Des cercles sécants !

Dans cet exercice, on utilise les cercles pour calculer les distances et la nature du triangle. Le cercle de centre A a un rayon de 3 et le cercle de centre B un rayon de 4. La première question consiste à calculer la distance AB, qui est de 5, pour montrer que les deux cercles sont séquents. La deuxième question demande de donner les équations cartésiennes, qui sont simplement appliquées à partir des données du cercle. La troisième question demande de montrer que le point C appartient aux deux cercles, ce qui est vérifié en remplaçant les coordonnées de C dans les équations. Enfin, la quatrième question demande de déduire la nature du triangle ABC. En utilisant la relation de Pythagore, on montre que le triangle est rectangle et de mesure 3-4-5. Il est important de comprendre les questions et l'exercice dans son ensemble pour réussir.

Un paramètre dans une équation de cercle

Le cours traite de la résolution d'une équation qui pourrait potentiellement avoir une forme de cercles. Après avoir étudié les termes impliquant x, l'équation peut être réécrite sous la forme d'un cercle si la quantité a² - 4 est positive stricte. Dans le cas où a² - 4 est égal à zéro, deux points de solution sont trouvés, et s'il est négatif, alors l'ensemble des solutions est vide. En résumé, la solution pour a est un cercle si a est plus grand que 2 ou plus petit que -2, deux points si a est égal à 2 ou -2, et l'ensemble vide pour tout le reste. La clé pour résoudre l'équation est d'appliquer la méthode appropriée, de discuter de la positivité ou de la négativité du rayon, et d'examiner l'existence ou non d'une solution.