Cours de Mécanique en Ligne par les Meilleurs Professeurs - Mécanique

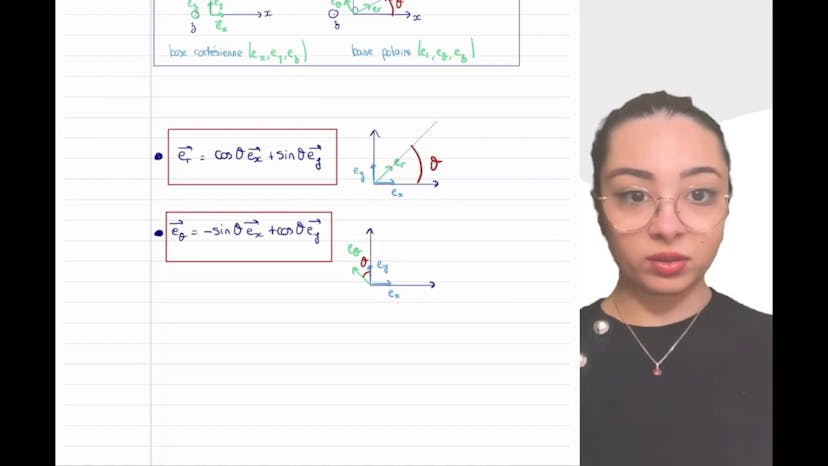
Base cylindrique

Dans ce cours, Layla explique l'importance de savoir projeter des vecteurs d'une base à une autre en mécanique. Pour ce faire, elle explique les bases cylindrique et cartésienne, puis donne les formules pour exprimer les vecteurs de la base cylindrique en fonction de ceux de la base cartésienne. Elle conseille de zoomer sur la partie de la projection pour avoir une meilleure compréhension. Enfin, Layla invite les étudiants à poser leurs questions en commentaire.

Vitesse et accélération

Dans ce cours, Leïla explique comment exprimer la vitesse et l'accélération d'un point en coordonnées cylindriques. Elle utilise la formule OM = RER + ZEZ pour déterminer le vecteur déplacement. Elle note que ER change en fonction de la base, mais EZ est fixe. Elle mentionne également la formule DER/Dt = θ.eθ et DET/Dt = -θ.er pour dériver les vecteurs mobiles par rapport au temps. Pour la vitesse, elle dérive le vecteur position par rapport au temps et applique la formule DER/Dt = θ.eθ pour obtenir l'expression de la vitesse en coordonnées cylindriques R.ERθ.ez. Pour l'accélération, elle dérive la vitesse et applique la formule des produits de trois termes pour obtenir l'expression de l'accélération en coordonnées cylindriques. Elle insiste sur l'importance de connaître cette formule pour résoudre les problèmes de mécanique en base cylindrique.

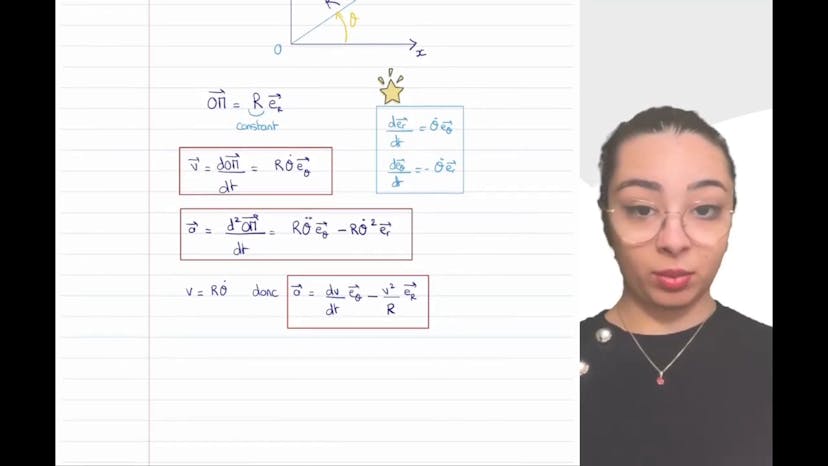
Mouvement circulaire

Dans cette vidéo, Leïla décompose le mouvement circulaire en coordonnées polaires, avec les vecteurs ER et Eθ. Elle rappelle l'importance de se souvenir de l'encadré de la dérivée des vecteurs de la base mobile pour manipuler des mouvements circulaires ou des coordonnées cylindriques. Pour exprimer la vitesse et l'accélération d'un point M, elle utilise la formule V = Rθ pour la vitesse et A = DV/DT Eθ - V²/R ER pour l'accélération, en accédant directement à la vitesse en norme.

Course-poursuite

Le sujet de cet exercice de cinématique est la loi horaire. Un conducteur roule à une vitesse constante sur une route rectiligne. Un gendarme qui démarre à l'instant où la voiture passe à sa hauteur accélère uniformément. Les lois horaires sont utilisées pour déterminer le temps nécessaire au gendarme pour rattraper la voiture, la distance parcourue et la vitesse atteinte. Pour le conducteur, la vitesse est constante à 100 km/h, donc sa position est donnée par Xc(t) = V0t. Pour le gendarme, son accélération est constante A0, donc sa vitesse est donnée par Vg(t) = A0t et sa position est calculée par Xg(t) = 0.5*A0t². En utilisant ces lois horaires, on peut déterminer que le gendarme rattrape la voiture en 22 secondes, parcourt une distance de 617 mètres et atteint une vitesse de 55,5 m/s.

Accélération et décélération

Dans ce cours de cinématique, Leïla nous explique comment mesurer l'accélération et la décélération d'une voiture en utilisant un test d'accélération chronométré en ligne droite, et comment appliquer ces concepts en sport automobile. Elle nous donne un exemple de calcul d'accélération en utilisant la distance parcourue et le temps chronométré, puis un exemple de calcul de distance d'arrêt en utilisant une décélération donnée. Elle explique la modélisation nécessaire pour prendre en compte les changements d'accélération et les nouvelles origines des temps. En utilisant les lois horaires de la vitesse, de l'accélération et de la position, elle montre comment calculer la vitesse atteinte à une distance donnée et la distance d'arrêt pour une décélération donnée.

Ballon Sonde

Dans cet exercice, nous modélisons un ballon sonde par un point matériel avec pour coordonnées x de t et z de t. Le ballon est lâché depuis le point 0 à l'instant t=0 et a une vitesse verticale constante de v0 tout au long de son mouvement. En plus, une vitesse horizontale vx, positive et proportionnelle à son altitude, est transmise par le vent. Z de t vérifie une équation différentielle simple, z point est égale à v0. Nous résolvons cette équation différentielle pour obtenir z de t égal à v0 t. Nous obtenons l'expression de vx en fonction de z qui nous permet d'calculer x de t. Ensuite, nous obtenons l'équation de la trajectoire du ballon, z en fonction de x, qui est en forme de racine. Nous suggérons de tracer les z points de la courbe et d'interpréter les informations sur la vitesse et l'accélération. L'accélération est nulle selon z et v0 sur taux selon x. N'oubliez pas de bien faire attention à l'orientation des vecteurs.

Hélice circulaire

Le cours concerne l'exercice pratique sur l'hélice circulaire où un point matériel suit un mouvement dans une direction de coordonnées cylindriques constantes. Le module de la vitesse est constant et il est calculé en prenant la racine carrée de ce qui se passe selon θ au carré et selon Z au carré, et il est indépendant du temps. Toutefois, le mouvement peut changer de direction avec Eθ, donc la vitesse n'est pas constante. L'accélération est obtenue en dérivant la vitesse par rapport au temps et en prenant en compte les coordonnées cylindriques. L'exercice a été résolu en utilisant les lois horaires et les vecteurs ER et Eθ.

La Guerre des étoiles

Dans cet exercice de physique sur la cinématique, un véhicule suit une trajectoire sinusoidale entre des cheminées d'une usine. La vitesse du véhicule est constante selon x et il met 12 secondes pour revenir sur l'axe après la sixième cheminée. L'amplitude de la sinusoïde doit être déterminée pour que l'accélération reste inférieure à 10G en valeur absolue. Pour modéliser le mouvement sinusoidal, l'utilisation d'un sinus ou d'un cosinus est avantageuse en fonction du point de départ. La période du sinus est de 2 pi et la hauteur est donnée par la formule Y0 sinus de pi X sur L. En isolant le temps dans l'équation de trajectoire et en dérivant une fois et deux fois, l'accélération selon y peut être calculée. Pour limiter l'accélération en dessous de 10G, l'amplitude de la sinusoïde doit être inférieure à 40 mètres. L'exercice montre également comment convertir les mètres par seconde en kilomètres par heure.

Mouvement sur une ellipse

Dans ce cours, on apprend à calculer le mouvement d'un point M qui se déplace sur une ellipse. On utilise l'équation cartésienne de l'ellipse pour déterminer les coordonnées du point M à différents moments. On montre également comment déduire la valeur de bêta en utilisant l'équation de l'ellipse. On calcule ensuite la vitesse et l'accélération du point en dérivant les équations horaires de M. Finalement, on montre que l'accélération a est de la forme -oméga carré om, qui correspond à un mouvement d'oscillateur harmonique. On souligne l'importance de connaître les ellipses en physique et en mécanique, car elles apparaissent souvent dans l'étude des mouvements planétaires.

Pendule

Le cours parle du pendule simple en physique, où un point est attaché à un fil de longueur L fixé à un point O. Le mouvement est enregistré en coordonnées polaires, et on observe des oscillations pendulaires. Les vecteurs position, vitesse et accélération sont ensuite déterminés en utilisant des coordonnées polaires et cartésiennes, en changeant l'origine du repère. Il est important de connaître les dérivées des vecteurs de base pour résoudre les problèmes et manipuler les différents repères. Les oscillateurs harmoniques sont souvent observés dans les mouvements décrits.

Chute libre

Dans ce cours, Leïla explique comment calculer l'équation de la trajectoire pour une chute libre sans frottement. Elle rappelle que la caractéristique principale de la chute libre est l'absence de force autre que la pesanteur. Elle utilise des équations mathématiques pour exprimer la vitesse et la position de l'objet en fonction du temps, puis elle isole le temps pour obtenir l'équation de la trajectoire en fonction de la position. Elle souligne que la maîtrise de ces équations est importante pour résoudre des problèmes plus complexes liés à la chute libre. Elle invite les spectateurs à poser des questions en commentaire.