Cours de Fonctions : convexité (3) en Ligne par les Meilleurs Professeurs - Fonctions : convexité (3)

Des inégalités classiques

Dans cet exercice, on étudie différentes inégalités en utilisant les concepts de convexité et de concavité. La première inégalité à démontrer est que pour tout réel X, l'exponentiel de X est supérieur à 1+X, même si X est non nul. On commence par chercher un lien entre l'exponentiel de X et 1+X. On remarque que 1+X peut s'écrire comme l'exponentiel de 0 fois X moins 0 plus l'exponentiel de 0. On reconnaît ainsi l'équation de la tangente à la courbe de l'exponentiel de X au point d'abscisse X=0 et d'ordonnée 1. En étudiant la convexité de la fonction exponentielle, on montre que la courbe de cette fonction est strictement au-dessus de cette tangente, en dehors du point de contact. On en déduit que pour tout X réel, l'exponentiel de X est supérieur ou égal à 1+X, avec égalité seulement en X=0. Ensuite, on souhaite montrer que le logarithme de 1+X est inférieur ou égal à X. En étudiant la convexité de la fonction logarithme de 1+X, on montre qu'elle est strictement concave. On en déduit que la courbe de cette fonction est strictement en-dessous de sa tangente en X=0. On écrit donc l'équation de cette tangente et on l'utilise pour montrer que le logarithme de 1+X est inférieur ou égal à X, avec égalité en X=0. Finalement, on souhaite encadrer la fonction sinus de X entre pi/2 et X pour X dans l'intervalle [0, pi/2]. On étudie la convexité de la fonction sinus et montrons qu'elle est concave sur cet intervalle. On utilise ensuite une tangente en X=0 pour montrer que la fonction sinus de X est inférieure ou égale à X. Enfin, on utilise une corde entre les points (0, pi/2) et (pi/2, 1) pour montrer que la fonction sinus de X est supérieure ou égale à pi/2. On conclut donc que la fonction sinus de X est bien encadrée entre pi/2 et X pour X dans l'intervalle [0, pi/2].

Inégalité de Bernoulli

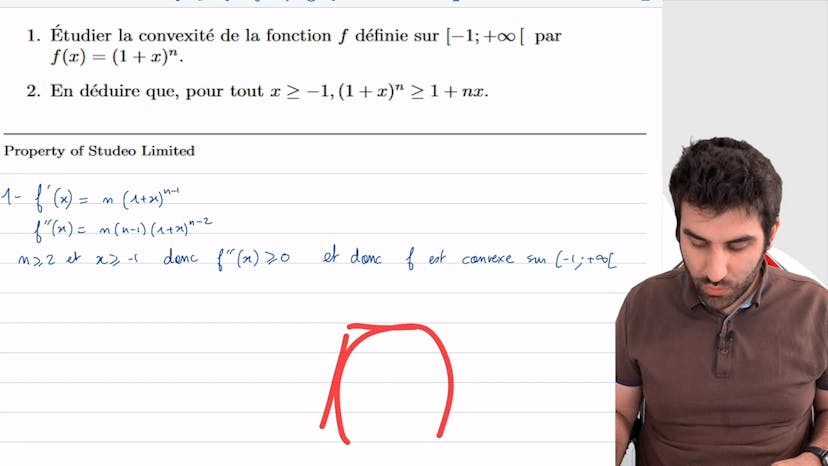
Dans cet exercice, nous montrons l'inégalité de Bernoulli en utilisant la convexité de la fonction 1+x^n. Habituellement, cette inégalité est démontrée en utilisant le raisonnement par récurrence, mais ici nous utilisons la convexité. Pour étudier la convexité de la fonction sur l'intervalle (-1, +∞), nous dérivons deux fois la fonction et étudions le signe de la dérivée. La dérivée première est n(1+x^(n-1)) et la dérivée seconde est n(n-1)(1+x^(n-2)). Comme n>2 et x>-1, les dérivées sont positives. Ainsi, f' est positive et donc f est convexe sur (-1, +∞). Nous en déduisons alors que pour x>-1, 1+x^n > 1+nx, ce qui est l'inégalité de Bernoulli. Une propriété importante à retenir est qu'une fonction convexe est toujours au-dessus de ses tangentes. Donc, pour obtenir une inégalité avec une fonction affine, il suffit de considérer la fonction affine comme une tangente de la fonction convexe. En utilisant cette propriété, nous considérons la fonction 1+x^n comme une tangente de f au point d'abscisse 0. En vérifiant que 1+nx est bien l'équation de cette tangente, nous concluons que f(x) est plus grand que 1+nx. Ainsi, 1+x^n > 1+nx sur l'intervalle (-1, +∞).

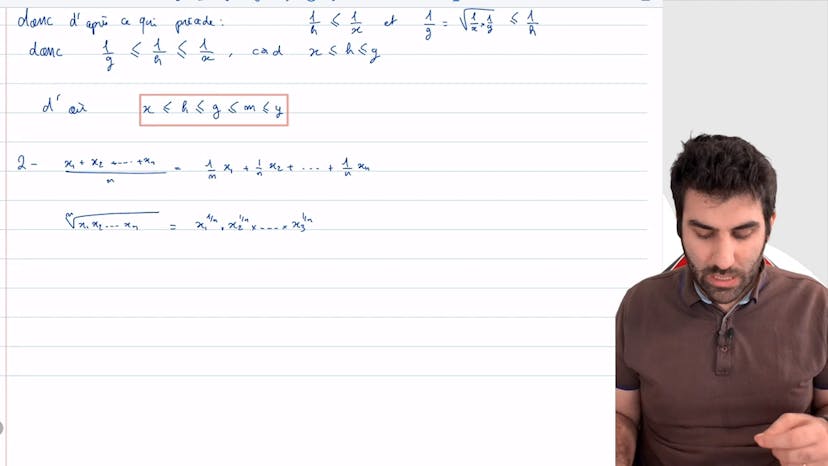
Moyennes arithmétique et géométrique

Dans cet exercice, on nous donne les définitions des moyennes arithmétique, géométrique et harmonique. Nous devons montrer que la moyenne géométrique est plus petite que la moyenne arithmétique, et que cette dernière est plus petite que la moyenne harmonique. Pour prouver cela, nous commençons par montrer que la moyenne arithmétique est plus petite que le plus grand des deux nombres. Ensuite, nous démontrons que la moyenne géométrique est plus petite que la moyenne arithmétique. Enfin, nous montrons que la moyenne harmonique est plus grande que le plus petit des deux nombres. Ensuite, nous démontrons que la moyenne géométrique est plus grande que le plus petit des deux nombres. En utilisant les inverses des nombres, nous montrons également que la moyenne harmonique est plus grande que la moyenne géométrique. Nous utilisons ensuite ces résultats pour montrer que la moyenne harmonique est entre le plus petit et le plus grand des deux nombres. Finalement, nous démontrons le cas général pour une moyenne géométrique et une moyenne arithmétique avec plus de deux nombres. Nous utilisons la convexité de la fonction logarithme pour montrer que la moyenne géométrique est plus petite que la moyenne arithmétique. En résumé, nous avons démontré que la moyenne géométrique est plus petite que la moyenne arithmétique, elle-même plus petite que la moyenne harmonique. Cette démonstration s'appuie sur les relations entre les différentes moyennes et utilise la convexité de la fonction logarithme.

Points d’inflexion

Dans cet exercice, nous allons étudier une fonction pour déterminer ses points d'inflexion. Une fonction admet un point d'inflexion en x0 si et seulement si la dérivée seconde f'' change de signe en x0. Nous allons donc calculer la dérivée seconde de la fonction. On obtient ainsi : f'' = -cos(3x) * cos(x) - cos(2x). Pour étudier le signe de cette expression, il est préférable de factoriser. En utilisant une formule trigonométrique (cos(a) + cos(b) = 2cos((a+b)/2)*cos((a-b)/2)), on peut factoriser f'' en -cos(2x) * (2cos(2x) + 1). Maintenant que f'' est factorisée, on peut étudier le signe de chaque facteur. Pour que -cos(2x) soit positif, cos(2x) doit être négatif, c'est-à-dire quand x est entre pi/4 et 3pi/4. Pour que 2cos(2x) + 1 soit positif, cos(2x) doit être supérieur ou égal à -1/2, c'est-à-dire quand x est entre 0 et 2pi/3 ou entre 7pi/3 et 2pi. En résumé, les points d'inflexion de la fonction sont de la forme pi/4 + kpi/2 en abscisse et f(pi/4 + kpi/2) en ordonnée, avec k appartenant à Z, ainsi que 2pi/3 + 2kpi et -2pi/3 + 2kpi en abscisse et f(2pi/3 + 2kpi) et f(-2pi/3 + 2kpi) en ordonnée, avec k appartenant à Z.

Majoration de f ’ grâce à f ”

Dans cet exercice, nous devons majorer une fonction de classe C2 par une autre fonction dépendant de M, le sup de la dérivée seconde sur AB. Pour justifier l'existence de M, nous utilisons l'hypothèse que F est de classe C2, ce qui signifie que la dérivée seconde est continue sur AB. Étant donné que la fonction est continue sur un segment, elle est bornée et atteint ses bornes. Par conséquent, le sup existe. On nous présente ensuite les fonctions G et H et on nous demande de montrer que G est convexe et H est concave. Pour cela, nous calculons les dérivées secondes de G et H et en étudions le signe. En utilisant la convexité de G et la concavité de H, nous déduisons une inégalité impliquant la valeur absolue de la dérivée de F. Enfin, nous regroupons les éléments pour obtenir l'inégalité finale de la valeur absolue de F.

Inégalité de Hölder et Minkowski

Aucun résumé n'est disponible pour cette vidéo

Fonctions convexes avec asymptote

Dans cet exercice, on utilise l'inégalité des pentes pour montrer certains résultats liés à une fonction convexe. Tout d'abord, on suppose que la limite de la fonction, lorsque x tend vers l'infini, est égale à zéro, et on doit montrer que la fonction est positive. On raisonne par l'absurde en supposant qu'il existe un x0 pour lequel la fonction est strictement négative. En utilisant la définition de la limite, on peut trouver un x1 plus grand que x0 tel que la fonction soit comprise entre f(x0) et zéro. Par l'inégalité des pentes, on montre que f(x) est strictement plus grand que cette expression. Cependant, cette expression est une fonction affine avec un coefficient directeur strictement positif, ce qui signifie qu'elle tend vers l'infini lorsque x tend vers l'infini. Cette contradiction montre que la fonction ne peut pas être négative, donc elle est positive pour tout x. Ensuite, on nous demande de montrer que la somme d'une fonction convexe et d'une fonction affine est convexe. Au lieu d'utiliser la dérivée seconde comme d'habitude, on utilise une approche différente, car on n'a pas d'information sur la dérivabilité de la fonction. On pose une fonction g qui est la somme de la fonction convexe f et de la fonction affine ax + b. On veut montrer l'inégalité de convexité, c'est-à-dire que g(tx + (1-t)y) est plus petit que t(g(2x) + (1-t)g(2y)), où t est un nombre entre 0 et 1. On remplace g par son expression et on réarrange les termes pour obtenir l'inégalité désirée. Enfin, on suppose que la courbe représentative de f a une asymptote et on doit montrer que la courbe est toujours au-dessus de cette asymptote. On pose y = x + b comme équation de l'asymptote. On définit g_2(x) comme f_2(x) - ax + b, qui est la différence entre la fonction et l'asymptote. En utilisant le fait que l'asymptote tend vers 0 lorsque x tend vers l'infini, on montre que la limite de g_2(x) est également 0. En utilisant les questions précédentes, où on a montré que g est convexe et positive, on en déduit que f_2(x) est toujours plus grand que ax + b, c'est-à-dire que la courbe de f est toujours au-dessus de son asymptote.