 Tous les sujets
Tous les sujets Maths
Maths Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée- Analyse Terminale
- Géométrie Terminale
- Probas Terminale
- Dénombrement
- Variables aléatoires
- Concentration et Loi des Grands Nombres
- Arithmétique Maths expertes
- Complexes Maths expertes
MPSI/PCSI Prépa Examens
Prépa Examens
Terminale
Première
Seconde
MPSI/PCSI
2BAC SM Maroc
 Tous les sujets
Tous les sujets Maths
Maths Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée- Analyse Terminale
- Géométrie Terminale
- Probas Terminale
- Dénombrement
- Variables aléatoires
- Concentration et Loi des Grands Nombres
- Arithmétique Maths expertes
- Complexes Maths expertes
MPSI/PCSI Prépa Examens
Prépa Examens
Révisions Maths lycée
Probas Terminale
MPSI/PCSI

Principe multiplicatif
Dans cet exercice sur les échanges de poignées de mains entre deux équipes de 15 personnes, on cherche à déterminer le nombre de poignées de mains échangées. Pour résoudre ce problème, il faut analyser la notion de poignée de main en tant que lien entre deux personnes appartenant à des équipes différentes. On peut donc former une paire en choisissant une personne de l'équipe 1 et une personne de l'équipe 2. Il y a 15 possibilités dans l'équipe 1 et 12 possibilités dans l'équipe 2, ce qui donne un total de 180 poignées de mains possibles. Il est important de noter que chaque poignée de main est comptée une seule fois, car on a établi une liste où le premier élément vient de l'équipe 1 et le second élément vient de l'équipe 2. Ainsi, on évite de compter deux fois la même paire en inversant les rôles des équipes. En comprenant qu'il s'agit de compter des paires, le problème devient plus simple à résoudre.
Révisions Maths lycée
Probas Terminale
MPSI/PCSI

Cours par cas pratiques !
Lors de ce cours, nous traitons de la détermination du nombre d'anagrammes, c'est-à-dire le nombre de façons de combiner les lettres d'un mot. Pour calculer ce nombre, nous utilisons la notion de permutation, qui correspond au nombre de choix possibles pour ranger les lettres dans des cases. Par exemple, pour le mot ABC, il y a 3! (3 factorielle) façons de l'organiser, car il y a 3 lettres et 3 cases. De même, pour les mots CHA, CHIEN et VALISE, nous utilisons respectivement 3!, 4!, 5! et 6! pour déterminer leur nombre d'anagrammes.
Ensuite, nous abordons des mots avec des lettres répétées, comme AXA. Dans ce cas, nous devons prendre en compte le fait que les lettres identiques ne peuvent pas être distinguées. Par exemple, pour AXA, nous aurons seulement 3 choix possibles (AAX, AXA, XAA) au lieu de 6, car les deux lettres A peuvent être permutées entre elles. Ainsi, pour chaque combinaison de lettres, nous devons diviser par le nombre de permutations possibles des lettres identiques.
Nous généralisons ensuite ce raisonnement pour des mots plus complexes tels que "visir" et "abracadabra". Pour ces mots, nous prenons en compte le nombre de lettres répétées (par exemple, 2 a dans "abracadabra") et le nombre de permutations possibles pour chaque lettre. Nous calculons donc le nombre d'anagrammes en utilisant le nombre total de lettres et en divisant par le produit des facteurs correspondant aux lettres répétées.
En conclusion, le calcul du nombre d'anagrammes peut être complexe, mais en utilisant les principes de permutation et en prenant en compte les lettres répétées, nous pouvons obtenir des résultats précis. Cela nous permet de comprendre et de déterminer le nombre de combinaisons possibles pour des mots donnés.
Révisions Maths lycée
Probas Terminale
MPSI/PCSI

Déterminer des ensembles
Dans ce cours sur le dénombrement, on va traiter des ensembles et des listes. Un ensemble est comme un sac qui contient des objets, sans ordre spécifique. Une liste, en revanche, est une séquence d'objets avec un ordre précis. Les ensembles peuvent contenir d'autres ensembles, tandis que les listes représentent des coordonnées (ex: 1-2 n'est pas la même chose que 2-1). Lorsqu'on aborde des problèmes où l'ordre compte, on travaille avec des listes, sinon on utilise des ensembles et les combinatoires.
Dans l'exemple donné, on a deux ensembles E et F, avec des éléments en commun. L'union des deux ensembles (E U F) comprend tous les éléments de E et/ou F. L'intersection (E I F) regroupe les éléments communs à E et F. Le produit cartésien (E croix F) est une liste de couples formés d'un élément de E et d'un élément de F. Une paire est un ensemble de deux éléments.
La distinction entre ensembles et listes est essentielle pour comprendre les différentes méthodes de dénombrement. Si vous avez des questions, n'hésitez pas à les poser.
Révisions Maths lycée
Probas Terminale
MPSI/PCSI

Utiliser un diagramme
En utilisant les diagrammes, nous pouvons dénombrer les différentes catégories visuellement. Dans cet exemple, nous avons une station de sport d'hiver avec 20 touristes. Parmi eux, 14 pratiquent le ski de piste, 7 pratiquent le ski de fond, et 4 pratiquent les deux.
Pour représenter cela, nous pouvons dessiner un diagramme. Nous plaçons les 20 touristes à l'intérieur d'une bulle bleue. Parmi ces touristes, 10 pratiquent uniquement le ski de piste, 4 pratiquent à la fois le ski de piste et le ski de fond, et 3 pratiquent uniquement le ski de fond.
Pour trouver combien de touristes ne pratiquent aucune de ces activités, nous comptons simplement : 10 + 4 + 3 = 17. Donc, sur les 20 touristes initiaux, il y en a 3 qui ne pratiquent rien du tout.
Même si cet exemple est simple, le principe reste le même pour des diagrammes plus complexes.
Révisions Maths lycée
Probas Terminale
MPSI/PCSI

Dénombrer des ensembles simples
Le cours aborde le dénombrement et illustre des exemples. Dans le premier exemple, on lance une pièce pile ou face 7 fois de suite. On détermine le nombre de résultats possibles en considérant que c'est une liste où l'ordre compte et où on peut répéter plusieurs fois le même résultat. Ainsi, le nombre de tirages possibles est de 2 à chaque fois, soit 2 à la puissance 7.
Dans le deuxième exemple, deux joueurs reçoivent 7 dominos au hasard parmi les 28 du jeu. On cherche à déterminer le nombre de distributions possibles en considérant que c'est une liste où l'ordre compte. Il n'y a pas de répétition possible, donc on dénombre en partant de 28 pour le premier tirage et en diminuant de 1 à chaque tirage, pour un total de 2 fois 7 dominos. On utilise une astuce pour déterminer la limite de tirage. On exprime également le résultat sous forme factorielle.
Dans le dernier exemple, il y a 4 gâteaux et 4 invités. Chaque invité doit recevoir un gâteau. On considère que c'est une liste où l'ordre compte et où il n'y a pas de répétition possible. Ainsi, on dénombre 4 factorial, c'est-à-dire 4 fois 3 fois 2 fois 1.
En conclusion, lorsqu'on effectue un dénombrement, il faut se poser deux questions : est-ce que l'ordre compte et est-ce qu'il peut y avoir des répétitions. Il est également recommandé de consulter la FAQ en cas de questions supplémentaires.
Révisions Maths lycée
Probas Terminale
MPSI/PCSI

Tirage successif sans remise
Dans ce cours, nous abordons la façon de compter des tirages successifs sans remise. Nous considérons un exemple où 5 élèves se tiennent en rang et nous voulons savoir combien de façons il y a de les ranger. Pour déterminer cela, nous devons tout d'abord répondre à quelques questions. S'agit-il d'une liste ou d'un ensemble ? Dans ce cas, il s'agit d'une liste car l'ordre compte. Y a-t-il une répétition ? Non, car nous ne pouvons pas avoir deux fois le même élève.
Maintenant que nous avons clarifié ces points, nous pouvons procéder au calcul. En première position, nous avons 5 choix possibles car nous pouvons choisir n'importe lequel des 5 élèves. En deuxième position, une fois que nous avons placé un élève, nous n'avons plus que 4 choix possibles, puis 3, puis 2, puis 1. Donc, en utilisant la formule générale, nous multiplions 5 par 4 par 3 par 2 par 1, ce qui équivaut à 5! (factorielle de 5).
Cette formule, N! sur N-P!, s'applique lorsque nous avons P tirages successifs sans remise dans un ensemble de N éléments. Pensez à retenir cette formule.
En résumé, pour les tirages successifs sans remise, nous utilisons la formule N! sur N-P!. Cela implique de choisir P éléments dans un ensemble de N éléments.
Révisions Maths lycée
Probas Terminale
MPSI/PCSI

Tirage successif avec remise
Le problème étudié concerne les échanges de poignées de mains entre deux équipes de 15 personnes chacune. Pour déterminer le nombre de poignées de mains, il est nécessaire de comprendre que chaque poignée de main correspond à une paire de personnes, une de chaque équipe. En utilisant cette notion de paire, on peut calculer le nombre de possibilités en multipliant le nombre de personnes dans chaque équipe (15 pour l'équipe 1 et 12 pour l'équipe 2), ce qui donne 180 poignées de mains au total. Il est également important de noter qu'il n'y a pas de doublons compte tenu de l'ordre des membres des équipes dans la liste des paires. Une fois cette compréhension établie, il devient plus facile de résoudre le problème.
Révisions Maths lycée
Probas Terminale
MPSI/PCSI
Principe multiplicatif et arbre pondéré
Dans ce cours, nous allons apprendre à faire un arbre pondéré, qui est utile pour dénombrer les différentes possibilités. Cependant, il faut noter que cela prend du temps à faire, donc il faut évaluer si cela vaut la peine de le faire en fonction du nombre de sous-branches. Au début, il est toujours bon de le faire au brouillon pour avoir des idées claires.
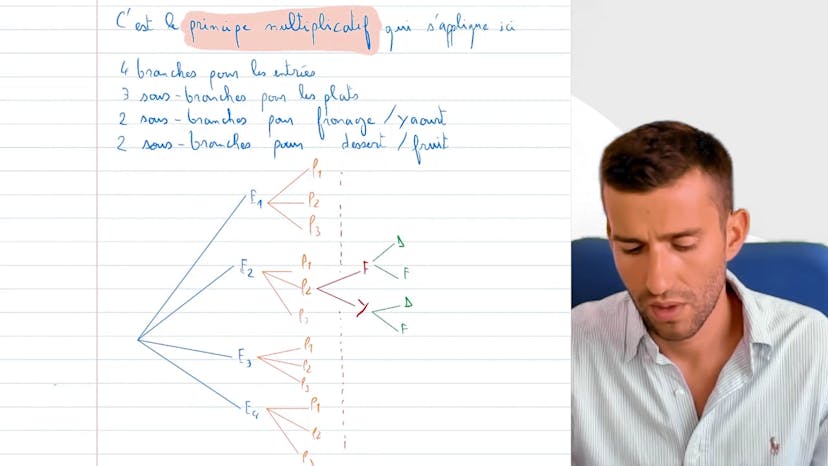
L'exemple utilisé est celui d'une cantine scolaire proposant des menus différents aux élèves. Chaque élève peut choisir entre 4 entrées, 3 plats, puis entre fromage ou yaourt, et dessert ou fruit. Nous devons trouver combien de menus possibles peuvent être constitués.
Pour construire l'arbre pondéré, nous commençons par les 4 entrées, puis pour chaque entrée, nous ajoutons les 3 plats possibles. Ensuite, nous avons le choix entre fromage et yaourt, et entre dessert ou fruit. Cependant, dans l'exemple donné, nous n'allons pas tout explorer, car cela ferait trop de branches.
Pour compter les possibilités, nous utilisons le principe multiplicatif. Donc, nous multiplions chaque possibilité : 4x3x2x2, ce qui donne 48 menus possibles.
Il est important de noter que cet arbre n'est pas pondéré. Les pondérations seraient utilisées pour les probabilités, lorsque certaines options ont des chances différentes d'être sélectionnées. Cependant, cela ne s'applique pas à ce stade, car nous sommes simplement en train de compter les possibilités.
Dans le prochain chapitre, nous aborderons les probabilités et la question de la pondération.
Révisions Maths lycée
Probas Terminale
MPSI/PCSI

Exo type en une minute !
Le cours présente un petit exercice où un candidat doit répondre à quatre questions indépendantes par vrai ou faux. Si le candidat répond au hasard, il y a 2 choix possibles pour chaque question, ce qui donne un total de 16 choix possibles. Ainsi, la probabilité d'obtenir les quatre bonnes réponses est de 1 sur 16. Cette exercice démontre simplement la randomité des réponses lors d'un test de ce type.
Révisions Maths lycée
Probas Terminale
MPSI/PCSI

Cours par la pratique 1
Aucun résumé n'est disponible pour cette vidéo
Révisions Maths lycée
Probas Terminale
MPSI/PCSI

Avec et sans ordre de tirage
Le cours porte sur la détermination du nombre de mains de 5 cartes dans un jeu de 32 cartes avec différentes combinaisons.
Tout d'abord, il est expliqué que le carré d'As fixe 4 des 5 cartes. Sachant qu'il y a 28 autres cartes dans le jeu, il est précisé que cette combinaison est très rare.
Ensuite, il est intéressant de déterminer le nombre de mains de 5 cartes de la même couleur dans un jeu de 32 cartes. On explique que pour cela, il est nécessaire de sélectionner 5 cartes parmi les 8 de la même couleur. Puisqu'il y a 4 couleurs dans un jeu de 32 cartes, le nombre total de mains possibles avec cette combinaison est donc de 4 fois le nombre de façons de sélectionner 5 cartes parmi 8.
Le cours continue en abordant la détermination du nombre de mains avec exactement une paire de cartes. Il est souligné que cette condition signifie qu'il ne doit pas y avoir deux paires ni un brelan. Pour résoudre ce cas, il est expliqué qu'il faut sélectionner les 3 cartes restantes une par une, en faisant attention à ne pas les prendre parmi les cartes de la paire déjà fixée. Ainsi, on obtient le nombre de mains possibles en multipliant le nombre de façons de sélectionner chaque carte parmi les cartes restantes.
Ensuite, on explique que pour chaque hauteur possible (7, 8, 9, 10, Valet, Dame, Roi, As), le nombre de paires possibles est de 2 parmi les 4 cartes de cette hauteur. Ainsi, le nombre total de mains possibles avec une paire donnée est obtenu en multipliant le nombre de façons de sélectionner une paire parmi les hauteurs possibles.
En résumé, le nombre total de mains possibles avec exactement une paire est obtenu en effectuant ces calculs pour chaque paire possible, c'est-à-dire pour chacune des 8 hauteurs possibles.
Révisions Maths lycée
Probas Terminale
MPSI/PCSI

Permutations : application
Dans ce cours, nous apprenons comment gérer les permutations. Une permutation se produit lorsque nous avons un ensemble ou une liste et que nous voulons savoir combien de façons il y a de changer l'ordre de cet ensemble. Par exemple, dans le cas d'un tirage de loto, nous voulons savoir combien de façons il y a de changer l'ordre du tirage une fois qu'il est fixé.
Dans cet exemple, nous avons une conférence avec 12 scientifiques, 6 hommes et 6 femmes, dont 5 mathématiciens, 3 physiciens et 4 biologistes. Chaque groupe de scientifiques a une méthode de placement différente.
La méthode des mathématiciens consiste à se placer au hasard, ce qui signifie qu'il y a 12 personnes déjà fixées et nous voulons savoir combien de façons il y a de les positionner. Le nombre de permutations pour un ensemble de n éléments est donné par la formule n!. Dans ce cas, nous avons 12 scientifiques, ce qui donne 12! permutations, soit 479 millions de possibilités.
La méthode des physiciens consiste à rester ensemble, ce qui signifie que les physiciens restent côte à côte et les autres sont répartis de manière aléatoire. Dans ce cas, nous avons déjà 10 positions possibles pour le premier physicien, puisqu'ils doivent rester ensemble. Ensuite, il y a 6 permutations possibles pour les deux autres physiciens. Enfin, les autres scientifiques peuvent être positionnés de n'importe quelle façon parmi les 9 places restantes. En utilisant le principe multiplicatif, nous avons 10 x 6 x 9 permutations possibles, soit 21 millions de possibilités.
La méthode des biologistes consiste à regrouper les hommes et les femmes ensemble. Dans ce cas, il y a 2 façons de positionner les deux groupes. Ensuite, chaque groupe peut être réparti de différentes façons, avec 6 permutations possibles pour les femmes et 6 permutations possibles pour les hommes. En utilisant le principe multiplicatif, nous obtenons 2 x 6! x 6!, soit 1 million 36 800 possibilités.
Nous utilisons le principe multiplicatif pour calculer le nombre de permutations dans ces exemples. Si vous avez des questions, n'hésitez pas à consulter la FAQ.


