Cours de Dénombrement en Ligne par les Meilleurs Professeurs - Dénombrement

Déterminer des ensembles

Dans ce cours sur le dénombrement, nous allons traiter des ensembles et des listes. La différence entre un ensemble et une liste est importante. Un ensemble est un sac qui contient des objets, sans ordre spécifique. Par contre, une liste est ordonnée. Pour représenter les ensembles, on utilise des accolades, tandis que les listes sont représentées entre parenthèses. Dans les exercices, il faudra toujours se demander si l'ordre compte (liste) ou non (ensemble). Dans les ensembles, lorsque l'ordre ne compte pas, on utilise des méthodes de combinatoire. Dans l'exemple donné, les ensembles E et F contiennent respectivement les éléments H, E, I et D, I, E, R. Pour l'union de ces ensembles (E U F), on prend tous les éléments sans répétition, et on obtient H, E, I, D et R. Pour l'intersection de ces ensembles (E ∩ F), on cherche les éléments communs, et on obtient seulement E. Le produit cartésien (E × F) est l'ensemble de toutes les paires d'éléments des deux ensembles, où l'ordre compte. Dans cet exemple, les paires possibles sont H D, H I, H E, H R, etc. Une paire est un ensemble de deux éléments. On peut former les paires possibles à partir d'un ensemble contenant trois éléments, ce qui donne les paires H E, H I et E I. Il est important de faire la distinction entre un ensemble et une liste pour compter les possibilités. N'hésitez pas à poser des questions si besoin.

Utiliser un diagramme

Les diagrammes sont un outil utile pour la compréhension visuelle des informations. Dans cet exemple, nous avons une station de sport d'hiver avec 20 touristes. Parmi eux, 14 pratiquent le ski de piste, 7 le ski de fond, et 4 pratiquent les deux activités. En utilisant un diagramme, nous plaçons les 20 touristes dans une bulle bleue. Dans cette bulle, 10 personnes pratiquent uniquement le ski de piste, 4 pratiquent à la fois le ski de piste et le ski de fond, et 3 pratiquent uniquement le ski de fond. En ajoutant ces chiffres (10 + 4 + 3), nous obtenons bien les 7 personnes qui pratiquent le ski de fond au total. Pour déterminer combien de touristes ne pratiquent aucune des activités, nous comptons simplement le nombre de personnes qui pratiquent une activité (10 + 4 + 3), puis soustrayons ce total du nombre total de touristes (20 - 17). Ainsi, nous découvrons qu'il y a 3 touristes qui ne pratiquent aucune des activités. Dans des exemples plus complexes, le principe reste le même : placer des bulles représentant différentes catégories et compter pour obtenir des chiffres précis. Les diagrammes sont donc un outil très utile pour comprendre et analyser des données.

Dénombrer des ensembles simples

Ce cours présente des exemples de dénombrement. Dans le premier exemple, on doit déterminer le nombre de résultats possibles pour lancer une pièce 7 fois de suite. En se posant les questions « est-ce que c'est une liste ou un ensemble? » et « est-ce que l'ordre compte? », on conclut que l'ordre compte et qu'on peut répéter les résultats. Ainsi, le nombre de tirages possibles est de 2 puissance 7.Dans le deuxième exemple, on doit déterminer le nombre de distributions possibles pour deux joueurs de domino recevant 7 dominos chacun parmi les 28 dominos du jeu. En considérant que l'ordre compte, le nombre de listes possibles est de 28 x 27 x 26 ... x 15 x 14. Une autre façon d'exprimer cela est 28! sur 14!.Dans le dernier exemple, on dispose de 4 gâteaux et 4 invités, et il faut attribuer un gâteau à chaque invité. Avec l'ordre compte et sans répétition, le nombre de façons de procéder est de 4!.Pour dénombrer, il faut se poser les questions « est-ce que j'ai l'ordre compte ou ne compte pas? » et « est-ce que je peux avoir répétition? ».

Tirage successif sans remise

Dans ce cours, nous abordons le concept de tirage successif sans remise. L'énoncé nous donne un exemple concret : nous avons 5 élèves qui se tiennent en rang et nous voulons savoir combien il y a de façons de les ranger. Pour résoudre ce problème, nous devons d'abord nous poser quelques questions. Est-ce une liste ou un ensemble ? Y a-t-il des répétitions possibles ? Dans ce cas, il s'agit d'une liste car l'ordre compte. Par exemple, l'ordre "1, 2, 3, 4, 5" est différent de "5, 4, 3". De plus, il n'y a pas de répétition possible car nous ne pouvons pas avoir deux fois le même élève à la même position. Maintenant que nous avons clarifié ces points, la résolution devient assez simple. Pour la première position, nous avons 5 choix possibles. Pour la deuxième position, une fois que nous avons placé quelqu'un, nous n'avons plus que 4 choix. Et ainsi de suite, jusqu'à la dernière position où nous n'avons plus qu'un seul choix. Nous multiplions donc ces choix successifs : 5 x 4 x 3 x 2 x 1, ce qui est égal à 5!. Cette formule générale s'applique également lorsque nous avons P tirages successifs sans remise dans un ensemble à N éléments. Nous pouvons l'exprimer comme suit : N! sur N-P!. En résumé, pour résoudre le problème des tirages successifs sans remise, nous utilisons la formule N! sur N-P!.

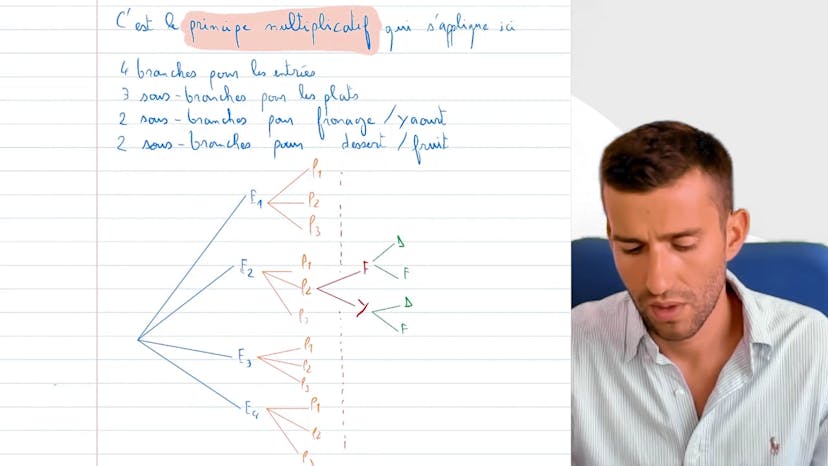
Principe multiplicatif et arbre pondéré

Apprendre à faire un arbre pondéré peut être pratique, mais cela peut prendre du temps. Si vous avez trop de sous-branches, il peut ne plus être nécessaire de faire un arbre pondéré. Au début, il est préférable de faire un brouillon de l'arbre pour clarifier les idées. Par exemple, si une cantine scolaire offre 4 entrées, 3 plats, et le choix entre fromage ou yaourt, et dessert ou fruit, il serait possible de faire un arbre pondéré. Cependant, cela peut devenir assez volumineux. Pour compter, le principe multiplicatif s'applique en faisant une multiplication de chaque possibilité. Pour le moment, il n'est pas nécessaire de se préoccuper des pondérations, mais cela sera abordé dans le chapitre suivant avec les probabilités.

Permutations : application

Dans ce cours, nous allons aborder la gestion des permutations. Une permutation peut être définie comme le nombre de façons de changer l'ordre d'une liste. Par exemple, si nous avons un tirage de loto, combien de possibilités avons-nous pour changer l'ordre de ce tirage une fois qu'il est fixé ? Nous allons prendre comme exemple une conférence avec 12 scientifiques, dont 6 hommes et 6 femmes. Parmi eux, il y a 5 mathématiciens, 3 physiciens et 4 biologistes. Chaque corps de science a décidé d'utiliser une méthode différente pour se placer. Dans tous les cas, il y a 3 méthodes différentes. La méthode des mathématiciens consiste à se placer au hasard. Dans ce cas, nous avons 12 personnes qui sont déjà fixées et nous cherchons à déterminer combien de façons de les positionner. Le nombre de permutations d'un ensemble à n éléments est donné par la formule n!. Dans notre cas, cela signifie que nous avons 12! façons de positionner ces scientifiques, ce qui correspond à environ 479 millions de possibilités. Les physiciens, quant à eux, préfèrent rester ensemble. Donc nous devons d'abord les positionner, sachant qu'ils doivent rester ensemble. Ensuite, nous pouvons permuter les positions à l'intérieur de leur groupe. Une fois que nous avons fixé la position du premier physicien, nous avons 6 façons de les positionner (3!). Ensuite, il nous reste 9 scientifiques à positionner, sans aucune contrainte, ce qui représente 9! façons de les positionner. En appliquant le principe multiplicatif, nous obtenons un total de 10 x 6 x 9! possibilités, soit environ 21 millions. Pour la méthode des biologistes, nous devons rassembler les femmes et les hommes. Il y a donc deux façons de positionner ces deux groupes. Une fois que nous avons fait ce choix, nous devons permuter les positions à l'intérieur de chaque groupe. Pour les femmes, cela représente 6! façons de les positionner, et pour les hommes, cela représente également 6! façons. En appliquant le principe multiplicatif, nous obtenons un total de 2 x 6! x 6! possibilités, soit environ 1 million 36 800. C'est ainsi que nous appliquons le comptage des permutations dans des petits exemples. Si vous avez d'autres questions, n'hésitez pas à consulter la FAQ.

Dénombrer des combinaisons

Dans ce cours, nous étudions les combinaisons en mathématiques. Une combinaison est le nombre de sous-ensembles que l'on peut obtenir à partir d'un ensemble plus grand. L'ordre n'a pas d'importance dans les combinaisons. Par exemple, au tirage du loto, l'ordre des numéros n'a pas d'importance car ce sont des cases que l'on coche. Un autre exemple est le jeu de bridge où chaque joueur reçoit une main de 13 cartes. Le nombre de mains possibles est calculé en utilisant les combinaisons. Dans cet exemple, il s'agit d'un ensemble car une fois que l'on a les 13 cartes, l'ordre n'a plus d'importance. De plus, il n'y a pas de répétitions car on ne peut pas avoir deux fois la même carte. Pour calculer le nombre de mains possibles, on peut utiliser la formule "13 parmi 52". Cela signifie choisir 13 éléments parmi un ensemble de 52 éléments. Il existe plusieurs méthodes pour effectuer ce calcul, soit en utilisant une calculatrice, soit en appliquant la formule de combinaison. Ensuite, nous pouvons analyser les mains qui contiennent uniquement un cœur. Pour cela, on choisit d'abord un cœur parmi les 13 possibilités, puis on choisit les 12 cartes restantes parmi les 39 qui ne sont pas des cœurs. On multiplie ensuite les deux résultats car il n'y a pas de notion d'ordre et on obtient le nombre de mains possibles avec un cœur. En résumé, il est important de savoir quand utiliser les combinaisons, c'est-à-dire lorsque l'ordre n'a pas d'importance et qu'il n'y a pas de répétition. Les combinaisons sont utiles pour calculer le nombre de sous-ensembles à partir d'un ensemble plus grand.

Combinaison et intersection

Dans ce cours, nous abordons l'utilisation des combinaisons avec les intersections. Nous prenons l'exemple de 20 élèves, parmi lesquels 14 aiment les maths, 7 aiment la physique et 4 aiment à la fois les maths et la physique. Pour mieux comprendre, nous utilisons un diagramme où 10 élèves aiment les maths, 4 aiment à la fois les maths et la physique, et 3 n'aiment que la physique. En déduisant cela, nous constatons qu'il y a 3 élèves qui n'aiment ni les maths ni la physique. Ensuite, nous nous intéressons aux sous-groupes d'élèves et nous cherchons combien de sous-groupes de 4 élèves peuvent être formés parmi les 14 élèves qui aiment les maths. Comme il n'y a pas d'ordre et pas de répétition, il s'agit de combinaisons. La formule à utiliser est donc "14 parmi 4", ce qui donne 14! / (4! * 10!). Si nous simplifions cette expression en supprimant les termes communs, nous obtenons 14 * 13 * 12 * 11 / (4 * 3 * 2). Ce qui équivaut à 1001. Ensuite, nous nous demandons combien de sous-groupes de 4 élèves ont exactement 2 élèves qui n'aiment que les maths et 2 élèves qui n'aiment que la physique. Pour cela, nous divisons le sous-groupe en deux parties, l'une avec les élèves qui n'aiment que les maths (10 élèves) et l'autre avec ceux qui n'aiment que la physique (3 élèves). Nous cherchons donc "2 parmi 10" et "2 parmi 3". En simplifiant ces expressions, nous obtenons 2 * 9 / 2 et 3. Le total est donc de 135 possibilités. Ainsi, nous avons vu comment combiner les notions de combinaisons et d'intersections pour résoudre des problèmes décombinatoires.

Classique : jetons colorés

La méthode de dénouement utilisée dans ce cours consiste à faire un bilan des différentes variantes des jetons de couleurs utilisés. Les couleurs des jetons sont indiscernables, mais il y a des jetons blancs avec le numéro 0 et des jetons rouges avec le numéro 7. Pour commencer, on tire simultanément 4 jetons, ce qui signifie qu'il n'y a pas d'ordre dans le tirage. On calcule ensuite le nombre de tirages possibles, en utilisant la formule des combinaisons. Dans ce cas, il y a 20 jetons au total et on en tire 4, donc il y a 4845 tirages possibles. Ensuite, on s'intéresse aux tirages avec les quatre jetons ayant le même numéro. Il faut donc identifier les numéros qui sont présents au moins quatre fois parmi les jetons. Dans ce cas, les seuls numéros qui satisfont cette condition sont 0, 2 et 7. On compte alors le nombre de choix possibles pour chaque numéro et on additionne les résultats. Cela donne 67 tirages possibles. La troisième question concerne les tirages avec uniquement des jetons blancs. On compte le nombre de jetons blancs disponibles (12) et on utilise la formule des combinaisons pour calculer le nombre de tirages possibles avec 4 jetons parmi ces 12. Il y a donc 495 tirages possibles. Pour le quatrième cas, on cherche le nombre de tirages avec des jetons de la même couleur. On identifie les couleurs qui sont représentées avec plus de 4 jetons, ce qui donne les couleurs blanc et rouge. On compte le nombre de choix possibles pour chaque couleur et on additionne les résultats. Cela donne 565 tirages possibles. Ensuite, il est demandé de former le nombre 2020 avec les jetons tirés. Comme l'ordre n'a pas d'importance dans un tirage simultané, on peut le considérer comme 2200 ou 0022. Il faut donc trouver le nombre de tirages possibles avec 2 jetons avec le numéro 2 parmi les 8 jetons disponibles et 2 jetons avec le numéro 0 parmi les 4 jetons disponibles. Cela donne 268 tirages possibles. Enfin, on demande combien de tirages comportent au moins un jeton avec un numéro différent des autres. Plutôt que de chercher cet événement directement, il est plus simple de considérer l'événement contraire, c'est-à-dire des tirages avec tous les jetons identiques. On a déjà calculé le nombre de tirages de ce type, qui est de 76. On soustrait donc ce nombre du nombre total de tirages possibles pour obtenir le résultat final de 4739 tirages possibles.

Cours par cas pratiques !

Dans ce cours, nous apprenons à déterminer le nombre d'anagrammes pour différents mots. Un anagramme est une combinaison de lettres d'un mot, où l'ordre des lettres importe. Par exemple, pour le mot ABC, les anagrammes possibles sont BAC, CBA, CAB, etc. Pour calculer le nombre d'anagrammes, nous utilisons la notion de permutations. Le nombre d'anagrammes d'un mot est égal au nombre de façons de ranger les lettres du mot. Par exemple, pour le mot ABC, il y a 3! (3 factorielle) possibilités, car il y a 3 lettres et 3 cases pour les ranger. Cependant, lorsque certaines lettres sont répétées, nous devons prendre en compte les permutations de ces lettres. Par exemple, pour le mot AXA, il y a 3! possibilités au départ, mais nous divisons le résultat par 2, car les deux A peuvent être permutés de deux manières différentes. De manière plus générale, pour un mot comme CHIEN, nous calculons d'abord le nombre d'anagrammes sans tenir compte des lettres répétées (5! dans ce cas), puis nous divisons le résultat par le produit des factorielles des nombres de permutations possibles pour chaque lettre répétée. Par exemple, pour le mot ABRACADABRA, il y a 11! possibilités au départ, mais nous devons diviser le résultat par 5! (pour les A), 2! (pour les B) et 2! (pour les R), car ces lettres sont répétées. Cette méthode permet de calculer efficacement le nombre d'anagrammes pour différents mots en prenant en compte les lettres répétées.

Exo type en une minute !

Ce cours porte sur un test composé de quatre questions indépendantes, avec des réponses vrai ou faux. Le candidat répond au hasard, sans connaître les réponses. La question est de déterminer la probabilité pour le candidat d'obtenir les quatre réponses correctes, ou plus précisément, combien de scénarios mèneraient à cette réussite. En utilisant la formule de calcul des puissances, on trouve qu'il y a 16 choix possibles au total. Donc, si vous répondez au hasard, il y a une chance sur 16 d'obtenir les quatre réponses correctes. Cette petite expérience est intéressante et amusante.