Cours d'apprentissage en ligne

Simplifier des expressions

Dans ce cours, nous traitons des propriétés et des méthodes pour résoudre des inéquations avec des exponentielles et des logarithmes. Voici un résumé SEO-friendly des différentes équations et inéquations traitées dans la vidéo : 1. Équation : ln(x) = 2 - Composez par l'exponentielle pour obtenir x = e^2. 2. Équation : e^x + 1 = 5 - Composez par le logarithme pour obtenir x + 1 = ln(5). - Résolvez pour x en soustrayant 1 de chaque côté : x = ln(5) - 1. 3. Équation : 3ln(x) - 4 = 8 - Divisez par 3 pour obtenir ln(x) - 4/3 = 8/3. - Composez par l'exponentielle pour obtenir x = e^(4/3). 4. Inéquation : ln(6x - 1) > 2 - Vérifiez que l'expression à l'intérieur du logarithme est strictement positif (6x - 1 > 0). - Composez par l'exponentielle pour obtenir 6x - 1 > e^2. - Résolvez pour x en trouvant que x > (e^2 + 1)/6. 5. Inéquation : e^x + 5 > 4e^x - Rassemblez tous les termes exponentiels ensemble pour obtenir e^x < 5/3. - Composez par le logarithme pour obtenir x < ln(5/3). 6. Équation : ln(x - 3) + ln(9 - x) = 0 - Rassemblez les termes logarithmiques pour obtenir ln((x - 3)(9 - x)) = 0. - Composez par l'exponentielle pour obtenir (x - 3)(9 - x) = 1. - Résolvez l'équation quadratique pour trouver les solutions x1 = 6 + racine(8) et x2 = 6 - racine(8). - Vérifiez que ces solutions sont dans l'intervalle valide (3, 9). 7. Inéquation : ln(3 - x) - ln(x + 1) < 0 - Vérifiez les valeurs possibles pour x (3 - x > 0 et x + 1 > 0), ce qui donne -1 < x < 3. - Rassemblez les termes logarithmiques en utilisant la propriété ln(a) - ln(b) = ln(a/b) pour obtenir ln((3 - x)/(x + 1)) < 0. - Composez par l'exponentielle pour obtenir (3 - x)/(x + 1) < 1. - Multipliez par (x + 1) sans changer le sens de l'inégalité (car (x + 1) > 0), ce qui donne 3 - x < x + 1. - Résolvez l'inéquation pour trouver x > 2. Il est important de toujours considérer l'ensemble de définition de l'équation ou de l'inéquation traitée afin d'exclure les solutions invalides. Il est également essentiel de faire attention aux signes lors de la manipulation d'équations et d'inéquations. Le regroupement des termes logarithmiques et exponentiels est une méthode utile pour résoudre ces types de problèmes.

Équations Inéquations

Ce cours sur les inéquations avec logarithmes explique comment résoudre une équation donnée en isolant le terme en ln. Après avoir vérifié l'ensemble de définition de l'inéquation, l'objectif est de composer par l'exponentiel pour isoler le ln. Ensuite, on résout l'équation simple obtenue et on prend en compte l'ensemble de définition initial pour déterminer l'intervalle solution. Attention à bien faire correspondre les ensembles de définition pour éviter les erreurs. Cette méthode consiste donc à isoler le terme en logarithme, composer par l'exponentiel et prendre l'intersection de la solution finale avec l'ensemble de définition initial.

Exposant=Inconnue ?

Ce cours traite de l'utilisation de l'exponentiel et du logarithme pour résoudre des inéquations avec des exposants. Il mentionne que ces calculs sont notamment utilisés en physique, par exemple pour déterminer la durée à partir de laquelle une certaine quantité d'atomes radioactifs a disparu. Pour résoudre ces équations, on utilise la définition de l'exponentiel pour les puissances. Lorsque l'exposant n'est pas un entier, il est défini comme étant égal à e^(B ln A), où e est la constante d'Euler et ln désigne le logarithme népérien. A partir de cette définition, on résout les équations en utilisant les propriétés du logarithme. Il est important de vérifier la cohérence des signes lors de la résolution des équations.

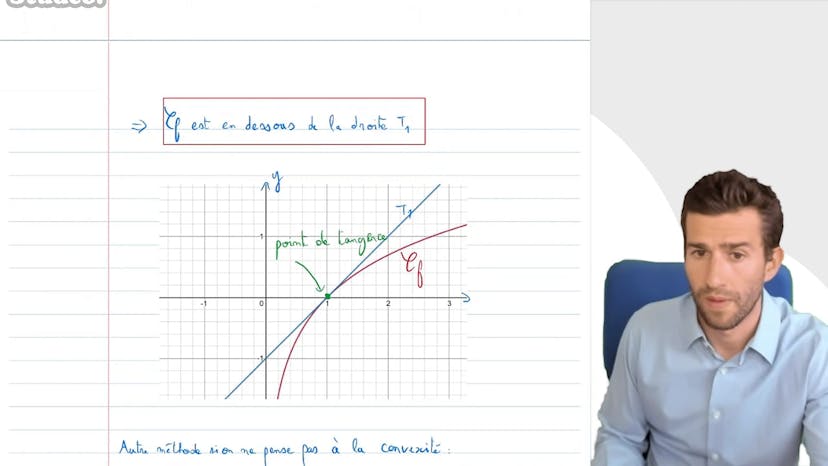
Courbe et Tangentes

Ce cours traite de l'étude du logarithme et de sa tangente en un point précis. On nous demande de trouver l'équation de la tangente au point d'abscisse 1. La fonction logarithme est dérivable sur R*, sa dérivée est 1/x et évaluée en 1, cela donne 1. La position relative de la courbe par rapport à sa tangente peut être déterminée en étudiant la concavité de la fonction. La dérivée seconde est 1/x^2 et est strictement négative pour tout x positif. Cela signifie que la fonction est concave et donc en dessous de toutes ses tangentes, y compris celle au point d'abscisse 1. Une autre approche consiste à étudier les variations de la fonction en calculant sa dérivée. On pose une fonction auxiliaire g(x) = ln(x) - x + 1. En étudiant le signe de g'(x) = 1/(x-1), on peut construire un tableau de variations qui montre que g(x) est inférieure à 0 pour tout x, avec égalité en x=1. En conclusion, la tangente au point d'abscisse 1 de la fonction logarithme a pour équation y = x - 1. Il est préférable de considérer la concavité de la fonction pour déterminer la position relative de la courbe par rapport à sa tangente.

On redécouvre le log ?!

Dans ce cours, on nous demande de déterminer les fonctions qui vérifient f2ab = f2a + f2b et f'(1) = 1. On remarque que la relation fonctionnelle du logarithme ressemble à cette équation. On va donc essayer de redémontrer certaines propriétés du log. Tout d'abord, on démontre que pour toute fonction f non nulle, il n'est pas possible de définir la fonction en 0. On suppose que cela est possible et on utilise la relation donnée pour trouver que f(0) = 0. Si on prend b = 0 et a non nulle, on obtient f(a) = 0. Donc pour tous les réels possibles, f est égal à 0. Cela contredit notre hypothèse de départ que f est non nulle. Donc la fonction ne peut pas être définie en 0. Ensuite, on montre que f(1) = 0. On remplace a et b par 1 dans la relation donnée et on trouve que 2f(0) = f(0), donc f(0) = 0. Enfin, on démontre que f(x/y) = f(x) - f(y). On remarque que cette équation ressemble à la démonstration de log(a/b) = log(a) - log(b). On réapplique la même méthode et on trouve que f(x/y) = -f(y). Cela nous permet de conclure que f(x/y) = f(x) - f(y). En résumé, on a montré que si une fonction vérifie f(2ab) = f(2a) + f(2b) et f'(1) = 1, alors cette fonction a toutes les propriétés du logarithme. On peut donc dire que ces deux conditions suffisent pour définir fondamentalement le log.

Une nouvelle définition de l'exp

Le cours aborde des concepts plus techniques en mathématiques, en particulier sur les logarithmes et les limites. Il explique la propriété principale du logarithme, qui est que le logarithme d'une puissance de A est égal à N fois le logarithme de A. Cette propriété permet de simplifier les expressions mathématiques complexes impliquant des puissances. Le cours souligne également l'importance de connaître les propriétés des logarithmes et des limites pour résoudre des problèmes plus avancés. L'utilisation du logarithme peut aider à simplifier les expressions et à trouver des limites. Le cours montre comment utiliser les propriétés des logarithmes pour démontrer que certaines expressions sont bien définies et pour calculer des limites. Il utilise également des formules du cours pour manipuler les expressions mathématiques et trouver des équivalences. Enfin, le cours conclut en montrant que la limite de log de U, N est égale à A, ce qui démontre l'équivalence entre l'exponentielle et le logarithme. En résumé, le cours explique l'utilisation des logarithmes pour simplifier les expressions mathématiques et trouver des limites. Il met en évidence l'importance de connaître les propriétés des logarithmes et des limites pour résoudre des problèmes plus avancés en mathématiques.

Dérivabilité et Variations

Le cours porte sur l'étude d'une fonction logarithmique. La fonction donnée est ln(2x)/(ln(2x)-1). Elle est définie pour x appartenant à (0, +∞), à l'exception de x = e. Pour étudier cette fonction, on applique la méthode classique de dérivation. La dérivée de la fonction est g'(x) = -2x/(ln(2x)-1)². On observe que g'(x) est strictement négatif sur son domaine de définition. Par contre, il y a une valeur interdite en x = e, où le dénominateur s'annule. Par conséquent, la fonction est décroissante sur (0, e) et sur (e, +∞), mais il y a un décrochage à x = e. Lorsqu'il y a une valeur interdite, il est courant d'avoir une division par zéro, où la fonction diverge vers l'infini positif d'un côté et vers l'infini négatif de l'autre. Ainsi, le tableau de variations complet est obtenu en analysant les limites de g en 0, e-, e+, et +∞. On remarque qu'en 0, g(x) tend vers 1. En e-, g(x) tend vers -∞, tandis qu'en e+, g(x) tend vers +∞. Finalement, en +∞, g(x) tend également vers 1. Le graphe de la fonction présente une asymptote verticale en x = e et une asymptote horizontale en y = 1. La courbe est décroissante jusqu'à x = e, puis remonte vers l'infini. Il est essentiel de noter qu'il y a un saut de -∞ à +∞ à l'asymptote verticale.

Croissance Comparée

Dans ce cours, nous étudions la fonction f(x) = 3-x + 2ln(2x). Nous commençons par dériver cette fonction pour trouver son signe. La dérivée f'(x) = -1 + 2x nous permet de déterminer que la fonction est positive pour x > 1 et négative pour x < 1. Pour x > 0, la dérivée est également positive jusqu'à x = 2, ensuite elle devient négative. Ainsi, nous pouvons conclure que f(x) est croissante sur l'intervalle (0, 2) et décroissante sur l'intervalle (2, +∞). Ensuite, nous calculons également f(2) pour avoir une vue d'ensemble de la variation de f. Nous obtenons f(2) = 1 + 2ln(2). Pour étudier plus en détail la variation de f, nous analysons les limites de la fonction. Lorsque x tend vers +∞, nous factorisons par le terme prédominant - x, ce qui nous permet de simplifier l'expression et de conclure que la limite est égale à 0. De même, lorsque x tend vers 0, nous arrivons à la conclusion que la limite est également égale à 0. Ainsi, le tableau de variation complet de f est établi. Enfin, nous étudions la convexité de f en calculant la dérivée seconde f''(x) = -1/x^2. En résolvant cette équation, nous trouvons que f''(x) = 0 pour x ≠ 0. Cela signifie que f est concave sur l'ensemble de son domaine de définition, c'est-à-dire R étoile plus. En résumé, la fonction f(x) = 3-x + 2ln(2x) est croissante sur (0,2) et décroissante sur (2, +∞). Elle a un maximum en 2 et est concave sur R étoile plus tout entier.

Ln : Limites

Dans ce cours, nous nous intéressons aux calculs de limites faisant intervenir la fonction ln (logarithme népérien). Le principe est de factoriser par le terme prédominant pour simplifier les limites. Pour les limites avec ln, nous essayons de les ramener à des limites usuelles sur le logarithme. Voici trois exemples : 1. Limite de 2ln2x²-5ln2x±1 : En factorisant par ln2x², nous obtenons une limite qui tend vers l'infini. 2. Limite de ln(racine de x) / ln(2x) : En utilisant les propriétés du logarithme, nous transformons la limite en xlnx/ln2 + lnx. Après une factorisation par ln x, nous obtenons une limite de 1.5. 3. Limite de (x-1)²ln(x-1) : En posant grand x = x-1, nous ramenons la limite à une limite usuelle de x²lnx. Puisque cette limite tend vers 0, nous obtenons que la limite recherchée est égale à 0. Ces exemples illustrent comment calculer des limites avec le logarithme.

Dériver ln(u)

Le cours traite de la définition du logarithme et de la façon de déterminer l'ensemble de définition d'une fonction contenant un logarithme. Ensuite, il explique comment calculer la dérivée de cette fonction. Le cours donne plusieurs exemples pour illustrer ces concepts. Pour la première fonction, f(x) = ln(8x-4), l'ensemble de définition et de dérivabilité est [1.5, +∞[. La dérivée de cette fonction est f'(x) = 2/(2x-1). Pour la deuxième fonction, f(x) = ln(x² + x + 1), l'ensemble de définition et de dérivabilité est ℝ. La dérivée de cette fonction est f'(x) = 2x/(x² + x + 1). Pour la troisième fonction, f(x) = ln(x-1) - ln(2x+4), l'ensemble de définition et de dérivabilité est ]-∞, -2[ ∪ ]1, +∞[. La dérivée de cette fonction est f'(x) = (6)/(2(x-1)(2x+4)). Pour la dernière fonction, f(x) = ln(e^x), l'ensemble de définition et de dérivabilité est ]0, +∞[. La dérivée de cette fonction est f'(x) = 1. En résumé, il est important de toujours prendre en compte l'ensemble de définition d'une expression contenant un logarithme et de calculer la dérivée de manière appropriée.

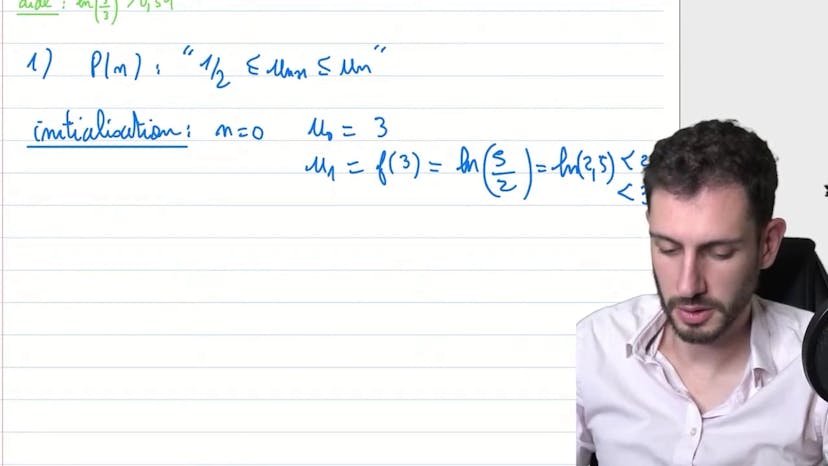
Fonction et suite récurrente associée

Dans ce cours, nous étudions une fonction définie de manière rationnelle, c'est-à-dire avec un degré 1 au-dessus et un degré 1 en dessous de la fraction. La fonction est définie sur l'intervalle de 0 à l'infini. Nous déterminons la limite de cette fonction lorsque x tend vers l'infini en utilisant la composition de fonctions. La limite est égale au logarithme de 3. En utilisant la continuité du logarithme, nous concluons que la fonction est bien définie. Ensuite, nous démontrons que la dérivée de la fonction est égale à 3x+3 pour tout nombre réel positif ou nul. Nous concluons que la fonction est strictement croissante et positive. Ensuite, nous passons à l'étude d'une suite définie par récurrence à l'aide de cette fonction. Nous démontrons par récurrence que la suite est décroissante et minorée par un demi. En utilisant le théorème de convergence des suites décroissantes et minorées, nous concluons que la suite converge vers une limite strictement positive. En résumé, ce cours traite de la définition d'une fonction rationnelle, de la détermination de sa limite, de la démonstration de la dérivée de la fonction, de l'étude d'une suite définie par récurrence à l'aide de cette fonction et de la convergence de cette suite.