Cours d'apprentissage en ligne

Peu d'infos : trouver un max

Dans ce cours, on étudie une fonction continue f(x) sur R (l'ensemble des nombres réels) telle que sa limite lorsque x tend vers moins l'infini et sa limite lorsque x tend vers plus l'infini sont tous deux infinis. L'objectif est de démontrer que f admet un minimum sur R. Nous commençons par remarquer intuitivement que si f tend vers l'infini lorsque x tend vers moins l'infini et plus l'infini, il doit exister un minimum à un certain moment, étant donné la continuité de f. Cependant, nous devons le démontrer de manière rigoureuse. Pour ce faire, nous utilisons la propriété des limites. Nous choisissons un point a où nous appliquons les définitions des limites. Nous posons alors a = f(2,0). Grâce à cette démarche, nous pouvons trouver un nombre M1 strictement supérieur à 0 tel que si x est supérieur à M1, f(2, x) est supérieur à f(2,0) (limite en plus l'infini). De même, nous trouvons un nombre M2 strictement inférieur à 0 tel que pour tout x inférieur ou égal à M2, f(2, x) est supérieur ou égal à f(2,0) (limite en moins l'infini). En choisissant a = f(2,0), nous savons que f(2,0) se situe entre M1 et M2. Nous avons ainsi défini notre segment [M1, M2] sur lequel f est continue et donc bornée. De plus, il existe un x0 tel que f(2, x0) soit supérieur à f(2, x0,0), ce qui signifie qu'il y a un minimum sur ce segment. Puisque 0 appartient à [M1, M2], nous pouvons affirmer que quel que soit x en dehors de ce segment, f(2, x) est supérieur ou égal à f(2, x0,0). Ce résultat est obtenu grâce à la relation étroite étoile. Ainsi, nous sommes en mesure de dire que f(2, x) est supérieur ou égal à f(2, x0,0) sur tout R, excepté le segment [M1, M2]. En conclusion, f admet bien un minimum sur R. C'est la fin de cet exercice et à bientôt pour la suite !

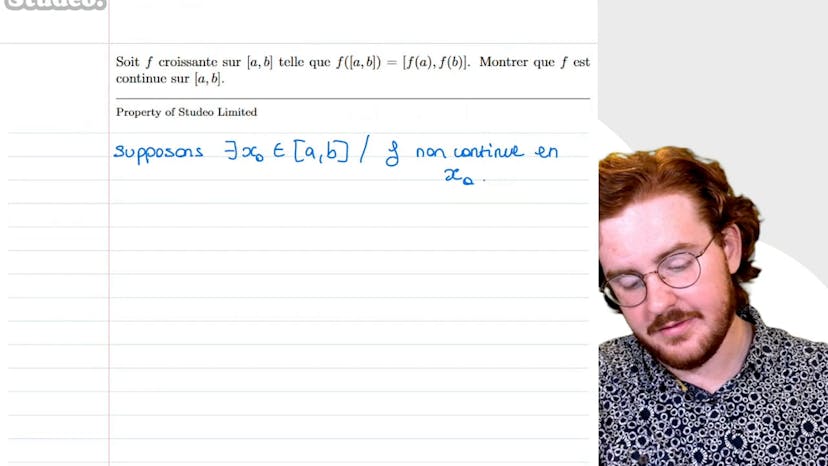
Ensemble image et continuité

Salut, dans ce cours, nous allons montrer que la fonction f est continue sur le segment AB. Pour cela, nous allons supposer par l'absurde qu'il existe un point x0 dans A et B où f n'est pas continue. Comme f est croissante et bornée sur A et B, les limites L- et L+ existent et sont finies. Si f était continue en x0, alors L- serait égal à L+. Cependant, puisque f n'est pas continue en x0, L- est différent de L+. En utilisant la croissance de f, nous pouvons montrer que pour tout x dans A et x0, f(x) est inférieur ou égal à L-. De même, pour tout x dans x0 et B, f(x) est supérieur ou égal à L+. Comme L- et L+ sont différents, il existe un alpha compris entre L- et L+ qui n'appartient pas à l'image de f sur AB. Cependant, alpha appartient à AB, ce qui crée une contradiction. Par conséquent, f est continue sur le segment AB. C'est la fin du cours, à bientôt !

En construction !

Aucun résumé n'est disponible pour cette vidéo

Parité

Dans cette vidéo, Corentin aborde le concept des fonctions paires et impaires. Il présente quatre fonctions différentes: un polynôme de degré 4, une fraction rationnelle, une somme de fonctions trigonométriques et une autre fonction trigonométrique. Il commence par rappeler la définition d'une fonction paire, qui est vérifiée lorsque pour tout élément x dans son domaine de définition, x est également dans le domaine de définition et f (-x) = f (x). De même, une fonction est impaire si la première condition est vérifiée et f (-x) = - f (x). En analysant le premier polynôme, il remarque que son domaine de définition est ℝ (l'ensemble des nombres réels) et que pour tout x dans ℝ, l'opposé de x est également dans ℝ. Ainsi, la première condition est vérifiée et en calculant f (-x), il trouve que f (-x) = f (x). Donc, cette fonction est paire. Ensuite, il passe à la deuxième fonction, une fraction rationnelle. Il constate que -1 appartient au domaine de définition de la fonction, mais que 1 n'y appartient pas, car il annule le dénominateur. Par conséquent, cette fonction n'est ni paire ni impaire, car la première condition n'est pas vérifiée. Il poursuit avec la troisième fonction, une somme de fonctions trigonométriques. Il rappelle que la somme de deux fonctions paires est paire et que la somme de deux fonctions impaires est impaire. En analysant les fonctions individuellement, il remarque que le cosinus de 2x est impaire et que la tangente de x est également impaire. Par conséquent, selon le rappel, la fonction f₁₋₃ associée au cosinus de 2x plus la tangente de 2x est impaire. Enfin, il aborde la dernière fonction, f₁₋₄, qui est la somme du cosinus de 2x et du sinus de 2x. Il constate que f₁₋₄ (π/4) = cosinus (π/4) + sinus (π/4) = 1,5, mais que f₁₋₄ (-π/4) = cosinus (-π/4) + sinus (-π/4). Étant donné que le cosinus est pair et que le sinus est impaire, le terme avec le cosinus peut être simplifié et il conclut que f₁₋₄ (-π/4) = 0. Ainsi, f₁₋₄ n'est pas paire ni impaire. En résumé, le polynôme de degré 4 est paire, la fraction rationnelle n'est ni paire ni impaire, la somme de fonctions trigonométriques est impaire et la somme du cosinus de 2x et du sinus de 2x n'est ni paire ni impaire.

Décomposition d’une fonction en fonction paire et impaire

Dans cet exercice, nous devons montrer que la fonction F peut s'écrire de manière unique comme la somme d'une fonction paire et d'une fonction impaire. Pour cela, nous utilisons un raisonnement par analyse synthèse. Dans la première partie de l'analyse, nous supposons que F s'écrit effectivement comme la somme d'une fonction paire G et d'une fonction impaire H. En utilisant la parité de G et l'imparité de H, nous obtenons un système linéaire à deux inconnus à résoudre. Nous trouvons que G de X est égal à F de X plus F de moins X sur 2, et que H de X est égal à F de X moins F de moins X sur 2. Dans la partie de la synthèse, nous supposons l'existence de deux autres fonctions paire et impaire, G1, G2 et H1, H2 respectivement, qui s'écrivent également comme la somme de F. En utilisant à nouveau la parité de G et l'imparité de H, nous obtenons un système linéaire similaire. En le résolvant, nous trouvons que G1 est égal à G2 de X, qui est égal à F de X plus F de moins X sur 2, et H1 est égal à H2 de X, qui est égal à F de moins X moins F de moins X sur 2. Ainsi, nous avons montré que le couple de fonctions paire et impaire G, H est unique. Par conséquent, F peut s'écrire de manière unique comme la somme d'une fonction paire G et d'une fonction impaire H, où G de X est égal à F de X plus F de moins X sur 2, et H de X est égal à F de X moins F de moins X sur 2.

Axes de symétrie d’une fonction

Dans cette vidéo, Corentin aborde les notions fondamentales d'axes et de centres de symétrie. Il commence par lire l'énoncé qui se compose de quatre questions. La première question demande de montrer que la droite d'équation x=3/2 est un axe de symétrie du graphe de la fonction f(x) = x²-3x+2. La deuxième question demande de montrer que le point (1,2) est un centre de symétrie du graphe de la fonction f(x) = (2x+1)/(x-1). La troisième question demande de montrer que le point (0,5) est un centre de symétrie du graphe de la fonction f(x) = exp(x)/(exp(x)+1). Enfin, la quatrième question demande d'étudier les symétries de la courbe représentative de la fonction f(x) = cos(x) + cos(3x). Pour répondre à ces questions, Corentin commence par rappeler la définition d'un axe de symétrie (pour la première question) et d'un centre de symétrie (pour les questions 2 et 3). Il effectue ensuite les calculs nécessaires pour montrer que les valeurs demandées (3/2 pour la première question, (1,2) pour la deuxième question et (0,5) pour la troisième question) sont bien des axes ou centres de symétrie des fonctions données. Enfin, pour répondre à la quatrième question, il remarque une périodicité dans la fonction f(x) et conclut que les axes de la forme x=2kπ (où k est un nombre entier) sont des axes de symétrie de f(x). Il utilise ensuite des calculs pour confirmer cette conclusion. Il souligne également que les fonctions peuvent avoir plusieurs axes de symétrie, d'où l'utilisation de la notation x=2kπ pour montrer qu'un axe est un axe de symétrie.

Fonction bornée

Aucun résumé n'est disponible pour cette vidéo

Parité et dérivation

Aucun résumé n'est disponible pour cette vidéo

Equation fonctionnelle

Dans cette vidéo, Corentin résout une équation fonctionnelle qui fait peur à beaucoup de personnes. Il doit trouver toutes les fonctions continues de 0 à 1 dans R qui vérifient une certaine équation. Pour cela, il utilise des tests avec des fonctions classiques telles que f(x) = 0, f(x) = constante, f(x) = x, f(x) = exponential de x ou logarithme de x. Il remarque que seule la fonction f(x) = 0 fonctionne. Il décide alors de prouver cette assertion par l'absurde et suppose que f est différente de 0. Il utilise le fait que la fonction f est continue sur un segment et atteint ses bornes (théorème fondamental de l'analyse) pour montrer que f ne peut pas être différente de 0. Il conclut donc que la seule fonction qui résout l'équation est f(x) = 0. Le problème n'était finalement pas si compliqué.

Équation Tangente

Ce cours porte sur la détermination des équations de tangentes, une méthode classique en mathématiques. Il est important de bien maîtriser cette méthode car elle est souvent utilisée dans les exercices d'étude de fonctions pour analyser les tangentes et la position relative de la courbe par rapport à ces tangentes. Dans cet exercice, on nous demande d'étudier une fonction f(x) = x^2 + 3x + 1 et de calculer f'(2) et f(2). Après calcul, on trouve que f(2) = 11 et f'(2) = 7. En utilisant la formule y = f'(A)x + f(A) (A ici étant égal à 2), on trouve l'équation de la tangente : y = 7x + 3. Il est intéressant de comprendre d'où vient cette formule. Pour cela, on peut réexprimer une équation de droite y = mx + p en utilisant les coordonnées du point de tangence A (qui ici est 2, f(2)) et la pente de la tangente (qui est égale à la dérivée de f en A). On obtient ainsi l'équation y = f'(A)x + (f(A)-Af'(A)). Finalement, nous devons étudier une autre question concernant la fonction g(x) = e^x et l'équation de sa tangente en un point donné (ici le point (0,1)). Après calcul, on trouve l'équation de la tangente : y = x + 1. En résumé, ce cours nous a permis d'apprendre la méthode de détermination des équations de tangentes, une compétence essentielle dans l'étude des fonctions.

Formules Classiques

Dans ce cours, il est rappelé l'importance de connaître parfaitement les formules de dérivation, car des erreurs sur ces formules peuvent entraîner de mauvais résultats dans un contrôle ou un examen. Il est donc essentiel d'être sûr de ses formules. Quelques exemples sont donnés pour illustrer le fonctionnement des dérivées. Pour une fonction de la forme x^n, la dérivée est n fois x^(n-1). Pour une fonction de la forme √x, la dérivée est (1/2)√x. Pour une fonction de la forme 1/v, la dérivée est -v'/(v^2). Pour une fonction de la forme uv, la dérivée est u'v + uv'. Il est conseillé de factoriser autant que possible lors des calculs, sauf si cela s'avère compliqué. Il est également recommandé de développer et de regrouper les termes de même degré pour faciliter les calculs et éviter les erreurs. Une méthode systématique de sélection des termes peut être utile pour être sûr de ne pas en oublier. En conclusion, il est rappelé l'importance de bien maîtriser les formules de dérivation et de s'entraîner régulièrement pour les mémoriser.