 Tous les sujets
Tous les sujets Maths
Maths Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée Prépa Examens
Prépa Examens
Terminale
Première
Seconde
MPSI/PCSI
2BAC SM Maroc
 Tous les sujets
Tous les sujets Maths
Maths Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée Prépa Examens
Prépa Examens
Maths
Algèbre
MPSI/PCSI

Equation type Fermat
Dans cet exercice, on doit résoudre une équation avec des coefficients entiers. On nous demande de montrer que si n, a et b sont des entiers tels que n est un multiple de 4 et que l'équation n = a² + b² est vérifiée, alors a et b doivent être pairs.
Pour prouver cela, on va utiliser une preuve par l'absurde. On suppose d'abord que a et b sont impairs. On peut alors écrire a comme 2k + 1 et b comme 2k' + 1, où k et k' sont des entiers. On développe ensuite l'équation a² + b² et on factorise par 4. On remarque que cela nous donne 4 fois un nombre entier plus 2. Cependant, cela implique que a² + b² est congru à 2 modulo 4, ce qui contredit le fait que n est un multiple de 4. Donc, l'hypothèse selon laquelle a et b sont impairs est fausse.
Ensuite, on suppose qu'un des deux nombres a ou b est impair. Nous pouvons supposer sans perte de généralité que c'est a qui est impair et que b est pair. En utilisant le même raisonnement, on arrive à la conclusion que a et b doivent tous les deux être pairs pour que n soit un multiple de 4.
En utilisant cette conclusion, on peut également montrer que l'équation 2^(2n) = a² + b² n'a pas de solution. En supposant qu'il existe une solution et en notant n0 le plus petit entier tel que 2^(2n0) = a² + b², on montre de manière contradictoire que cette équation n'a pas de solution en utilisant la minimalité de n0.
Enfin, on nous demande de démontrer que l'équation 2^(2n) + 1 = a² + b² a une unique solution. On montre d'abord qu'une solution est donnée par a = b = 2^n en décomposant 2^(2n) + 1 en 2 (2^n)^2. Ensuite, on utilise une preuve par récurrence pour montrer que c'est la seule solution. On suppose que cela est vrai pour un certain rang n et on montre que cela est aussi vrai pour n+1, en utilisant le fait que 2^(2n+3) est un multiple de 4 et en appliquant notre hypothèse de récurrence.
Ainsi, on peut conclure que l'équation 2^(2n) + 1 = a² + b² admet une unique solution donnée par a = b = 2^n.
Maths
Algèbre
MPSI/PCSI

Divisbilté par 7
Dans cet exercice, il s'agit de démontrer que pour tout nombre naturel n, l'expression 3 puissance 2n plus 1 plus 2 puissance 4n plus 2 est divisible par 7.
Pour cela, on utilise une méthode de récurrence. On commence par le cas initial, n=0. En substituant n par 0 dans l'expression, on obtient 3 puissance 1 plus 2 puissance 2, qui est égal à 7. Donc, dans ce cas, 7 divise bien l'expression.
Ensuite, on passe au cas de n à n+1. On veut montrer que l'expression 3 puissance 2n plus 3 plus 2 puissance 4n plus 6 est congruente à 0 modulo 7. Pour cela, on utilise les congruences. On factorise l'expression en extrayant 3 puissance 2 et 2 puissance 4 (car un 2 et un 4 sont sortis lors du passage de n à n+1). En utilisant les propriétés des congruences modulo 7, on peut simplifier l'expression et la réécrire comme 2 * (3 puissance 2n plus 1 plus 2 puissance 4n plus 2).
Or, on reconnaît que cette expression est congruente à 0 modulo 7, grâce à l'hypothèse de récurrence. En effet, on sait que pour tout n antinaturel, l'expression 3 puissance 2n plus 1 plus 2 puissance 4n plus 2 est divisible par 7. Donc, si cette expression est congruente à 0 modulo 7, l'expression 3 puissance 2n plus 3 plus 2 puissance 4n plus 6 l'est également.
Finalement, on a bien démontré que pour tout n, l'expression 3 puissance 2n plus 1 plus 2 puissance 4n plus 2 est divisible par 7.
Maths
Algèbre
MPSI/PCSI

Congurences simultanées
Dans cet exercice, nous devons résoudre des équations linéaires congruentes modulo m.
Dans la première partie, on nous demande de prouver qu'une équation de la forme nx congrue à a modulo m a une unique solution modulo m lorsque n et m sont premiers entre eux.
On utilise le théorème de Bézout qui nous dit que si m et n sont premiers entre eux, alors il existe une combinaison linéaire d'entiers u et v telle que mu plus nv est égal à 1.
On multiplie l'équation nx congrue à a modulo m par v de chaque côté pour se débarrasser de nv et obtenir x congrue à av modulo m.
Dans la deuxième partie, on considère deux équations modulo n et m respectivement, avec m et n premiers entre eux. On veut montrer qu'il existe une unique solution modulo nm.
On utilise à nouveau le théorème de Bézout pour trouver une combinaison linéaire d'entiers u et v telle que um plus nv est égal à 1.
En multipliant la deuxième équation par nv, on obtient une expression pour k, qui est égal à v fois b moins a modulo m. On remplace k dans la première équation pour obtenir une expression pour x.
La solution est donc de la forme x congrue à av modulo mn.
Ensuite, dans la troisième partie, on résout un problème pratique où deux signaux s'allument à des intervalles de temps différents.
On modélise ce problème par trois congruences modulo 15, 28 et 2 respectivement. On utilise le théorème de Bézout pour trouver une unique solution, qui est x congrue à 92 plus 420L modulo 420, où L est un entier arbitraire.
Finalement, dans la dernière partie, on résout un problème où on doit répartir un butin entre plusieurs personnes.
On modélise ce problème par trois congruences modulo 17, 11 et 6 respectivement. On utilise le théorème de Bézout pour trouver une solution particulière, qui est x congrue à 37 modulo 187.
En résolvant cette équation modulo 6, on trouve que l'ensemble des solutions est x congrue à 785 plus 1122L modulo 1122, où L est un entier arbitraire.
Maths
Algèbre
MPSI/PCSI

PGCD Fibonacci
Dans cet exercice, nous étudions la suite de Fibonacci. Nous rappelons que la suite de Fibonacci est définie par U0=0, U1=1 et Un+2 = Un+1 + Un.
La première question consiste à montrer que pour tout n positif, (Un+1 * Un-1 - Un^2) = (-1)^n. Pour cela, nous considérons une suite Vn définie par Vn = (Un+1 * Un-1 - Un^2). Nous souhaitons montrer que Vn est une suite géométrique de raison -1.
Nous commençons par exprimer Vn+1 en fonction de Vn. En utilisant la relation de récurrence de la suite de Fibonacci, nous obtenons Vn+1 = (Un+2 * Un - Un+1^2). Nous procédons ensuite à un développement et simplifions l'expression pour obtenir Vn+1 = -Vn. Cela prouve que Vn est une suite géométrique de raison -1.
En calculant V1, nous trouvons que Vn = (-1)^n. Ainsi, nous avons montré que pour tout n positif, (Un+1 * Un-1 - Un^2) = (-1)^n.
La deuxième partie consiste à montrer que deux termes consécutifs de la suite de Fibonacci sont premiers entre eux. Nous utilisons l'égalité précédente pour cela. Nous remarquons que cette égalité ressemble à une égalité de Bézout. En multipliant les deux côtés de l'égalité par (-1)^n, nous obtenons U(n+1) * U(n-1) - U(n)^2 = 1. En écrivant cette égalité sous la forme U(n-1) * U(n+1) + U(n) * Un = 1, nous avons trouvé les coefficients de Bézout montrant que U(n-1) et U(n+1) sont premiers entre eux.
Ensuite, nous montrons que pour tout n, U(m+n) = Um * Un+1 + Um-1 * Un. Nous utilisons une double récurrence pour démontrer cette propriété. En vérifiant les deux premiers termes de la récurrence, nous constatons que la propriété est vérifiée. Ensuite, nous supposons que la propriété est vraie pour PM et PM+1, et nous montrons qu'elle est également vraie pour PM+2. Finalement, en utilisant cette propriété, nous montrons que le PGCD de Um et Un est égal à U(PGCD(m,n)).
En conclusion, nous avons étudié la suite de Fibonacci et montré plusieurs propriétés intéressantes, telles que la relation géométrique entre les termes de la suite, la coprimalité des termes consécutifs et la relation entre le PGCD de deux termes et le PGCD de leurs indices.
Maths
Algèbre
MPSI/PCSI
algorithme d’Euclide
Dans cet exercice, on cherche d'abord les diviseurs communs de 390 et 525 en utilisant l'algorithme d'Euclide. On trouve que le PGCD de ces deux nombres est de 15, ce qui signifie que les diviseurs communs sont 1, 3 et 5.
Ensuite, on cherche le PGCD de (3^123 - 5) et 25. Nous démontrons que le PGCD est de 1, car si le PGCD était de 5 ou de 25, cela signifierait que 5 divise (3^123 - 5), ce qui est impossible car 3 est un nombre premier.
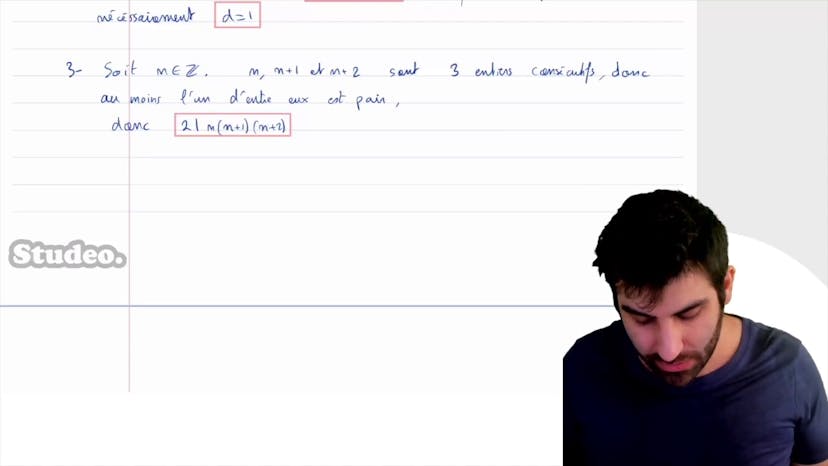
Enfin, on démontre que le produit de trois nombres entiers consécutifs est divisible par 6. En utilisant la propriété selon laquelle au moins l'un des trois nombres est pair et au moins l'un est divisible par 3 (car ils sont consécutifs), nous montrons que 2 et 3 divisent le produit. Puisque le PGCD de 2 et 3 est de 1, cela signifie que 6 divise le produit des trois nombres.
En résumé, on démontre que 15 est le PGCD de 390 et 525, que 1 est le PGCD de (3^123 - 5) et 25, et que 6 divise le produit de trois nombres consécutifs.
Maths
Algèbre
MPSI/PCSI

Equations de Bezou
Dans cet exercice, nous avons résolu quatre équations diophantiennes. Pour résoudre une équation diophantienne, nous commençons par trouver une solution particulière. Si cela n'est pas évident, nous utilisons une méthode spécifique pour garantir une solution. La solution générale se calcule en ajoutant ou soustrayant un coefficient devant l'autre inconnu.
Dans la première équation, le PGCD de 2 et 5 est 1. Nous trouvons facilement une solution particulière en prenant x = -1 et y = 1. La solution générale est alors écrite comme x = -1 - 5k et y = 1 + k.
Dans la deuxième équation, le PGCD est 17. Après simplification, nous obtenons 19x - 23y = 6. En appliquant l'algorithme de Clide, nous trouvons une solution particulière qui est x = -216 et y = -180. La solution générale est alors x = -216 + 23k et y = -180 + 19k.
Dans la troisième équation, le PGCD est 9. Après simplification, nous obtenons 18x + 23y = 3. En appliquant à nouveau l'algorithme de Clide, nous trouvons une solution particulière qui est x = 27 et y = -21. La solution générale est alors x = 27 + 23k et y = -21 + 18k.
Enfin, dans la dernière équation, le PGCD est 13 mais il ne divise pas 15, ce qui signifie qu'il n'y a pas de solution.
Maths
Algèbre
MPSI/PCSI

PGCD nombres pythagoriciens
Aucun résumé n'est disponible pour cette vidéo
Maths
Algèbre
MPSI/PCSI

Equation modulaire
Dans cet exercice, on cherche à trouver les solutions de l'équation AX congruent à B modulo N, avec des conditions sur A, B et N. On veut démontrer que cette équation a une solution si et seulement si le PGCD de A et N divise B.
Dans la première partie, on montre que si X est une solution de l'équation, alors le PGCD divise B. On utilise le fait que si AX est congruent à B modulo N, cela signifie que le PGCD de A et N divise B.
Dans la deuxième partie, on montre que si le PGCD divise B, alors l'équation a une solution. On utilise le théorème de Bézout pour montrer qu'il existe un nombre UV tel que AU + NV est égal à D. En multipliant cette équation par B, on obtient BAU + BNV = BD. En factorisant B par le PGCD, on obtient l'équation B'AU + B'NV = B. On en déduit que B'U est une solution de l'équation.
Dans la deuxième question, on suppose que le PGCD divise B et on pose N égale à DN'. On veut montrer que l'ensemble des solutions de l'équation est donné par X0 + QN', où Q est un entier. On utilise le fait que si X est une solution, alors A(X-X0) est congruent à 0 modulo N. En factorisant A par le PGCD, on obtient l'équation A'(X-X0) = KN'. Comme A' et N' sont premiers entre eux, on en déduit que N' divise X-X0. On peut alors montrer que tous les nombres de la forme X0 + QN' sont des solutions de l'équation.
Dans la troisième question, on cherche à montrer que deux solutions de l'équation sont congrues entre elles modulo N si et seulement si le PGCD divise la différence de leurs coefficients multiplicateurs. On en déduit que les solutions de l'équation sont de la forme X0 + QN', où Q est un entier et X0 est une solution particulière. On conclut que l'équation admet exactement ces solutions.
Maths
Algèbre
MPSI/PCSI

algorithme d’Euclide
Dans cet exercice, nous étudions les nombres A et B. A est composé de neuf fois le chiffre 1, et B est simplement la séquence des chiffres de 1 à 9. La première question demande de calculer le quotient et le reste de la division euclidienne de A par B. En effectuant cette division, nous trouvons que A est égal à 9 fois B plus 10, ce qui donne le quotient et le reste de la division.
Ensuite, nous devons trouver le PGCD (Plus Grand Commun Diviseur) de A et B. Pour cela, nous utilisons l'algorithme d'Euclide, que nous commençons en effectuant la division euclidienne de A par B. Ensuite, nous continuons l'algorithme en divisant le reste précédent (10) par 9, et ainsi de suite, jusqu'à ce que nous obtenions un reste nul ou égal à 1. Nous reconnaissons alors que le PGCD de A et B est égal à 1.
La dernière question consiste à déterminer deux antirelatifs UV tels que AU plus BV soit égal à 1. Pour ce faire, nous remontons l'algorithme d'Euclide en utilisant les résultats précédents. En développant les calculs, nous obtenons que 1 est égal à 111 111 112 fois B. Ainsi, nous trouvons les coefficients U et V qui vérifient la condition demandée.
Voilà pour le résumé SEO friendly de cet exercice.
Maths
Algèbre
MPSI/PCSI

Nombres de Fermat
Dans cet exercice, le but est de montrer que si M est un nombre entier positif tel que 2 puissance M plus 1 soit un nombre premier, alors M est une puissance de 2.
Pour cela, on développe une égalité : X puissance Q plus 1 est égal à X plus 1 fois X puissance Q moins 1, moins X puissance Q moins 2, plus X puissance Q moins 3, etc., jusqu'à plus 1.
Ensuite, en simplifiant cette équation, on remarque que si Q est impair, toutes les puissances paires de X ont un signe plus, ce qui fait apparaître le plus 1 nécessaire pour que 2 puissance M plus 1 soit premier.
Donc on peut conclure que M est une puissance de 2.
En utilisant cette propriété, on montre par l'absurde que si 2 puissance M plus 1 est premier et M n'est pas une puissance de 2, cela conduit à une contradiction.
Donc on en déduit que M est nécessairement une puissance de 2.
Maths
Algèbre
MPSI/PCSI

Nombres de Mersenne
Dans cette vidéo, on aborde le sujet des nombres de Mersenne.
Le premier objectif est de démontrer que si a^(n-1) est premier, alors a est égal à 2 et n est premier.
Pour cela, on factorise a^(n-1) avec a-1, a^(n-2), ..., jusqu'à 1. On remarque que 1-1 divise a^(n-1), tandis que a-1 est différent de a^(n-1) car n est supérieur ou égal à 2. Donc a-1 est égal à 1, ce qui implique que a est égal à 2.
Ensuite, il faut prouver que n est premier. On note n comme p*q, et on réécrit une égalité factorisée avec 2^(n-1). On observe que 2^(p-1) divise 2^(pq-1), qui est égal à 2^(n-1). Donc, si 2^(p-1) est égal à lui-même, cela signifie que p est égal à n. Ainsi, q est égal à 1 dans cette factorisation. De plus, si 2^(p-1) est égal à 1, cela entraîne que p est égal à 1. Donc, q est égal à n. Ainsi, dans tous les cas, n est un nombre premier.
Ensuite, on doit vérifier que M11 n'est pas premier. On calcule M11, qui est égal à 2^11 - 1, soit 2047. On peut le décomposer en 23 fois 89, ce qui prouve que ce n'est pas un nombre premier.
Le but de cette question est de comprendre pourquoi on nous l'a posée. On a vu précédemment que si un nombre de Mersenne est premier, alors la puissance n est aussi premier. Cependant, on vient de prouver le contre-exemple que si n est premier, alors 2^11 - 1 n'est pas premier. Donc, on a démontré que la réciproque ne marche pas.
Maths
Algèbre
MPSI/PCSI
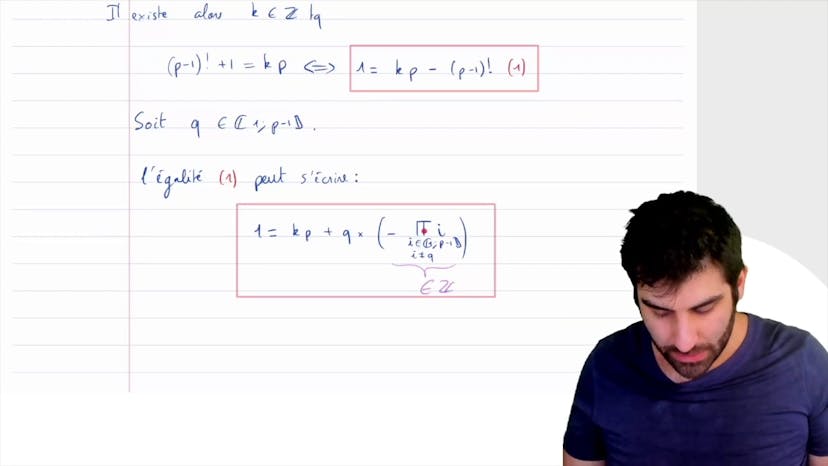
Théorème de Wilson
Dans cet exercice, nous allons démontrer que si P est un entier supérieur ou égal à 2 et que P-1! est congruent à -1 modulo P, alors P est premier. Nous allons démontrer cette implication dans un sens pour l'instant.
Nous partons donc du constat que P-1! est congruent à -1 modulo P, ce qui signifie qu'il existe un entier k tel que P-1! + 1 = k * P. En réarrangeant cette équation, nous obtenons 1 = k * P - (P-1!), que nous nommons équation 1 pour référence ultérieure.
Notre méthode pour prouver que P est premier consiste à montrer que P est premier avec tous les nombres plus petits que lui. Si tel est le cas, alors P est effectivement un nombre premier.
Nous prenons donc un nombre Q plus petit que P et dans l'intervalle [1, P-1!]. En réécrivant l'équation 1 comme 1 = k * P + Q * (P-1!), nous remarquons que le produit des entiers i dans l'intervalle [1, P-1!] (à l'exception de Q) est égal à P-1!. Nous avons également le terme -1.
Ce produit est un entier relatif, plus précisément un entier négatif, ce qui n'est pas important pour notre démonstration. Ce qui est important, c'est qu'il s'agit d'un entier. Nous pouvons donc considérer cette équation comme une équation de Bézout, où k * P et Q * (P-1!) sont premiers entre eux, selon le théorème de Bézout.
Ainsi, en prenant Q de manière arbitraire, nous avons démontré que P est premier avec tous les entiers plus petits que lui. Par conséquent, P est nécessairement un nombre premier.
Ceci conclut notre exercice.


