Cours d'apprentissage en ligne

Satellites sur la même orbite

Aujourd'hui, nous allons faire un exercice sur deux satellites sur la même orbite. L'idée de cet exercice est de déterminer quand le satellite B pourra rattraper le satellite A. Pour cela, le satellite B doit passer d'une orbite circulaire à une trajectoire elliptique. Dans un premier temps, nous montrons que la vitesse des satellites est constante sur une orbite circulaire grâce à la force gravitationnelle de la Terre. En utilisant les coordonnées polaires, nous obtenons les équations de la vitesse. Nous pouvons alors déterminer la vitesse V1, qui est la première vitesse cosmique, et la période du mouvement. Ensuite, nous étudions le changement d'orbite qui ne peut se faire qu'à l'apogée ou au périgée de l'ellipse. En effet, la vitesse est orthogonale à R sur une ellipse, ce qui signifie que le changement d'orbite ne peut se produire qu'à ces points spécifiques. Nous voulons également que le satellite B rattrape le satellite A après un seul parcours de l'ellipse. Pour cela, nous devons trouver le lien entre les vitesses V2 et V1 et l'angle α. En utilisant les lois de Kepler pour les ellipses, nous pouvons exprimer la période en fonction des autres grandeurs. En comparant les temps mis par les satellites A et B pour revenir à leur position initiale, nous obtenons une équation reliant V2, V1 et α. En utilisant l'énergie mécanique constante sur l'ellipse, nous pouvons éliminer un paramètre et obtenir une expression de V2 en fonction de V1 et α. Il est important de noter que la racine carrée doit être prise uniquement si l'argument est positif, ce qui limite α à être inférieur à 234°. En conclusion, cet exercice nécessite des calculs et une compréhension des concepts d'énergie mécanique et des mouvements elliptiques.

Second principe : cours

Le second principe de la thermodynamique stipule que la variation d'entropie d'un système est la somme de l'entropie créée et de l'entropie échangée. L'entropie mesure le désordre d'un système, et elle a tendance à augmenter dans l'univers. L'entropie créée ne peut pas être enlevée, tandis que l'entropie échangée peut être reçue ou cédée par les systèmes. La formule de l'entropie échangée est Q/Text, où Q est le transfert thermique entre deux systèmes et Text est la température extérieure. Le second principe stipule que l'entropie ne peut être créée que lors de transformations irréversibles où seul l'échange d'entropie a lieu. Cependant, il peut y avoir d'autres difficultés physiques liées au second principe. Dans les prochaines vidéos, nous examinerons les lois importantes découlant du second principe.

Variation d'entropie pour gaz parfait

Aujourd'hui, nous allons étudier la variation d'entropie pour un gaz parfait. La première identité thermodynamique est une formule essentielle pour calculer cette variation. Elle relie les différentiels des différentes grandeurs thermodynamiques telles que U, S, T, P et V. Nous pouvons isoler le terme DS dans cette formule en écrivant DS = DU/T + PDV/T. Comme nous savons que la variation d'énergie interne (DU) dépend uniquement de la température (T), nous pouvons la remplacer par CVDT/T, où CV est la chaleur spécifique à volume constant. Nous pouvons simplement intégrer la température entre la température initiale et la température finale. Le terme restant dans cette formule contient les variables P, V et T. Pour simplifier l'intégrale, nous pouvons utiliser la loi des gaz parfaits (PV = NRT), ce qui nous donne P/T = NR/V. Ainsi, nous avons seulement NRDV/V dans cette intégrale, ce qui correspond à une intégrale d'une seule variable. Finalement, nous intégrons cette formule pour passer de DS à delta S (variation de l'entropie). Comme S est une fonction d'état, nous pouvons utiliser le symbole delta. Ainsi, nous obtenons NCVM ln(TF/TI) + NR ln(VF/V), où NCVM est le produit du nombre de moles (N) et de la chaleur spécifique molaire à volume constant (CV), et TF, TI, VF et V sont les températures et volumes initiaux et finaux respectivement. Cette formule peut être écrite de différentes manières en fonction des grandeurs données dans l'exercice. Par exemple, on peut utiliser la masse molaire pour exprimer la variation d'entropie de manière massique, ou substituer CV par CP (chaleur spécifique à pression constante). Notez également qu'il est possible de conserver d'autres grandeurs thermodynamiques dans la formule, telles que la pression (P). Ainsi, la variation d'entropie peut être exprimée en fonction d'autres paires de grandeurs, telles que TV ou TP. En résumé, il est important de connaître la première identité thermodynamique pour calculer la variation d'entropie d'un gaz parfait. Cette formule peut être adaptée en fonction des grandeurs disponibles dans l'exercice, mais il est recommandé de la réduire à une forme plus simple avant d'effectuer les calculs.

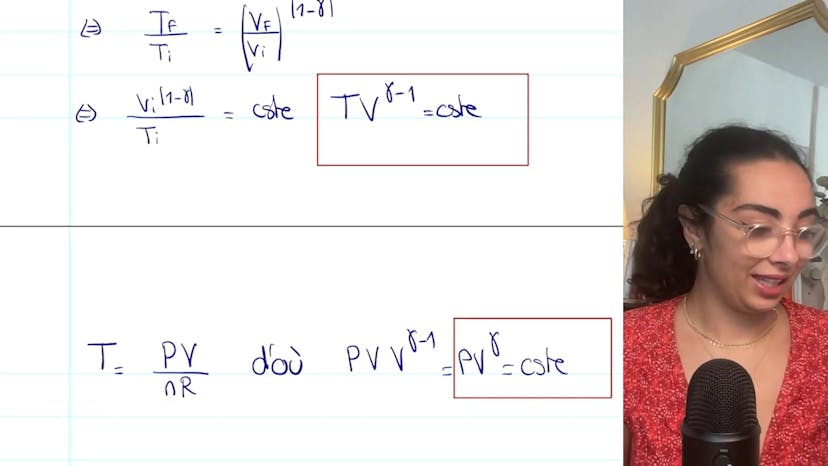
Lois de laplace

Aujourd'hui, nous allons aborder les lois de la place, qui sont très utilisées en thermodynamique pour les gaz parfaits. Il est essentiel de connaître les hypothèses d'application de ces lois. En particulier, une transformation adiabatique et réversible est nécessaire. Dans ce contexte, nous pouvons utiliser la variation d'enthalpie : delta S = NCVM LN(TF/TI) + NR LN(VF/VI) = 0. Cette équation peut également s'écrire sous la forme CVMLN(TF/TI) = -RLN(VF/VI). En utilisant la relation entre CP, CV et gamma (CP/CV = gamma), nous pouvons réarranger l'équation et obtenir ln(TF/TI) = -(gamma-1)ln(VF/VI). En simplifiant davantage, nous obtenons TF/TI = (VF/VI)^(1-gamma). Ainsi, nous pouvons écrire la loi de la place sous la forme TV^(gamma-1) = constante. Il est préférable de mémoriser la forme PV^(gamma) = constante de cette loi. Si nous voulons appliquer cette loi en fonction de T et V, nous pouvons utiliser la loi des gaz parfaits pour passer de P à T. Cela permet de simplifier l'équation et de garder en tête la relation PV^(gamma) = constante. Pour passer de la forme démontrée précédemment à PV^(gamma) = constante, nous utilisons la relation T = PV/(NR), qui ne change pas grand-chose car NR est constant. Il est crucial de savoir démontrer la loi de la place et de comprendre ses hypothèses d'application. La forme simplifiée PV^(gamma) = constante est la plus couramment utilisée et doit être mémorisée.

Solides en contact

Dans cet exercice de thermodynamique, nous étudions deux solides en contact avec des capacités thermiques différentes, C1 et C2. Les solides ont des températures initiales Ti1 et Ti2 et sont placés dans un endroit isolé avec des parois calorifiques fugées. La température finale TF est recherchée. Pour trouver TF, nous utilisons le fait que le système est isolé, ce qui signifie que la variation d'énergie interne ΔU est nulle. En utilisant l'expression de l'énergie interne en fonction de la capacité thermique et de la variation de température, nous obtenons une équation pour TF. Ensuite, nous étudions la variation d'entropie du système global. En utilisant le fait que l'entropie est une fonction d'état extensive, nous pouvons la décomposer en la somme des variations d'entropie des deux systèmes solides. En se basant sur la relation ΔS = Cln(TF/TI) pour une phase condensée pure, nous obtenons une expression pour la variation d'entropie totale ΔS. En conclusion, pour trouver les températures finales et les variations d'entropie dans ce type de problème thermodynamique, il est important d'utiliser le premier principe et de prendre en compte les propriétés des systèmes isolés et des phases condensées pures.

Gaz dans une enceinte

Bonjour à tous ! Aujourd'hui, nous allons étudier un exercice sur le second principe de la thermodynamique concernant un gaz dans une enceinte. Dans cet exercice, nous avons une enceinte indéformable avec des parois calorifugées, séparée en deux compartiments par une cloison d'air étanche, diatherme et mobile. Chaque compartiment contient le même gaz parfait. Au départ, le gaz du premier compartiment est à une température T0, une pression P0 et un volume V0, tandis que celui du deuxième compartiment a une pression deux fois plus grande, soit 2P0, avec les mêmes température T0 et volume V0. On laisse ensuite la cloison bouger librement jusqu'à atteindre l'équilibre. Pour déterminer l'état final, nous utilisons le premier principe de la thermodynamique. Comme l'enceinte est indéformable et calorifugée, la variation d'énergie interne est nulle. Nous avons donc Tf = T0, la température ne change pas. En utilisant la loi des gaz parfaits, nous calculons les pressions finales des compartiments : P1 = nRT0/V1 et P2 = nRT0/V2, avec V1 et V2 étant respectivement les volumes finaux des compartiments. Nous utilisons ensuite les deux équations de conservation du volume total de l'enceinte (2V0) et de la relation entre V1 et V2 (V2 = 2V1) pour trouver les valeurs des volumes V1 et V2. Finalement, en insérant ces valeurs dans les équations de pression, nous obtenons la pression finale P = 3n0RT0/2V0. Pour calculer la variation d'entropie, nous utilisons la formule ΔS = nCVM ln(TF/TI) + nR ln(VF/VI). Comme la transformation est isotherme, nous avons TF = TI. Ainsi, la variation d'entropie devient ΔS = nR ln(V1/V0) + 2n0R ln(V2/V0). En utilisant les valeurs des volumes déterminées précédemment, nous trouvons ΔS = n0R ln(32/27), qui est positif puisque 32 est supérieur à 27. En conclusion, pour déterminer l'état final, nous utilisons le premier principe et les lois des gaz parfaits. Pour calculer la variation d'entropie, nous utilisons le second principe et les formules de variation d'entropie.

Effet Joule

Dans cette vidéo, nous étudions un exercice de thermodynamique sur les échanges d'énergie. Nous avons un système composé d'eau et d'une résistance électrique. Nous voulons déterminer la variation d'entropie du système et l'entropie créée. Nous commençons par utiliser le deuxième principe de la thermodynamique pour trouver les variations d'entropie. Nous utilisons une formule pour la variation d'entropie d'une phase condensée pure, qui s'applique à la fois à l'eau et à la résistance. Comme la température est constante, la variation d'entropie totale est nulle. Ensuite, nous séparons la variation d'entropie en deux parties : celle échangée par le système et celle créée. Nous pouvons déterminer facilement l'entropie échangée en utilisant la formule de transfert thermique. Nous trouvons un résultat négatif, ce qui signifie que l'entropie échangée est décroissante. Pour l'entropie créée, nous utilisons à nouveau la formule de la variation d'entropie. Nous trouvons un résultat positif, ce qui est conforme au deuxième principe de la thermodynamique. Nous commentons également le signe de l'entropie créée en expliquant que toutes les grandeurs impliquées sont positives, y compris la résistance et la température. Nous passons ensuite à un autre cas où le système est isolé thermiquement, ce qui signifie qu'il n'y a aucun transfert thermique avec l'extérieur. Dans ce cas, la variation d'enthalpie est nulle, et la variation d'énergie est égale à l'énergie électrique dissipée par la résistance. Nous trouvons une variation positive d'entropie, ce qui est toujours conforme au deuxième principe de la thermodynamique. En résumé, dans cet exercice, nous avons utilisé les formules de la thermodynamique pour calculer les variations d'entropie d'un système composé d'eau et d'une résistance électrique. Nous avons discuté du signe de l'entropie créée en relation avec les grandeurs physiques impliquées. Nous avons également noté l'importance de manipuler correctement les formules d'entropie et de tenir compte des conditions du système pour obtenir les résultats finaux.

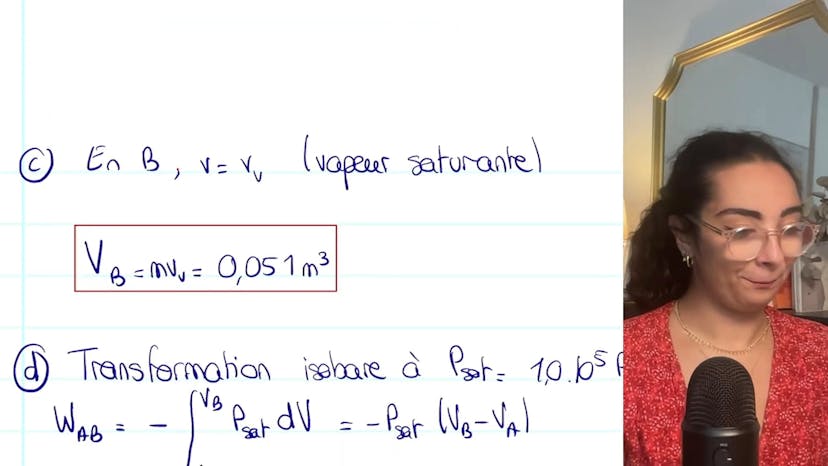
Mélange liquide-vapeur

Dans cette vidéo, nous abordons le sujet de la vaporisation d'un mélange liquide-vapeur. Nous commençons par tracer le diagramme de Clapeyron, qui représente la pression en fonction du volume massique. Nous observons une forme de cloche caractéristique, où en-dessous de la courbe se trouve le mélange liquide-vapeur. Nous plaçons ensuite les points VL (liquide saturant) et VV (vapeur saturante) sur le diagramme. Ensuite, nous plaçons le point A qui correspond à un titre en vapeur de 80%. Nous utilisons le théorème des moments pour trouver le volume massique VA du mélange, ainsi que le volume total correspondant. Nous introduisons ensuite le point B, où une vaporisation isobare totale se produit jusqu'à atteindre la vapeur saturante. Nous déduisons que VB est égal à M fois VV. Enfin, nous déterminons les expressions de WAB (travail échangé) et de QAB (chaleur échangée). La transformation étant isobare, le travail s'obtient en utilisant la formule WAB = Psat * (VB - VA). Nous trouvons que WAB est égal à -1 kJ. Pour la chaleur échangée, nous utilisons la relation QAB = ΔHAB pour une transformation monobare. Nous calculons que QAB est égal à 14 kJ. En conclusion, il est important de bien comprendre le diagramme de Clapeyron pour réussir cet exercice. Le théorème des moments est également utile pour les phases liquide et vapeur. Appliquer le premier principe permet de trouver les valeurs de WAB et QAB.

Fonte de glace

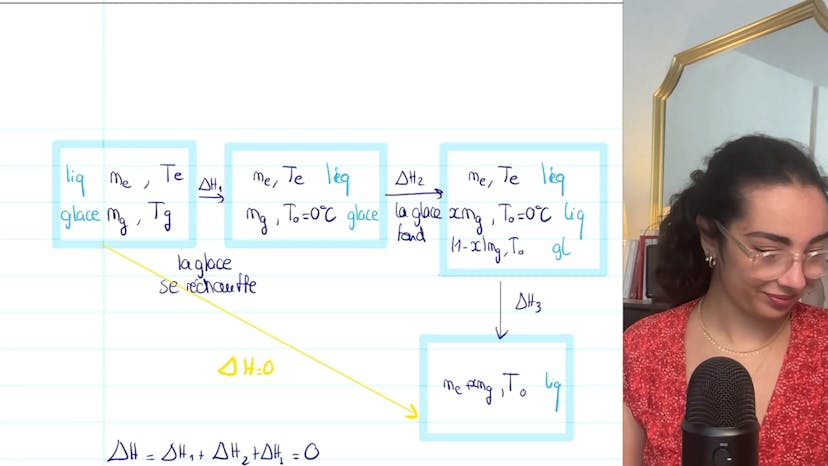
Bonjour à tous, dans cet exercice de thermodynamique, nous étudions la fonte d'un glaçon. Nous calculons l'état final du système et la variation d'entropie. Nous supposons que l'on mélange une masse d'eau liquide à la température TE et une masse de glace à la température TG dans une enceinte calorifugée à pression atmosphérique. Nous connaissons les capacités thermiques massiques de l'eau et de la glace, ainsi que les enthalpies de fusion de la glace et la chaleur latente. Nous devons déterminer l'état final du système. Nous faisons l'hypothèse d'un mélange eau-glace à 0°C. Nous envisageons également d'autres possibilités : que toute la glace ait fondu ou que tout le liquide se soit solidifié. Nous utilisons le premier principe de la thermodynamique pour décomposer les étapes et calculer ΔH. En utilisant la conservation de l'énergie, nous trouvons une fraction massique de 2,4% de glace fondue. Pour la variation d'entropie du système, nous décomposons également les étapes et calculons ΔS. Nous obtenons une variation d'entropie totale de 1,9 J/K. Il est important de noter que nous devons faire des hypothèses, vérifier leur cohérence et être prêt à ajuster nos calculs si nécessaire. En conclusion, retenez l'importance de décomposer les étapes dans ce type d'exercice et de réfléchir aux différentes possibilités.

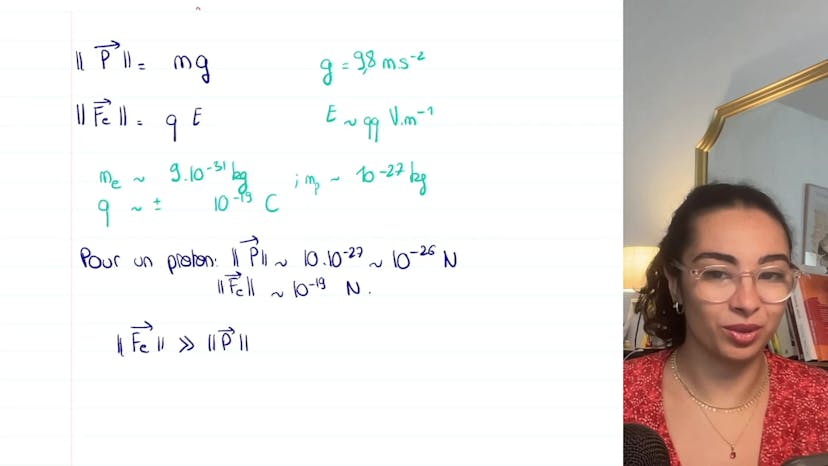
Poid et force électrique

Dans cet exercice, l'objectif est de comprendre pourquoi nous pouvons négliger le poids dans les problèmes impliquant des particules chargées. Pour cela, nous comparons l'ordre de grandeur du poids à celui de la force électrique. Le poids est déterminé par la formule m fois g, où m est la masse de la particule et g est l'accélération due à la pesanteur (environ 9,8 m/s²). La force électrique, quant à elle, est calculée en multipliant la charge électrique de la particule (q) par le champ électrique (E). En prenant des ordres de grandeur typiques, le champ électrique est d'environ quelques volts par mètre. Les paramètres importants sont la masse des particules - pour un électron environ 9 x 10-31 kg et pour un proton environ 9 x 10-27 kg - ainsi que la charge électrique qui est d'environ 10-19 coulombs. En se concentrant uniquement sur les normes des forces, on néglige les unités. Donc, en termes de poids, le proton a la masse la plus grande et donc le poids le plus élevé, qui est d'environ 10-26 newtons. Pour la force électrique, elle est d'environ 10-19 newtons, ce qui est beaucoup plus élevé que le poids. Il y a donc sept ordres de grandeur entre la force électrique et le poids. Comme le champ électrique peut être beaucoup plus élevé que quelques volts par mètre, la force électrique est bien plus grande que le poids. C'est pourquoi, dans les problèmes impliquant des particules chargées dans des champs électromagnétiques, nous négligeons le poids.

Électrode

Aujourd'hui, nous allons parler des électrodes et faire un exercice pratique sur le sujet. Les électrodes que nous avons sont planes, parallèles et soumises à une tension U positive. Tout d'abord, nous devons déterminer comment orienter le champ électrique dans ce dispositif. Pour ce faire, nous savons que le champ électrique descend les potentiels. En utilisant la formule E = -∇V, qui lie le champ électrique au potentiel, nous pouvons voir que si la tension U va dans une certaine direction, le champ électrique va dans la direction inverse. Ainsi, E = -U/D, si le champ est uniforme. Ensuite, nous devons calculer la vitesse à laquelle un proton atteindra l'autre électrode, en partant de l'électrode Z = 0. Pour cela, nous allons raisonner en termes de potentiel, qui est essentiellement une forme d'énergie potentielle. En utilisant le théorème énergétique, nous pouvons établir que le potentiel en Z = 0 est QU, où Q est la charge du proton. Le potentiel en D est nul, car c'est le point de référence où le potentiel est considéré comme étant nul. En utilisant le théorème de l'énergie mécanique, nous pouvons équilibrer l'énergie potentielle en Z = 0 (QU) avec l'énergie cinétique en D (1.5mv², où m est la masse du proton et v est sa vitesse). En résolvant cette équation, nous obtenons que la vitesse v est égale à la racine carrée de (2QU/m). Cette formule est souvent utilisée dans les problèmes d'accélération pour calculer la vitesse obtenue en appliquant une différence de potentiel entre deux points. En résumé, dans cet exercice sur les électrodes planes et parallèles soumises à une tension positive, nous avons déterminé l'orientation du champ électrique et calculé la vitesse à laquelle un proton atteint l'autre électrode à partir de l'électrode Z = 0. La vitesse est donnée par la formule racine de (2QU/m).