 Tous les sujets
Tous les sujets Maths
Maths Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée Prépa Examens
Prépa Examens
Terminale
Première
Seconde
MPSI/PCSI
2BAC SM Maroc
 Tous les sujets
Tous les sujets Maths
Maths Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée Prépa Examens
Prépa Examens
Maths Spé
Analyse
Terminale

Double racine
Bonjour à tous ! Aujourd'hui, je vais vous résumer ce cours sur les limites de manière SEO friendly. Dans cet exercice de difficulté intermédiaire, nous devons étudier les limites. Tout d'abord, nous devons montrer que la fonction f est définie sur l'ensemble des réels. Pour cela, nous devons vérifier que les racines de la fonction sont positives ou nulles. Ensuite, nous devons étudier le tableau de variation de la fonction f. Pour pouvoir le faire, nous devons justifier la dérivabilité de f sur l'ensemble des réels. Puis, nous devons calculer la dérivée de la fonction f en utilisant la composition. Nous constatons que la dérivée est toujours positive, ce qui signifie que la fonction est strictement croissante. Enfin, nous devons étudier les limites de la fonction f. En utilisant la composition, nous montrons que la limite de f tend vers l'infini lorsque x tend vers l'infini et que la limite de f tend vers zéro lorsque x tend vers moins l'infini. Pour conclure, nous pouvons tracer le graphe de la fonction f en utilisant des valeurs remarquables. Voilà pour ce résumé SEO friendly de ce cours sur les limites. Merci d'avoir suivi !
Maths Spé
Analyse
Terminale
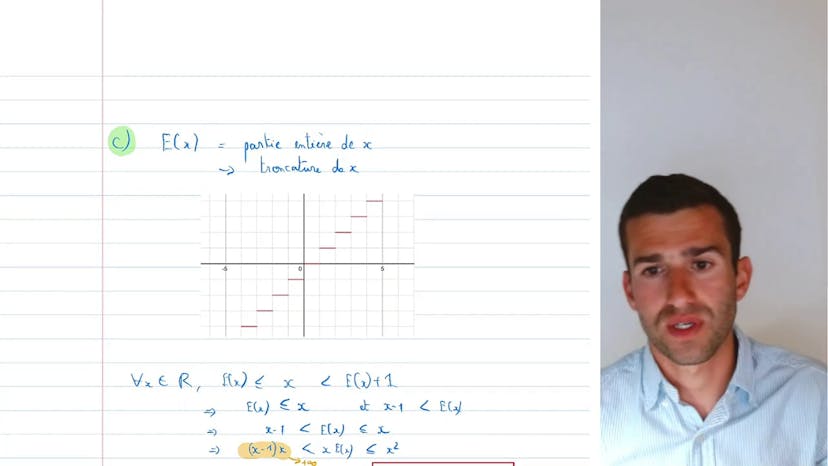
Calculs de limites complexes
Dans cette vidéo, le professeur explique comment résoudre cinq exemples de limites mathématiques complexes, destinées aux étudiants de niveau terminale++ et de préparation. Le premier exemple implique des racines et l'utilisation de quantités conjuguées pour simplifier l'expression, avec une astuce consistant à factoriser par le terme de plus haut degré. Le deuxième exemple implique des taux d'accroissement et la dérivée pour résoudre l'expression indéterminée, tandis que le troisième exemple utilise la partie entière pour encadrer l'expression afin de résoudre la limite. Le quatrième exemple utilise de nombreuses racines et une quantité conjuguée pour simplifier l'expression, tandis que le cinquième exemple divise l'expression en deux parties et utilise les taux d'accroissement pour résoudre l'expression indéterminée, en trouvant les limites des deux parties séparément.
Maths Spé
Analyse
Terminale

Intro Suites et limites
Lors de cette vidéo sur les limites de suite, le professeur explique que les définitions formelles peuvent paraître moches et effrayantes, mais qu'elles sont nécessaires pour obtenir des prédictions précises. Il suggère de toujours se référer aux dessins qui accompagnent les formules, pour mieux les comprendre. À cet égard, les limites de suite ont des similitudes avec l'étude des dérivées, où les tables de dérivées classiques ont remplacé les calculs fastidieux de taux d'accroissement. Dans le cas des limites de suite, il y a des tableaux de limites classiques à connaître par cœur. Le cours est divisé en trois parties principales: la définition des limites en infini, en moins infini, et en un point L réel, la présentation des limites de référence et des opérations sur les limites, et enfin une section bonus sur les limites des suites géométriques. Les principales méthodes d'étude incluent l'application de la définition formelle dans les exercices, l'utilisation des limites de référence et des opérations pour prédire les limites, la résolution de cas plus compliqués, et un rappel sur la somme des termes d'une suite géométrique.
Maths Spé
Analyse
Terminale

Intro Convergence
Les théorèmes de convergence sont utilisés pour analyser des suites mathématiques complexes qui peuvent sembler difficiles à comprendre. Les deux théorèmes principaux sont le théorème de comparaison et le théorème de gendarme, qui ont des applications spécifiques pour montrer que les suites convergent ou divergent. Les suites minorées, majorées et bornées sont également définies, ce qui conduit au théorème de convergence monotone, important pour les mathématiques de niveau avancé. Les méthodes comprennent la gestion de sinus de n, de moins-un puissance n, et les suites homographiques, qui tombent souvent dans les examens.
Maths Spé
Analyse
Terminale

Récurrence et croissance
La démonstration par récurrence est une méthode importante à maîtriser en mathématiques. Pour prouver l'hérédité de la suite, qui est la partie la plus compliquée de cette démonstration, voici quelques astuces. Pour démontrer que la suite est strictement décroissante, on définit la propriété P2n, qui est vraie pour tout n. Pour l'initialisation, on commence par u0 et pour l'hérédité, on écrit l'hypothèse de récurrence et ce qu'on veut montrer, en veillant à être explicite. Pour montrer que un+2 est plus petit que un+1, on utilise l'hypothèse de récurrence en la composant avec une fonction affine f, qui est strictement croissante. Enfin, on montre l'hérédité rigoureusement. Il est important de ne pas confondre la valeur de la suite au rang n avec l'objet suite elle-même, en utilisant des parenthèses pour éviter toute ambiguïté.
Maths Spé
Analyse
Terminale

Conjecture puis récurrence
Dans ce cours, on utilise la démonstration par récurrence pour calculer la somme des entiers de 1 à n, qui est égale à n*(n+1)/2. Il est important de connaître le résultat que l'on veut démontrer avant d'utiliser cette méthode. On pose la proposition P2n selon laquelle la somme des entiers naturels jusqu'à n est égale à n*(n+1)/2. On vérifie ensuite la propriété pour n=1, puis on utilise l'hypothèse de récurrence pour montrer que P2n+1 est aussi vrai. En factorisant par n+1, on démontre que pour tout n antinaturel non nul, la somme des entiers de 1 à n est égale à n*(n+1)/2.
Maths Spé
Analyse
Terminale

Hérédité : comment démarrer ?
Dans ce cours de mathématiques, on nous montre comment utiliser la méthode de récurrence pour démontrer l'hérédité. Pour cela, on utilise deux cas possibles : soit on part de l'hypothèse de récurrence, soit on part de la propriété au rang Un+1. Ces deux méthodes sont possibles et il n'y a pas de méthode meilleure, tout dépend de l'exercice. Il est également important de faire le lien entre l'hypothèse de récurrence et ce que l'on veut démontrer. En utilisant un exemple simple, on montre que la méthode de récurrence permet de prouver que pour tout n, Un est strictement positif.
Maths Spé
Analyse
Terminale

Limite avec A ou Ɛ
Dans ce cours, on explique la définition mathématique d'une limite en mathématiques. L'objectif est de trouver le plus petit entier n0 tel que, pour toutes les valeurs de la suite au-delà de ce rang, elles soient supérieures à un certain réel a. Cela signifie que même si le réel a est très grand, il existe un rang à partir duquel toutes les valeurs de la suite seront supérieures à a. Pour trouver n0, on résout une équation et utilise la partie entière du résultat pour s'assurer que n0 est un nombre entier. La définition complète de la limite est illustrée par un exemple de suite qui tend vers l'infini. Bien que les définitions formelles puissent sembler difficiles, elles sont importantes pour comprendre les limites en mathématiques.
Maths Spé
Analyse
Terminale

Forme indéterminée 1 : factoriser par terme de plus haut degré
Dans ce cours, nous allons étudier les méthodes pour calculer des limites indéterminées. Nous commençons avec le cas des polynômes en n, où le terme de plus haut degré est le seul à compter. Nous le démontrons en factorisant par le terme de plus haut degré et en observant le comportement de la fraction obtenue. Si nous avons un terme de plus l'infini fois un coefficient, nous obtenons une limite qui tend vers plus l'infini. Ainsi, la factorisation par le terme de plus haut degré nous permet de déterminer le coefficient dominant qui va imposer la limite. Cette méthode fonctionne pour tous les polynômes.
Maths Spé
Analyse
Terminale

Forme indéterminée 2 : la quantité conjuguée
Ce cours aborde les méthodes pour une fonction rationnelle, qui est un polynôme divisé par un autre polynôme. Pour résoudre la fonction, il faut factoriser par le terme de plus haut degré pour trouver quel terme l'emporte. Il y a trois cas de figure : lorsque le degré de P est strictement supérieur à celui de Q, lorsque le degré de Q est strictement supérieur à celui de P, ou lorsque les deux sont de la même force. Dans ce dernier cas, la limite tend vers le rapport des coefficients dominants de P et Q. Les n se simplifient en partie et l'on peut trouver la solution optimale pour la fonction.
Maths Spé
Analyse
Terminale

Limite d'une somme géométrique
En bref, pour calculer une somme limitée, il faut d'abord vérifier si les termes de la somme correspondent à une suite arithmétique ou géométrique connue. Si c'est le cas, on peut utiliser une formule adaptée pour calculer la somme. Dans cet exemple, les termes correspondent à une suite géométrique, ce qui permet d'appliquer la formule de la somme des termes consécutifs d'une suite géométrique. Après quelques vérifications, on trouve que la somme tend vers l'infini.
Maths Spé
Analyse
Terminale

Trouver à la calculette "le plus petit entier tel que..."
Dans ce cours, nous étudions une suite en cherchant le plus petit entier tel que le terme de la suite soit supérieur à une certaine valeur. La suite a0=2 et la relation de récurrence est an+1=3an. Nous voyons que la suite augmente très vite. Nous utilisons ensuite un petit programme pour trouver le premier entier n tel que an>1000. Le programme utilise une boucle "tant que" pour calculer les termes de la suite jusqu'à ce que celui-ci dépasse 1000. Nous affichons ensuite la valeur de n pour connaître à quel rang nous sommes. Nous pouvons également calculer cela par itération sans programme. Le premier entier n tel que an>1000 est 6. Cette méthode peut être utile pour résoudre d'autres problèmes similaires.


