Cours d'apprentissage en ligne

Décharge de deux condensateurs

Dans cette vidéo, Matisse de Studio étudie la décharge de deux condensateurs en série. Il résout une équation différentielle en utilisant la loi des mailles et la relation courant-tension du condensateur. Il détermine également la variation d'énergie du système constitué par la résistance et les condensateurs. Il démontre que l'énergie dissipée par effet Joule dans la résistance est égale à la valeur absolue de la variation d'énergie du système total. Enfin, il explique comment ce phénomène décrit concrètement ce qui se passe à l'intérieur d'un système électrique.

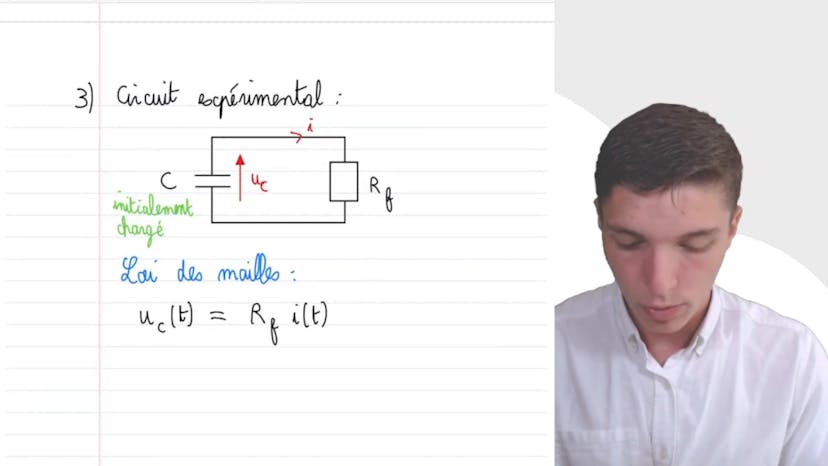
Résistance de fuite

Dans cette vidéo, on étudie la modélisation d'une résistance de fuite d'un condensateur après avoir observé expérimentalement la décharge spontanée d'un condensateur de capacité 100 pF initialement chargé sous une tension de 10V. On explique que cette décharge est causée par le phénomène de fuite, où les électrons qui se trouvent sur une des plaques du condensateur peuvent passer à travers l'isolant qui sépare les deux plaques. On modélise ce phénomène en ajoutant une résistance en parallèle avec le condensateur. Pour calculer l'ordre de grandeur de la résistance de fuite, on propose un circuit comprenant un condensateur initialement chargé et une résistance de fuite en série, et on pose une équation différentielle pour la tension du condensateur en régime permanent. En résolvant cette équation différentielle et en utilisant les données expérimentales, on isole la résistance de fuite, qui est finalement égale à 0.5 MHz. Cette résistance est très importante car elle permet au condensateur de retenir les charges passées.

Encore un RLC

Dans cette vidéo, nous étudions un circuit RLC avec un condensateur en dérivation. Nous établissons l'équation différentielle vérifiée par le courant I en utilisant la loi des mailles. Ensuite, nous identifions la pulsation propre ω0 et le facteur de qualité Q, qui décrit la qualité de l'oscillateur considéré. Nous expliquons également qualitativement l'expression du facteur de qualité. Nous résolvons finalement l'équation différentielle et donnons l'expression de I de T ainsi que son allure. Nous soulignons l'importance de savoir adapter notre raisonnement face à des situations inhabituelles.

Filtre de Wien

Dans cette vidéo, Matisse de Studio explique le filtre de Wien qui est un montage composé de deux résistances identiques, deux condensateurs de capacité identique mis en série et deux autres en parallèle. Il montre comment écrire l'équation différentielle en utilisant la loi des mailles et la relation courant-tension. Il détermine également les conditions initiales portant sur V et dV. Matisse explique que le filtre de Wien sera étudié en détails dans le chapitre suivant sur le filtrage linéaire.

RLC parallèle

Dans cette vidéo, Matisse de Studio étudie un circuit RLC en parallèle. Les conditions initiales sont données. On établit l'équation différentielle liée à U2D dans le circuit. En normalisant l'équation différentielle, on obtient D2U sur DT2 + 1/RC DU sur DT + 1/LC U de T = 0. On met ensuite cette équation sous forme canonique et on donne l'expression de la pulsation propre et du facteur de qualité en fonction des différents dipôles. On justifie ensuite qu'à l'instant T = 0, I de L et U sont égaux à 0. On résout ensuite l'équation différentielle pour déterminer la dérivée temporelle et la constante A. Enfin, on trace l'allure de U de T. Il s'agit d'un régime impériodique qui tend vers 0 avec une pente à l'origine de Éta sur C.

RLC série

Bonjour à tous, dans cette vidéo nous allons étudier un circuit RLC série. Plus précisément, nous étudions le circuit 6 contre où le condensateur est initialement chargé (UC en T égale 0 égale U0). Nous devons déterminer les valeurs de I, UC et UL à la fermeture du circuit en T égale 0+ et en régime permanent. Nous commençons par UC en 0+. Par continuité du courant de la tension, UC en 0+ est égal à UC en 0-, donc U0. En ce qui concerne I en 0+, par continuité du courant traversant la bobine, car avant l'interrupteur était ouvert, I en 0+ est égal à I en 0-, donc 0. Pour déterminer UL, nous devons utiliser un schéma équivalent. En 0+, la tension aux bornes de la résistance est égale à 0 car le courant est nul. Par loi des mailles, on obtient que UL en 0+ est égal à U0. En régime permanent, UL et I sont faciles à déterminer. UL est égal à 0 car en régime permanent il n'y a plus de variation de tension. De même, I est égal à 0 car en régime permanent il n'y a plus de variation de courant. UC en régime permanent est également égal à 0 car la tension aux bornes de la résistance est nulle. Parmi ces grandeurs, Y représente le courant qui traverse le circuit. Pour le mesurer, on peut utiliser la loi d'Ohm en visualisant la tension aux bornes de la résistance à l'oscilloscope. On divise ensuite cette tension par R pour obtenir le courant. Nous devons résoudre l'équation différentielle pour I en fonction de ω0 et introduire le paramètre M qui vaut R sur 2L ω0. L'équation différentielle est D2I sur DT2 plus 2ω0M D sur DT plus 1 sur LCI de T est égal à 0. En résolvant cette équation, nous obtenons une solution en fonction de ω, qui vaut ω0 racine de 1 moins M². Pour mesurer ω, nous pouvons relever une pseudo-période sur le graphe. En utilisant cette valeur, nous pouvons calculer ω en utilisant la formule O est égal à 2π sur T2 moins T1. En continuant la résolution, nous obtenons une solution homogène pour I de T. Nous utilisons ensuite des approximations pour trouver une relation simple entre le rapport Y1 sur Y2 et M. Cette relation est environ égale à Mω0 Tp, avec Tp qui vaut T2 moins T1. Pour compenser l'amortissement, nous pouvons proposer de mettre en place un générateur de courant pour compenser la perte d'énergie due à l'effet Joule de la résistance. En conclusion, nous avons étudié en détail un circuit RLC série et appliqué nos connaissances en théorie sur le filtre RLC à un relevé expérimental. Merci et à bientôt !

Un oscillateur électrique

Dans cette vidéo, Matisse de Studio explique la filtration d'un signal non-harmonique en se basant sur sa représentation en série de Fourier et la transformation de Fourier en filtrage linéaire. Le signal d'entrée est un signal créneau de pulsation ω1 et d'amplitude A, dont la représentation temporelle est donnée. Une fonction de transfert harmonique F1 de jω qui est égale à 1 divisé par 1 plus jω divisé par ω1 sur 10 est utilisée pour filtrer le signal. Le spectre du signal d'entrée est représenté en multiples de ω1 impaires et l'amplitude est caractéristique d'un grain O. La fonction de transfert du filtre est représentée en diagramme de Bode en phase et correspond à un filtre passe-bas de fréquence de coupure ω1 sur 10. Ensuite, le signal de sortie est déterminé en appliquant la fonction de transfert à chaque sinus du signal d'entrée, avec un facteur de gain et de phase modifiant la fonction. Le signal de sortie est donc la somme des sinus modifiés. En résolvant l'équation, on obtient la formule finale pour le signal de sortie.

Circuit bouchon

Dans cette vidéo, nous étudions le circuit Bouchon, qui est constitué d'un dipôle avec une bobine et un condensateur montés en dérivation. Nous déterminons l'impédance complexe ZS d'un dipôle RLC série en fonction des composants, de R, de la pulsation propre et du facteur de qualité. Ensuite, nous exprimons l'impédance complexe Z du dipôle parallèle sous la forme R divisé par JCωZS, facteur de 1 plus JQω sur ω0. Nous montrons que lorsque le facteur de qualité est très élevé et la pulsation pas trop faible, l'impédance peut se mettre sous la forme approchée Z est environ égal à Q²R² sur ZS complexe. Nous déterminons également que le module de l'impédance complexe est maximal lorsque la pulsation est égale à la pulsation propre ω0, et que le circuit est alors bloqué, d'où l'appellation circuit bouchon. Enfin, nous déterminons les intensités réelles qui traversent respectivement le condensateur et la bobine en fonction de E0, Q et R, et constatons que le circuit est véritablement un circuit bouchon.

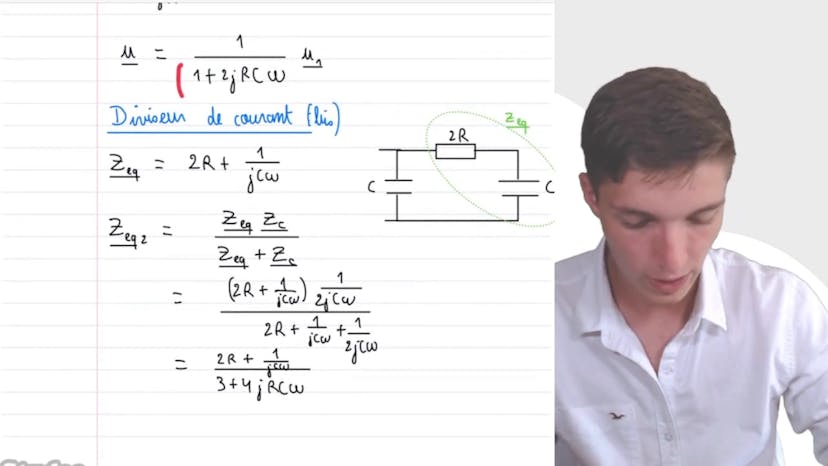
Equation différentielle via les complexes

Dans cette vidéo, Matisse de Studio explique comment établir une équation différentielle en utilisant les complexes. L'équation à déterminer est 4 tau² d2u sur dt2 plus 5 tau du sur dt plus U est égal à E. À l'aide d'un diviseur de tension, la tension U peut être exprimée en fonction d'une tension intermédiaire U1, qui peut ensuite être exprimée en fonction de la tension de départ E. En utilisant des manipulations de grandeurs complexes, Matisse détermine l'impédance équivalente et applique le diviseur de tension pour obtenir la relation entre U et E en complexe. En repassant ensuite en réel, l'équation différentielle est obtenue. Cette méthode démontre la puissance de la résolution à l'aide des complexes pour obtenir des résultats électro-signétiques de manière plus simple.

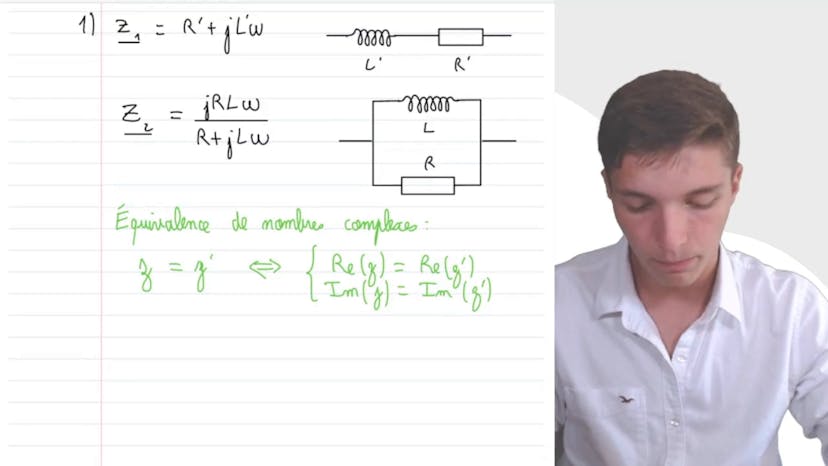
Equivalence entre deux dipôles

Dans cette vidéo, nous étudions l'équivalence entre deux dipôles complexes en régime sinusoidal forcé de pulsation oméga. Les dipôles sont constitués d'une bobine d'inductance L et d'une résistance R en série ou en parallèle. Pour être équivalents, les deux dipôles doivent avoir les mêmes impédances complexes. Pour cela, nous déterminons leurs impédances complexes en fonction de oméga. Ensuite, nous extrayons leurs parties réelles et imaginaires pour les comparer. Si nous remplaçons la bobine L par un condensateur C, nous obtenons une relation qui est impossible à satisfaire car la capacité serait strictement négative. En conclusion, nous travaillons avec des nombres complexes comme les autres pour déterminer l'équivalence des dipôles.

Filtre de Wien

Dans cette vidéo, Matisse de Studio nous parle du filtre de Wien. Il explique que ce filtre est utilisé dans les oscillateurs autant entretenus et qu'il est assez simple à réaliser. En analysant les comportements asymptotiques, il détermine que c'est un filtre passe-bas. Ensuite, il calcule la fonction de transfert du filtre en utilisant le diviseur de tension. Il obtient une expression satisfaisante en normalisant la fonction de transfert. Il introduit également les notions de ω0 et de X. Il écrit ensuite la fonction de transfert sous une forme canonique, avec H égal à H0 divisé par 1 plus JQ, où H0 est 1/3 et Q est 1/3. Matisse calcule ensuite le gain maximal du filtre, qui est égal à H0, soit 1/3. Il exprime également sa valeur en décibels, qui est d'environ -9,5 décibels. Il calcule également le déphasage correspondant, qui est de 0. En représentant le diagramme de Bode, il montre que le gain en décibels a une pente de +20 en 0 et -20 en infini, avec un maximum à la fréquence ω0. La phase varie de π/2 à -π/2. Ensuite, Matisse explique comment calculer la pulsation propre ω0 pour certaines valeurs et donne le signal de sortie du filtre si le signal d'entrée est E0+ E0cos(ωt) + E0cos(10ωt) + E0cos(100ωt). Il utilise la méthode de filtrage linéaire pour calculer le signal de sortie en appliquant la fonction de transfert aux différentes composantes du signal d'entrée. Il montre que la composante continue est coupée par le filtre, que la composante à ω0/10 a un gain de 1/10 et une phase de -1.2 radian, et que la composante à ω0 a un gain de 1/3 et pas de phase supplémentaire. Il montre également que la composante à 10ω0 a un gain de 1/10 et une phase de 1.2 radian. Finalement, il donne le signal de sortie, qui est la somme de toutes les composantes filtrées. En conclusion, le filtre de Wien est un filtre passe-bas utilisé dans les oscillateurs autant entretenus. Sa fonction de transfert est H = H0/(1 + JQ(X - 1/X)), avec H0 = 1/3 et Q = 1/3. Son gain maximal est de 1/3, ce qui correspond à environ -9,5 décibels, et son déphasage est de 0. Il permet de filtrer les différentes composantes d'un signal d'entrée pour obtenir un signal de sortie filtré.