 Tous les sujets
Tous les sujets Maths
Maths Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée Prépa Examens
Prépa Examens
Terminale
Première
Seconde
MPSI/PCSI
2BAC SM Maroc
 Tous les sujets
Tous les sujets Maths
Maths Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée Prépa Examens
Prépa Examens
Maths Spé
Analyse
Terminale

Équation y'=ay+φ
Dans ce cours, nous apprenons à résoudre une équation différentielle de la forme y = y + phi, où phi est une fonction qui n'est pas constante. Pour trouver la solution particulière, nous utilisons la méthode habituelle de trouver une solution particulière et de la sommer à l'équation homogène y = y. Cependant, nous ne cherchons pas une solution particulière sous une forme constante et avons besoin d'un petit indice pour la trouver. On nous demande ensuite de montrer que f est solution de E équivaut à f - p solution de E', où E' est l'équation sans le second ordre et f et p sont des fonctions. Nous isolons ensuite f pour trouver la solution de E. Nous remarquons que nous avons toujours la constante multiplicative inconnue, mais nous avons besoin de conditions particulières dans notre fonction pour la trouver.
Maths Spé
Analyse
Terminale
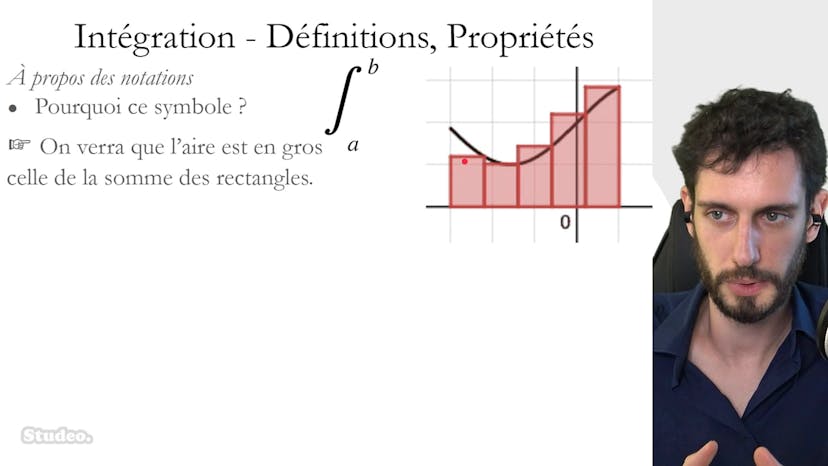
Introduction
Dans cette vidéo, le sujet principal est l'introduction au premier topic du chapitre sur les intégrales. On y présente les définitions et les propriétés, ainsi qu'une explication sur ce qu'est une intégrale. Le but est de calculer des valeurs sous des courbes. Le sous-chapitre consiste en la pose de bases pour des fonctions continues, positives et négatives. L'auteur explique comment trouver les r sous la courbe d'une fonction constante ou affine, ce qui permet de comprendre comment fonctionne l'intégrale sous une fonction plus complexe. Il explique également l'approximation utilisée pour trouver cette aire, basée sur la somme d'une infinité de rectangles de largeur delta x et de hauteur f de x en chaque point. Les points de cours abordés dans ce sous-chapitre concernent la définition de l'intégrale pour les fonctions continues positives et de signes quelconques, ainsi que les méthodes pour trouver et estimer l'intégrale.
Maths Spé
Analyse
Terminale

Définition de l'intégrale
L'intégrale d'une fonction continue et positive sur un intervalle a, b représente l'aire de la surface entre la courbe de la fonction, les axes verticaux x égal à a et x égal à b, et l'axe horizontal. Cette aire est mesurée en unité d'aire, qui est un petit carré de taille 1 sur 1 dans un repère orthonormé. L'intégrale est notée par un signe mystérieux, "intégrale entre a et b de f de x dx". Si la fonction est négative, on mesure tout simplement la surface correspondante et on y met un signe moins. Si la fonction a des valeurs mixtes, on différencie les parties positives et négatives en calculant leur aire respective. Il faut toujours garder en tête que l'intégrale est positive au-dessus de l'axe des X et négative en dessous de cet axe.
Maths Spé
Analyse
Terminale

Encadrement et intuition graphique
Dans cette vidéo, on apprend comment approximer l'aire sous une courbe en utilisant des formes géométriques telles que des rectangles, des triangles, etc. Cependant, pour les courbes plus complexes, on doit utiliser des méthodes d'approximation telles que les rectangles supérieurs et inférieurs, le point milieu et les trapèzes. Lorsque le nombre de rectangles augmente et leur finesse diminue, alors on atteint la vraie valeur de l'aire sous la courbe. En utilisant des graphiques pour illustrer ces méthodes, nous pouvons mieux comprendre comment est effectué le calcul d'aires et d'intégrales.
Maths Spé
Analyse
Terminale
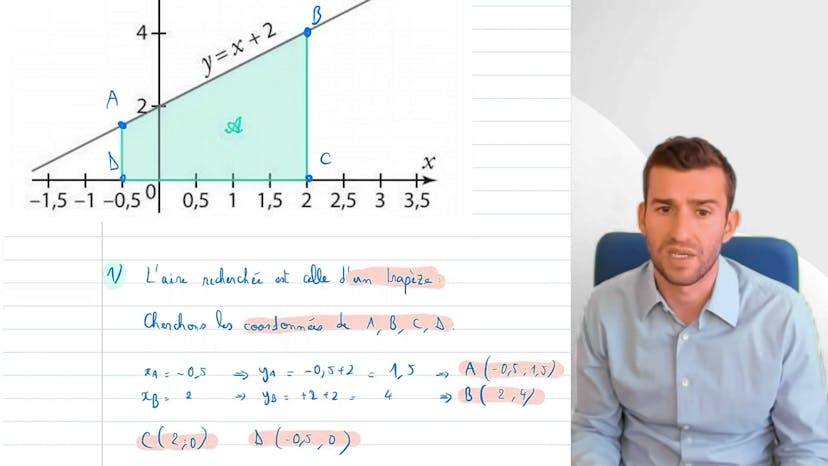
Intégrale et Aire
Ce cours explique comment calculer une intégrale géométriquement, sans utiliser la fonction. Cette méthode est valable pour des formes géométriques simples, comme un trapèze, comme dans l'exemple présenté avec une fonction affine. Pour calculer l'intégrale, il faut trouver la hauteur, la largeur et la longueur des bases du trapèze en question. On peut le faire en trouvant les coordonnées des points a, b, c et d qui le définissent. Ensuite, on calcule les longueurs de chaque côté du trapèze et on applique la formule de l'aire du trapèze: la moyenne des deux bases fois la hauteur. Dans cet exemple, l'aire du trapèze est de 6,875, ce qui correspond à la valeur de l'intégrale recherchée. C'est une méthode alternative au calcul de primitives dans certains cas.
Maths Spé
Analyse
Terminale
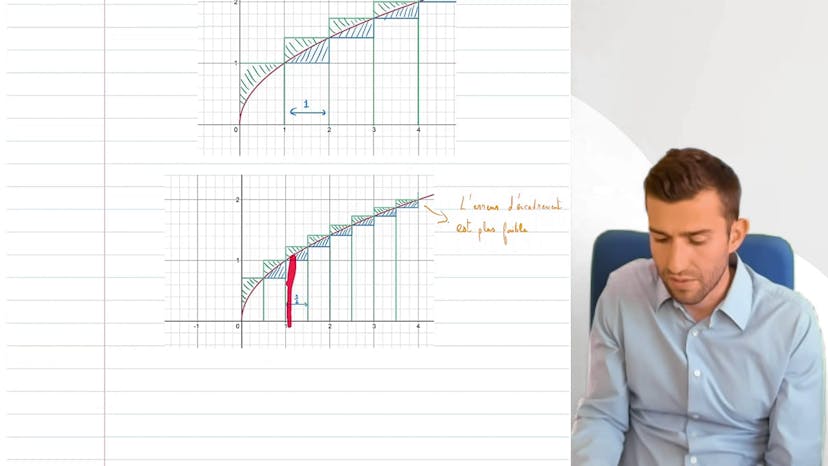
Méthode des Rectangles
Dans ce cours de mathématiques, on utilise la méthode des rectangles pour encadrer l'aire sous une courbe dont l'intégrale n'a pas une forme géométrique simple. La fonction à intégrer est croissante et on encadre son aire en utilisant les airs de petits et grands rectangles. L'encadrement obtenu ne sera pas très précis, mais en diminuant la largeur des rectangles, on peut augmenter la précision de l'encadrement. En fin de compte, on encadre l'intégrale de la fonction de 0 à 4 à l'aide de deux bornes. En résumé, la méthode d'encadrement est une méthode utile pour trouver une valeur approximative de l'intégrale d'une fonction lorsque l'on ne peut pas trouver sa primitive.
Maths Spé
Analyse
Terminale

Introduction
Dans ce sous-chapitre sur les intégrales, on va explorer le lien entre les méthodes de calcul d'R sous une courbe et les primitives. Ce lien va nous permettre de calculer les R de manière exacte, sans approximation. Ce qui va être intéressant, c'est que ça va aller dans les deux sens, on pourra calculer parfaitement les R sous une courbe en utilisant leurs primitives et on pourra également s'attaquer à des primitives qui ne sont pas calculables. On va aussi avoir quelques propriétés sur les intégrales en général, ainsi que des méthodes de calcul qui vont suivre ces points de courbe habituels. En somme, on va apprendre le théorème fondamental, qui définit l'existence d'une primitive avec une certaine formule pour la primitive, la condition suffisante d'existence d'une primitive, ainsi que des propriétés générales et des méthodes pour calculer une intégrale.
Maths Spé
Analyse
Terminale

Théorème fondamental : énoncé
Dans cette vidéo, l'auteur présente le théorème fondamental de l'analyse, qui relie la notion de primitive et l'intégrale d'air sous la courbe. Soit f une fonction continue et positive sur un intervalle a, b. La fonction F définie comme l'intégrale de f entre a et x est dérivable et sa dérivée est égale à f elle-même. Ainsi, F est une primitive de f. L'auteur illustre ce théorème en prenant l'exemple d'une fonction parabolique, calculant l'air sous la courbe et traçant des fonctions qui correspondent à l'air sous la courbe pour différentes valeurs de x. En examinant son dessin, il montre comment la fonction dérivée est liée à l'air sous la courbe. La vidéo s'achève sur une explication visuelle de l'interprétation graphique de la démonstration du théorème.
Maths Spé
Analyse
Terminale

Intégrale et Primitive : calcul
Dans cette vidéo, on présente une propriété fondamentale du chapitre de calcul intégral. Cette propriété permet de calculer une intégrale à l'aide d'une primitive, c'est-à-dire une fonction dont la dérivée est la fonction à intégrer. Cette propriété est distincte du théorème fondamental, qui garantit l'existence d'une primitive sous forme d'un calcul intégral. Pour démontrer cette propriété, on utilise le théorème fondamental et on distingue deux cas : si la primitive est celle du théorème fondamental, alors la propriété est prouvée facilement ; sinon, on utilise le fait que toutes les primitives d'une fonction sont de la forme de la primitive connue plus une constante, afin de prouver la propriété. On peut ainsi calculer l'aire sous la courbe d'une fonction continue pour n'importe quel intervalle.
Maths Spé
Analyse
Terminale

Propriétés 1 : intuitives !
Dans cette vidéo, nous abordons les propriétés de l'intégrale. La première est la linearité, qui mentionne que si vous prenez l'air sous une courbe, cela équivaut à multiplier la hauteur par un certain facteur. La deuxième propriété est la cumulativité, qui signifie que l'air sous une courbe combinée est la somme de l'air sous les courbes individuelles. La troisième propriété concerne les bornes, où l'air sous une courbe entre un point et lui-même est nul, et l'air entre deux points peut être pris avec un signe négatif si les points sont inversés. Enfin, la relation de Schall stipule que l'air total sous une courbe est la somme des airs entre les points où la courbe rencontre l'axe horizontal. Ces propriétés sont intuitives et faciles à comprendre pour les débutants en mathématiques.
Maths Spé
Analyse
Terminale
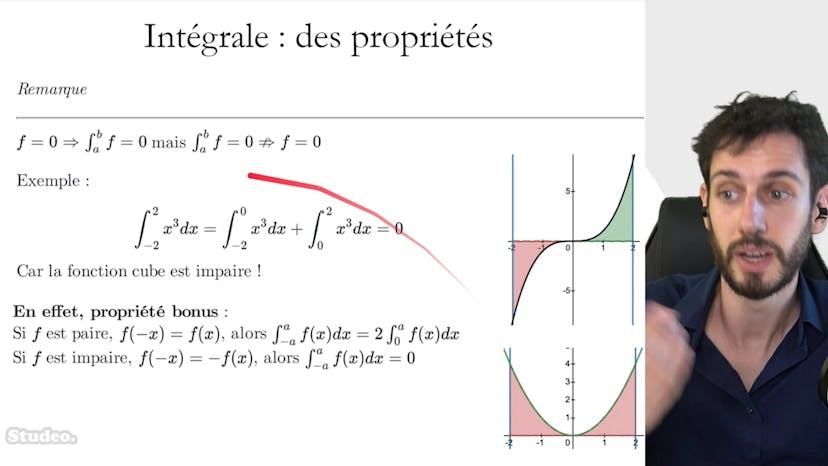
Propriétés 2 : remarques pratiques
Ce cours traite de trois propriétés importantes en mathématiques. La première propriété concerne les fonctions nulles qui ont une intégrale nulle, mais cela ne signifie pas que toutes les fonctions dont l'intégrale est nulle sont nulles aussi. La deuxième propriété traite des fonctions paires et impaires. Les fonctions paires ont une intégrale symétrique centrée sur 0, tandis que les fonctions impaires ont une intégrale nulle sur un intervalle symétrique centré sur 0. La troisième propriété concerne les fonctions périodiques, dont l'intégrale sur tout intervalle de taille t est la même. Ces propriétés sont très utiles pour résoudre des problèmes et pour gagner du temps en étudiant des fonctions.
Maths Spé
Analyse
Terminale
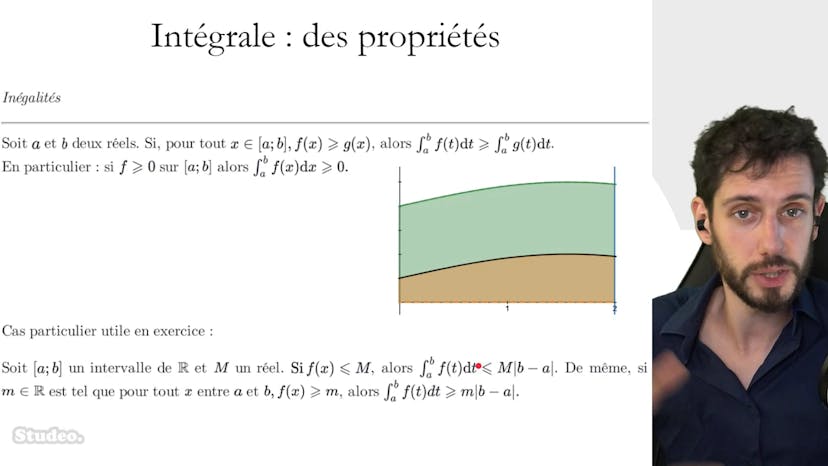
Propriétés 3 : inégalités
Dans cette vidéo, nous apprenons que les intégrales de deux fonctions f et g sont classées dans le même ordre si f est toujours plus grande que g pour toute x de a à b. Si g est la fonction nulle et que f est toujours plus grande que 0, alors l'intégrale de f est toujours positive. Si f est majorée par une fonction constante égale à M, alors l'intégrale de f est plus petite que l'intégrale de M entre a et b. Si f est minorée par une petite M, alors l'intégrale de f est plus grande que M fois b moins a en valeur absolue. Ces propriétés sont très simples, mais il est important de les connaître pour résoudre des exercices. Si vous avez des doutes, posez des questions dans la FAQ.


