 Tous les sujets
Tous les sujets Maths
Maths Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée Prépa Examens
Prépa Examens
Terminale
Première
Seconde
MPSI/PCSI
2BAC SM Maroc
 Tous les sujets
Tous les sujets Maths
Maths Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée Prépa Examens
Prépa Examens
Maths Spé
Analyse
Terminale

Calcul d'Intégrale avec Primitive
Le cours traite de la première méthode sur le calcul intégral. L'enjeu principal du chapitre est de trouver une primitive pour l'intégrale à résoudre. L'exercice présenté consiste à calculer l'intégrale de 0 à pi de x² moins cos de 2x. Pour cela, il faut trouver une primitive. La primitive de x² est x³ et celle de cos de 2x est 1/2 sin 2x. Attention aux erreurs de signes lors de l'application du théorème fondamental, mieux vaut écrire les signes avec des parenthèses avant de développer. En simplifiant les calculs, l'intégrale finale est égale à pi au cube sur 3.
Maths Spé
Analyse
Terminale
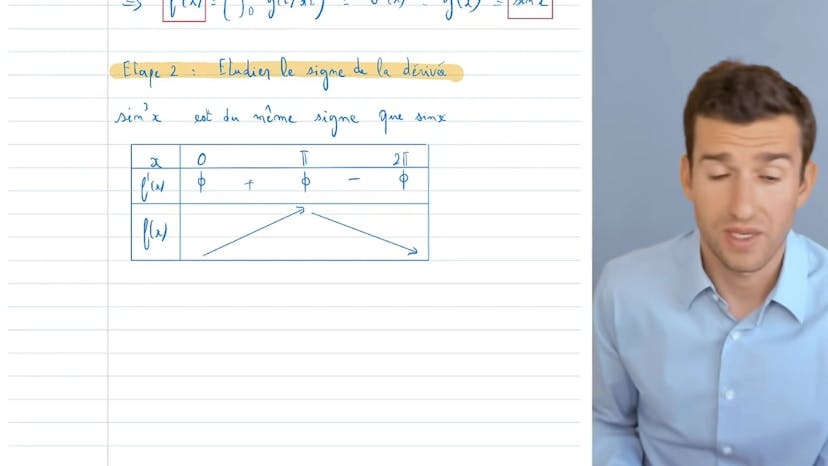
Fonction définie par une Intégrale
Étudier les variations d'une fonction peut se faire en calculant sa dérivée pour déterminer le signe, puis la monotonie. Heureusement, pour une intégrale (intégrale de a à x de u de t), sa dérivée est facile à calculer avec u. Cependant, il faut faire attention aux bornes pour que cela marche bien. Pour l'intégrale de 0 à π de sin³(t), il est donc important de faire attention au programme d'intégration pour déterminer la dérivée. Ensuite, il est facile de déduire les variations. Sin³(t) étant du même signe que sin(x), la fonction est croissante jusqu'à π/2, puis décroissante. Il est également important de faire attention aux variables si elles sont locales ou pas et de ne pas inverser les bornes.
Maths Spé
Analyse
Terminale

Linéarité d'une Intégrale
Dans ce cours de mathématiques, l'utilisation de la linéarité de l'intégrale est expliquée pour faciliter le calcul des primitifs. Le professeur nous donne un exemple, en nous faisant étudier la fonction f=x^2. Il nous demande tout d'abord de montrer que la fonction F proposée (F(x)=1/3x^3) est une primitive de f. Pour cela, il suffit de dériver F et de vérifier si la dérivée est bien égale à f. Dans la deuxième partie du cours, nous devons déterminer l'intégrale de 0 à 1 de 3x-2e^(x). Il y a une erreur d'énoncé à corriger (le t est remplacé par x). Pour trouver une primitive, le professeur rappelle la règle selon laquelle lorsque l'on a un polynôme multiplié par une exponentielle, on doit utiliser une IPP. En posant u=3x-2, et en utilisant la dérivée de u et la primitive de e^x pour v, il résout l'intégrale et trouve la primitive. Il conclut ensuite en rappelant que lorsqu'on a cette même forme de polynôme multipliée par une exponentielle, on doit toujours penser à utiliser cette méthode.
Maths Spé
Analyse
Terminale

Encadrer une Intégrale
Ce cours commence par montrer que pour tout x supérieur à 1, e de moins x carré est toujours positif. Ensuite, en utilisant les propriétés de la fonction exponentielle, on montre que cette fonction est inférieure à e de moins x. On en déduit donc un encadrement de l'intégrale de cette fonction sur l'intervalle de 1 à 2. En utilisant la propriété de monotonie de l'intégrale, on trouve finalement que cette intégrale est comprise entre 0 et e de moins 1 moins e de moins 2.
Maths Spé
Analyse
Terminale
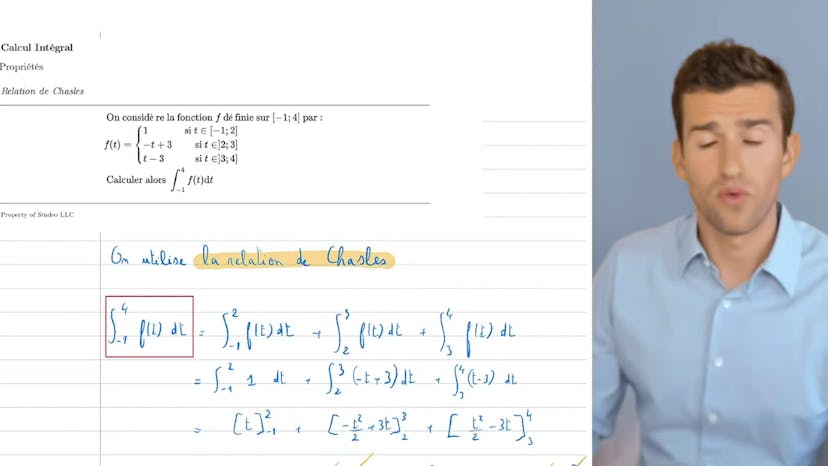
Relation de Chasles
Dans cette vidéo, l'objectif est de calculer une intégrale en utilisant les relations de Schall. On a une fonction f avec différentes expressions selon l'intervalle. Grâce à cette méthode, on peut découper l'intégrale en plusieurs morceaux et utiliser des fonctions usuelles faciles à primitiver pour les calculs. Ensuite, on vérifie que le chiffre de départ est égal à celui d'arrivée pour que ça se rejoigne bien et on peut passer par où on veut pour faire les calculs. Cette méthode est simple et facile à appliquer si on fait attention à ces détails.
Maths Spé
Analyse
Terminale

Introduction
Ce sous-chapitre sur les intégrales, les applications et calculs aborde l'utilisation de méthodes comme l'intégration par partie pour calculer des primitives plus complexes qui ne figurent pas dans les tables classiques. Il permet également de calculer des r sous les courbes (r entre des courbes) en utilisant le lien entre r et primitive établi dans le sous-chapitre précédent. Il aborde également la définition de la valeur moyenne d'une fonction, avec des méthodes associées. En résumé, ce sous-chapitre permet de calculer des r sous une courbe, entre deux courbes, de calculer la valeur moyenne d'une fonction et de faire du calcul intégral par intégration par partie, notamment à travers des exercices difficiles.
Maths Spé
Analyse
Terminale

Intégration par Parties
L'intégration par partie est une formule importante en mathématiques pour calculer des primitives ou résoudre des équations différentielles. La formule en gros dit que l'intégrale de uv' est égale à la primitive de u x v entre a et b moins l'intégrale entre a et b de u' x v. Elle est utile pour des intégrales compliquées où il n'est pas possible de trouver une primitive facilement. L'astuce consiste à interpréter les termes du produit comme u et v', puis à appliquer la formule pour simplifier l'inté
Maths Spé
Analyse
Terminale

Aire entre 2 courbes
Dans cette vidéo, on apprend comment calculer l'air entre deux courbes en utilisant le théorème suivant : Soit f et g, deux fonctions continues sur un intervalle i, tel que f2x est toujours plus petite que g2x. L'air exprimé en unité d'air du domaine, compris entre x égal a et x égal b, donc les bords de l'intervalle, et la courbe de f et la courbe de g, vaut l'intégrale entre a et b de g2x moins f2x. Pour illustrer cette propriété, l'auteur utilise deux fonctions f en rouge et g en bleu et montre que l'air entre les deux courbes est égal à l'intégrale de f moins g lorsque f est au-dessus de g et à l'intégrale de g moins f lorsque g est au-dessus de f.
Maths Spé
Analyse
Terminale
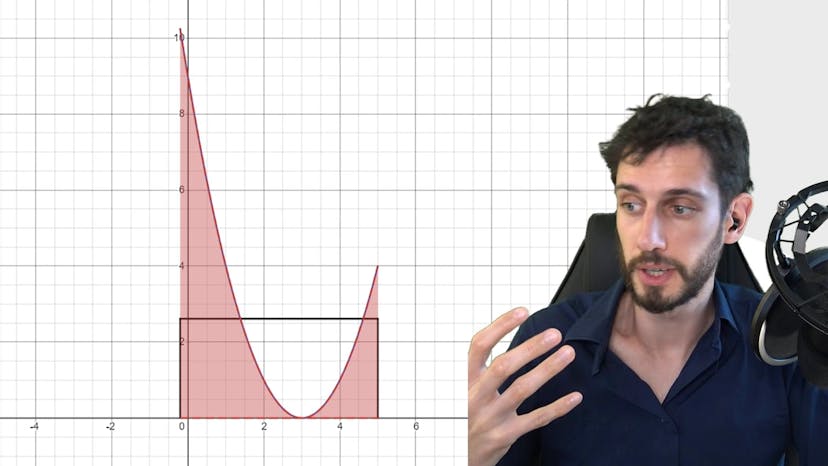
Valeur Moyenne
La valeur moyenne d'une fonction est définie comme le nombre mu égal à 1 sur b moins a fois l'intégrale entre a et b de f, où f est une fonction continue. On peut voir la valeur moyenne comme une moyenne arithmétique des rectangles infiniment fins entre a et b. Elle peut également être comprise géométriquement comme la valeur constante telle que l'air sous la courbe de la fonction constante soit égale à l'air sous la courbe de f. La valeur moyenne est la hauteur du rectangle parfait qui a la même aire que l'aire sous la courbe de f. Elle est utile pour résoudre des exercices de méthodes. Si vous avez des questions, la FAQ est ouverte.
Maths Spé
Analyse
Terminale

Intégration par Parties : Calcul
La méthode d'intégration par partie est utilisée pour calculer des intégrales en décomposant une fonction en deux parties et en utilisant les propriétés de la dérivée du produit. Voici les étapes principales pour appliquer cette méthode :
1. La formule de l'intégration par partie est donnée par l'intégrale de U'V moins l'intégrale de UV'. Cette formule est basée sur la dérivée du produit, UV' = U'V + UV.
2. Il est important de choisir judicieusement les deux parties U' et V afin d'avoir un résultat simplifié. Trois points sont à considérer :
a. Il doit y avoir un produit dans l'intégrale pour pouvoir appliquer la méthode.
b. Au moins l'une des deux fonctions doit avoir une primitive facile à calculer.
c. La dérivée de l'autre fonction doit simplifier le calcul.
3. Pour appliquer la méthode, on calcule U'V et UV' en utilisant les choix de U' et V. On intègre U'V et on trouve la primitive de UV'.
4. On simplifie l'expression obtenue en remplaçant les termes entre crochets par leur valeur. On continue ensuite avec le calcul et on obtient le résultat final.
Dans cet exemple spécifique, l'intégrale à calculer est l'intégrale de X ln(X) entre 1 et E. On choisit U' = X et V = ln(X) et on calcule U'V et UV'.
En utilisant la formule de l'intégration par partie, on obtient une expression simplifiée : X²/2-ln(X)/2.
En évaluant cette expression entre 1 et E, on obtient le résultat final : E²/2-1/4.
Il est important de noter que l'ordre de dérivation et d'intégration peut être inversé dans certains cas, mais il est préférable de choisir la méthode qui facilite le calcul. Pour éviter les erreurs, il est recommandé d'écrire U', U, V et V' clairement afin de suivre les étapes plus facilement.
Maths Spé
Analyse
Terminale

Aire sous une Courbe : Calcul
Dans ce cours, nous abordons le calcul d'erreurs sous une courbe à l'aide d'intégrales. Deux exemples sont présentés pour illustrer cette méthode.
Le premier exemple concerne l'erreur entre la courbe CF, définie par l'équation f2x=x²-4, et l'axe d'étape 6, entre les valeurs x=-2 et x=2. Pour calculer cette erreur, nous devons trouver la primitive de la fonction x²-4 à l'intérieur de l'intégrale. En trouvant la primitive, qui est un tiers de x au cube moins 4x, nous appliquons le théorème fondamental pour obtenir l'erreur. Nous effectuons les calculs en faisant attention aux signes négatifs. Dans ce cas, l'erreur est égale à -32/3.
Le deuxième exemple concerne l'erreur entre la courbe et l'axe des abscisses entre les valeurs x=-5 et x=1. Encore une fois, nous devons trouver la primitive de la fonction x²-4 et calculer l'intégrale entre les bornes. En simplifiant les calculs, nous trouvons une erreur de 18. Visuellement, la courbe présente une partie positive et une partie négative, mais la somme des deux nous donne une erreur positive.
Il est important de noter que la variable d'intégration est spécifiée dans l'équation et ne peut pas être modifiée. Dans le premier exemple, la variable est x, tandis que dans le deuxième exemple, elle est t.
En résumé, ce cours explique comment calculer les erreurs sous une courbe à l'aide d'intégrales. Deux exemples sont présentés, montrant les calculs et les erreurs obtenues.
Maths Spé
Analyse
Terminale
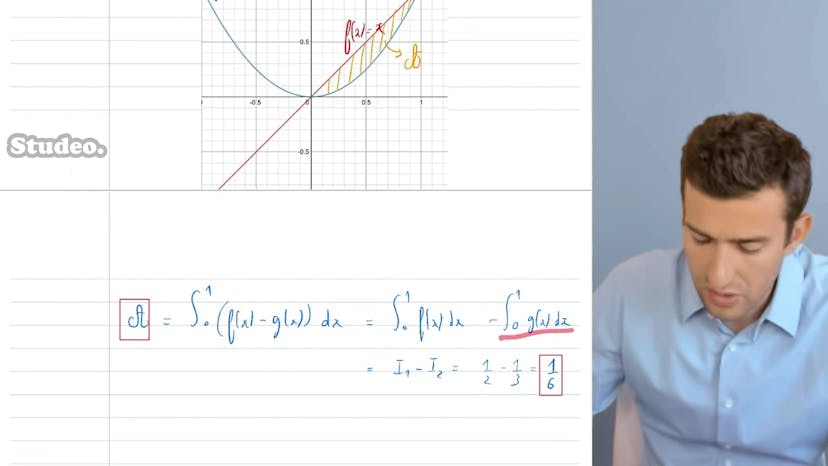
Aire entre 2 Courbes
Dans cette vidéo, nous apprenons comment calculer l'R entre deux courbes, à savoir les fonctions f2x = x et g2x = x², sur l'intervalle [0, 1]. Pour cela, il est nécessaire de trouver les primitives des deux fonctions. Pour f2x, la primitive est f2x = x²/2, tandis que pour g2x = x², la primitive est g2x = x³/3.
En utilisant le théorème fondamental, nous pouvons représenter visuellement les deux fonctions f et g. L'R sous la courbe est la zone qui est encadrée et qui sera appelée "1". Pour faciliter le calcul, nous choisissons de prendre l'R plutôt positif en prenant la différence entre la fonction supérieure et la fonction inférieure sur l'intervalle. Dans ce cas précis, f est toujours supérieure à g sur l'intervalle [0, 1].
En calculant l'intégrale de f2x - g2x, nous obtiendrons la valeur de notre R entre 0 et 1. En utilisant les propriétés de l'intégrale, nous pouvons écrire cette différence comme l'intégrale de f moins l'intégrale de g sur l'intervalle [0, 1].
Après avoir effectué les calculs nécessaires, nous trouvons que l'intégrale de f2x de 0 à 1 est égale à 1/2 et l'intégrale de g2x de 0 à 1 est égale à 1/3. Par conséquent, la différence entre ces deux valeurs est de 1/6. Ainsi, l'R entre les deux courbes sur l'intervalle [0, 1] est de 1/6. C'est ainsi que l'on calcule l'R entre deux courbes.


