Cours d'apprentissage en ligne

Dépôt d’argent

Dans cette vidéo, l'auteur explique le processus d'un dépôt d'argent sur une statuette métallique à l'aide d'un électrolyseur. Les réactions se produisant à chaque électrode sont les suivantes: - À l'électrode en argent: Ag+ + e- -> Ag (oxydation de l'ion argent en argent solide) - À l'électrode en graphique: 2H2O -> O2 + 4H+ + 4e- (oxydation de l'eau en dioxygène) L'équation de la réaction d'électrolyse est obtenue en combinant linéairement les demi-équations. Dans ce cas, elle est donnée par: 4Ag+ + 2H2O -> 4Ag + O2 + 4H+ Ensuite, l'auteur aborde la quantité d'électricité Q qui a traversé l'électrolyseur pendant une durée de 15 minutes, avec une intensité du courant constante à 80 mA. Il explique qu'il y a deux façons d'exprimer la charge débitée par une pile: la vision chimique, où la charge est égale au nombre de molles d'électrons échangés multiplié par le faraday (F), et la vision électrique, où la charge est égale à l'intensité du courant multipliée par la durée d'électrolyse. Dans ce cas, la charge est de 72 coulombs. Ensuite, l'auteur répond à la question sur la quantité de matière d'argent déposée sur la statuette. Il explique qu'il faut relier le nombre de molles d'électrons échangés au nombre de molles d'argent. Il utilise la relation Q = nE * F, où nE est le nombre de molles d'électrons échangés, E est la charge d'une molle d'électrons et F est le nombre d'Avogadro. Il conclut que le nombre de molles d'argent déposé est de 7,5 x 10^-4 molles, ce qui correspond à une masse de 80 mg en multipliant par la masse molaire. Enfin, l'auteur aborde la question du volume de gaz formé, en particulier le dioxygène. Il explique que le nombre de molles d'électrons échangés peut être lié au nombre de molles de dioxygène formé. Il utilise la relation nO2 = nE / 4, où nO2 est le nombre de molles de dioxygène formé. En considérant le dioxygène comme un gaz parfait, il peut relier le nombre de molles d'O2 au volume du gaz en utilisant la relation V = nO2 * R * T / P, où V est le volume, R est la constante des gaz parfaits, T est la température et P est la pression. Il conclut que le volume de dioxygène formé est de 4,6 mL pour une pression de 1 bar et une température de 298 K. En résumé, cette vidéo explique le processus d'un dépôt d'argent sur une statuette métallique à travers l'utilisation d'un électrolyseur. Elle aborde les réactions électrochimiques qui se produisent à chaque électrode, la quantité d'électricité traversant l'électrolyseur, la quantité de matière d'argent déposée et le volume de gaz formé.

Physique-Chimie

Chimie

Eau de Javel

Dans cette vidéo, on aborde la fabrication de l'eau de Javel, en particulier la production de l'ion hypochlorite Cl-. Cette fabrication se fait par électrolyse d'une solution aqueuse de chlorure de sodium Na+ Cl-. Les électrodes utilisées sont en graphite inerte. Sur l'anode, du dichlore gazeux (Cl2) se forme, tandis que sur la cathode, de l'eau (H2O) réagit pour produire du dihydrogène (H2). Pour la première question, on doit écrire la demi-équation de la réaction sur l'anode et en déduire l'équation de la réaction d'électrolyse. La demi-équation sur l'anode est : 2Cl- = Cl2 + 2e-. En sommant cette équation avec celle sur la cathode, qui est donnée, on obtient l'équation d'électrolyse : 2H2O + 2Cl- = Cl2 + H2 + 2OH-. Pour la deuxième question, il faut faire un schéma du montage en précisant le sens de circulation des porteurs de charge. L'anode est à droite et la cathode est à gauche. À l'anode, l'oxydation se produit, avec la libération de Cl2 gazeux. À la cathode, la réduction se produit, avec la formation de H2 gazeux. Les électrons sont libérés à l'anode et consommés à la cathode. Ainsi, le sens de déplacement des électrons est de la droite vers la gauche, et le sens de déplacement du courant est inversé, de la gauche vers la droite. Enfin, pour la troisième question, on nous demande d'écrire l'équation d'oxydoréduction correspondant à la réaction du dichlore avec lui-même. On équilibre les demi-équations des deux couples redox (Cl2/Cl- et Cl-/Cl2) et on les combine. On obtient donc l'équation bilan : 2Cl2 + 2H2O = 2Cl- + 2Cl- + 4H+. Cette réaction montre comment le dichlore agit à la fois comme oxydant et comme réducteur sur lui-même. En résumé, cette vidéo explique le processus de fabrication de l'eau de Javel par électrolyse d'une solution de chlorure de sodium. Les différentes réactions, les équations et le schéma du montage sont détaillés.

Des inégalités classiques

Dans cet exercice, on étudie différentes inégalités en utilisant les concepts de convexité et de concavité. La première inégalité à démontrer est que pour tout réel X, l'exponentiel de X est supérieur à 1+X, même si X est non nul. On commence par chercher un lien entre l'exponentiel de X et 1+X. On remarque que 1+X peut s'écrire comme l'exponentiel de 0 fois X moins 0 plus l'exponentiel de 0. On reconnaît ainsi l'équation de la tangente à la courbe de l'exponentiel de X au point d'abscisse X=0 et d'ordonnée 1. En étudiant la convexité de la fonction exponentielle, on montre que la courbe de cette fonction est strictement au-dessus de cette tangente, en dehors du point de contact. On en déduit que pour tout X réel, l'exponentiel de X est supérieur ou égal à 1+X, avec égalité seulement en X=0. Ensuite, on souhaite montrer que le logarithme de 1+X est inférieur ou égal à X. En étudiant la convexité de la fonction logarithme de 1+X, on montre qu'elle est strictement concave. On en déduit que la courbe de cette fonction est strictement en-dessous de sa tangente en X=0. On écrit donc l'équation de cette tangente et on l'utilise pour montrer que le logarithme de 1+X est inférieur ou égal à X, avec égalité en X=0. Finalement, on souhaite encadrer la fonction sinus de X entre pi/2 et X pour X dans l'intervalle [0, pi/2]. On étudie la convexité de la fonction sinus et montrons qu'elle est concave sur cet intervalle. On utilise ensuite une tangente en X=0 pour montrer que la fonction sinus de X est inférieure ou égale à X. Enfin, on utilise une corde entre les points (0, pi/2) et (pi/2, 1) pour montrer que la fonction sinus de X est supérieure ou égale à pi/2. On conclut donc que la fonction sinus de X est bien encadrée entre pi/2 et X pour X dans l'intervalle [0, pi/2].

Le vin et ses composants (1)

Dans cette vidéo, on s'intéresse à la case blanche d'un vin, qui est un précipité blanc dû à une trop grande concentration des ions fer. Pour mesurer cette concentration, on réalise un titrage spectrophotométrique en plusieurs étapes. Tout d'abord, on oxyde les ions fer 2 en fer 3, puis on fait réagir ces derniers avec des ions thiocyanate pour former un composé coloré. On réalise ensuite des solutions étalons avec différentes concentrations de ce composé, et à partir de la couleur de la solution de vin, on peut déterminer sa concentration en fer. Les ions thiocyanate sont ajoutés en excès pour que tous les ions fer réagissent. On prépare également une solution de vin en mélangeant du vin blanc, de l'acide chlorhydrique, une solution de thiocyanate et de l'eau oxygénée. On mesure l'absorbance de plusieurs solutions, ce qui permet de tracer une courbe d'étalonnage. En utilisant la loi de Beer-Lambert, on peut établir une relation entre l'absorbance et la concentration massique en fer. On obtient une absorbance de 0,16 pour le vin étudié, ce qui correspond à une concentration de 1,7 mg/L de fer. Comme cette concentration est inférieure à 10 mg/L, il n'y a aucun risque de formation de case blanche dans ce vin.

Le vin et ses composants (2)

Dans cette vidéo, Théobald de Cidéo explique un exercice de chimie sur l'estérification dans le vin. Il s'intéresse à la durée de ce processus et à sa relation avec les conditions expérimentales. Le protocole consiste à mélanger de l'acide éthanoïque pur avec de l'éthanol pur dans un bain au glace. Ensuite, on prépare plusieurs tubes contenant du mélange réactionnel et une solution d'hydroxyde de sodium. On plonge les tubes dans un bain marie à différentes températures, puis on les met dans un bain au glace pour arrêter la réaction. Ensuite, on réalise un titrage de l'acide éthanoïque restant dans chaque tube. La première question concerne le placement du mélange réactionnel dans un bain au glace avant l'instant T0 et avant le titrage. La réponse est que la température est un facteur cinétique et en le plaçant dans un bain au glace, on bloque la réaction avant le titrage. La deuxième question consiste à montrer que le mélange réactionnel est équimolaire. En calculant la quantité de matière en acide éthanoïque et en éthanol à partir de leur masse volumique et de leur volume, on trouve que les deux quantités sont équivalentes. La question suivante demande de vérifier que la quantité d'acide contenue dans chaque tube à la date T0 est de 17,3 millimoles. En utilisant les données fournies dans l'énoncé, on calcule cette quantité et on trouve le résultat demandé. Ensuite, on explique le rôle du bleu de thymol, qui est un indicateur coloré utilisé lors du titrage pour repérer l'équivalence. On définit aussi l'équivalence comme le moment du titrage où les réactifs ont été apportés en proportion stoichiométrique. On montre ensuite que la quantité d'acide restant à la date Ti dans un tube est donnée par CbxVbi, où C est la concentration de la solution d'hydroxyde de sodium et Vbi est le volume à l'équivalence pour le tube i. Enfin, on détermine la quantité d'éthanoate d'éthyle produite dans chaque tube à partir de la relation Ni = N0 - CbVbi. On utilise un tableau d'avancement pour établir les quantités initiales et finales des réactifs. On applique cette formule pour chaque tube afin de remplir un tableau de résultats expérimentaux. Il reste à trouver la valeur de la quantité de matière N2 manquante dans le tableau en utilisant la formule N2 = N0 - CbVb2. On effectue le calcul et on obtient la valeur de N2. Dans la prochaine vidéo, Théobald continuera cet exercice.

Le vin et ses composants (3)

Dans cette vidéo, Théobald de Cidéo conclut l'exercice sur le processus d'estérification du vin. Il se concentre sur la vitesse d'apparition des estères. Pour cela, il utilise un graphe qui montre la quantité de matière d'estère formée au fil du temps. Théobald explique que la vitesse volumique d'apparition d'un estère est le quotient de 1 sur le volume de la solution, multiplié par la dérivée du nombre de molles d'estères par rapport au temps. En examinant les tangentes de la courbe, il observe que le coefficient directeur diminue au fil du temps, ce qui signifie que la vitesse volumique d'apparition diminue également. Il est ensuite demandé de déterminer la valeur de la vitesse volumique d'apparition de l'ester à 20 minutes. Théobald utilise la tangente à ce point pour trouver le coefficient directeur, qui est égal à la dérivée du nombre de molles par rapport au temps à 20 minutes. Après quelques calculs, il obtient une vitesse volumique d'apparition de 6,0 x 10^-2 molles par litre par minute. Ensuite, il est demandé de déterminer le temps de demi-réaction, qui est le temps auquel la moitié de l'ester est apparue. Théobald utilise la courbe et trouve que le temps de demi-réaction est de 6,5 minutes. Il compare ensuite ce temps à la durée mentionnée en introduction de la vidéo, selon laquelle le processus d'esterification peut prendre plusieurs jours voire des mois. Théobald explique que l'écart entre le temps de demi-réaction trouvé et le temps réel peut s'expliquer par le fait que les réactifs utilisés dans l'exercice étaient purs et non dilués, ce qui a augmenté la concentration et donc la vitesse de la réaction. Finalement, il conclut que pour obtenir une réaction rapide, il est nécessaire d'utiliser des réactifs purs et concentrés.

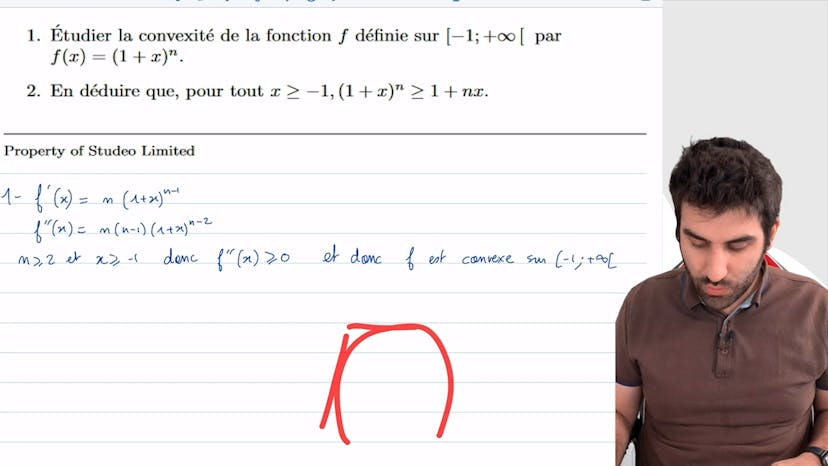
Inégalité de Bernoulli

Dans cet exercice, nous montrons l'inégalité de Bernoulli en utilisant la convexité de la fonction 1+x^n. Habituellement, cette inégalité est démontrée en utilisant le raisonnement par récurrence, mais ici nous utilisons la convexité. Pour étudier la convexité de la fonction sur l'intervalle (-1, +∞), nous dérivons deux fois la fonction et étudions le signe de la dérivée. La dérivée première est n(1+x^(n-1)) et la dérivée seconde est n(n-1)(1+x^(n-2)). Comme n>2 et x>-1, les dérivées sont positives. Ainsi, f' est positive et donc f est convexe sur (-1, +∞). Nous en déduisons alors que pour x>-1, 1+x^n > 1+nx, ce qui est l'inégalité de Bernoulli. Une propriété importante à retenir est qu'une fonction convexe est toujours au-dessus de ses tangentes. Donc, pour obtenir une inégalité avec une fonction affine, il suffit de considérer la fonction affine comme une tangente de la fonction convexe. En utilisant cette propriété, nous considérons la fonction 1+x^n comme une tangente de f au point d'abscisse 0. En vérifiant que 1+nx est bien l'équation de cette tangente, nous concluons que f(x) est plus grand que 1+nx. Ainsi, 1+x^n > 1+nx sur l'intervalle (-1, +∞).

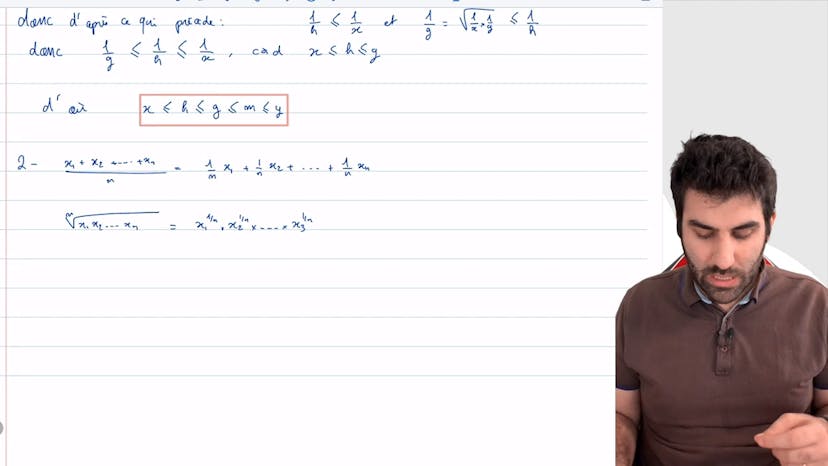
Moyennes arithmétique et géométrique

Dans cet exercice, on nous donne les définitions des moyennes arithmétique, géométrique et harmonique. Nous devons montrer que la moyenne géométrique est plus petite que la moyenne arithmétique, et que cette dernière est plus petite que la moyenne harmonique. Pour prouver cela, nous commençons par montrer que la moyenne arithmétique est plus petite que le plus grand des deux nombres. Ensuite, nous démontrons que la moyenne géométrique est plus petite que la moyenne arithmétique. Enfin, nous montrons que la moyenne harmonique est plus grande que le plus petit des deux nombres. Ensuite, nous démontrons que la moyenne géométrique est plus grande que le plus petit des deux nombres. En utilisant les inverses des nombres, nous montrons également que la moyenne harmonique est plus grande que la moyenne géométrique. Nous utilisons ensuite ces résultats pour montrer que la moyenne harmonique est entre le plus petit et le plus grand des deux nombres. Finalement, nous démontrons le cas général pour une moyenne géométrique et une moyenne arithmétique avec plus de deux nombres. Nous utilisons la convexité de la fonction logarithme pour montrer que la moyenne géométrique est plus petite que la moyenne arithmétique. En résumé, nous avons démontré que la moyenne géométrique est plus petite que la moyenne arithmétique, elle-même plus petite que la moyenne harmonique. Cette démonstration s'appuie sur les relations entre les différentes moyennes et utilise la convexité de la fonction logarithme.

Points d’inflexion

Dans cet exercice, nous allons étudier une fonction pour déterminer ses points d'inflexion. Une fonction admet un point d'inflexion en x0 si et seulement si la dérivée seconde f'' change de signe en x0. Nous allons donc calculer la dérivée seconde de la fonction. On obtient ainsi : f'' = -cos(3x) * cos(x) - cos(2x). Pour étudier le signe de cette expression, il est préférable de factoriser. En utilisant une formule trigonométrique (cos(a) + cos(b) = 2cos((a+b)/2)*cos((a-b)/2)), on peut factoriser f'' en -cos(2x) * (2cos(2x) + 1). Maintenant que f'' est factorisée, on peut étudier le signe de chaque facteur. Pour que -cos(2x) soit positif, cos(2x) doit être négatif, c'est-à-dire quand x est entre pi/4 et 3pi/4. Pour que 2cos(2x) + 1 soit positif, cos(2x) doit être supérieur ou égal à -1/2, c'est-à-dire quand x est entre 0 et 2pi/3 ou entre 7pi/3 et 2pi. En résumé, les points d'inflexion de la fonction sont de la forme pi/4 + kpi/2 en abscisse et f(pi/4 + kpi/2) en ordonnée, avec k appartenant à Z, ainsi que 2pi/3 + 2kpi et -2pi/3 + 2kpi en abscisse et f(2pi/3 + 2kpi) et f(-2pi/3 + 2kpi) en ordonnée, avec k appartenant à Z.

Majoration de f ’ grâce à f ”

Dans cet exercice, nous devons majorer une fonction de classe C2 par une autre fonction dépendant de M, le sup de la dérivée seconde sur AB. Pour justifier l'existence de M, nous utilisons l'hypothèse que F est de classe C2, ce qui signifie que la dérivée seconde est continue sur AB. Étant donné que la fonction est continue sur un segment, elle est bornée et atteint ses bornes. Par conséquent, le sup existe. On nous présente ensuite les fonctions G et H et on nous demande de montrer que G est convexe et H est concave. Pour cela, nous calculons les dérivées secondes de G et H et en étudions le signe. En utilisant la convexité de G et la concavité de H, nous déduisons une inégalité impliquant la valeur absolue de la dérivée de F. Enfin, nous regroupons les éléments pour obtenir l'inégalité finale de la valeur absolue de F.

Formule 1 et freinage

Dans cet exercice, on étudie les pilotes de Formule 1 et leur décélération avant les virages. On suggère que les circuits devraient être redessinés pour éviter aux pilotes de prendre trop de risques. On analyse le mouvement de la voiture plus le pilote et l'accélération du système. En appliquant la deuxième loi de Newton, on montre que les coordonnées du vecteur d'accélération sont -f/m et 0. On justifie également que la variation de vitesse delta v peut être exprimée comme ax * delta t. En calculant la valeur de l'accélération à partir des données de vitesse et de durée, on obtient une valeur de 4,5 m/s^2, ce qui est inférieur à la limite de tolérance de 6G mentionnée. On conclut donc que le pilote ne prend pas de risque pour sa santé pendant le freinage. Dans la deuxième partie de l'exercice, on compare la prédiction du modèle avec les mesures réelles de vitesse obtenues grâce à un capteur embarqué. On exprime la vitesse en fonction du temps et on constate que la modélisation ne correspond pas exactement à la courbe expérimentale. On remet en question l'hypothèse selon laquelle la force de frottement reste constante pendant toute la durée du freinage.