Cours d'apprentissage en ligne

Accélération d’une bille

Dans ce cours, nous allons travailler sur l'accélération d'une bille soumise uniquement à la pesanteur terrestre. Le repère utilisé est OIG. La première étape consiste à déterminer le vecteur d'accélération de la bille en utilisant la deuxième loi de Newton qui stipule que la somme des forces extérieures est égale à la masse multipliée par l'accélération. Comme la bille est soumise uniquement à son poids (P = mg), on peut écrire que MA = MG, ce qui nous donne A = G. Ensuite, on nous demande les coordonnées de l'accélération dans le repère cartésien OIG. Pour cela, nous devons décomposer le vecteur G sur la base OIG. On peut observer que G est selon moins G, donc les coordonnées de l'accélération sont -G fois G. En termes de vecteurs, la première ligne représente toujours le premier vecteur de la base (I) et la deuxième ligne représente toujours le deuxième vecteur (G). N'hésitez pas à poser vos questions si nécessaire.

Mouvement plan

Dans ce cours, Leïla explique comment déterminer le vecteur vitesse à partir d'un vecteur d'accélération. Elle rappelle la formule d'accélération comme la dérivée de la vitesse par rapport au temps et explique qu'il faut intégrer les coordonnées une par une en prenant en compte les constantes d'intégration. En intégrant les coordonnées selon X, Y et Z, Leïla obtient une vitesse constante selon Z et une vitesse qui varie avec le temps selon Y. Elle utilise ensuite les conditions initiales pour déterminer les constantes d'intégration. Elle utilise les expressions données pour obtenir les coordonnées du vecteur vitesse, notées VX, VY et VZ. Ensuite, elle analyse si le mouvement est plan en vérifiant s'il se déplace uniquement dans deux dimensions. Dans cet exemple, Leïla constate que la vitesse est nulle selon X, ce qui signifie que le mouvement ne progresse pas dans cette direction. Par conséquent, le mouvement se fait uniquement selon Y et Z, ce qui prouve qu'il est plan. Plus précisément, il est dans le plan OYZ. N'hésitez pas à poser vos questions ou à faire part de vos remarques.

Masse à l’équilibre

Aujourd'hui, nous allons étudier une masse suspendue à un fil et soumise à la tension du fil ainsi qu'à son poids. L'objectif est de montrer pourquoi cette masse ne peut pas être en équilibre. Si nous examinons rapidement le problème, il semble évident qu'il s'agit d'un pendule simple. Si je déplace le pendule d'un certain angle, il reviendra à sa position initiale, il ne restera pas là tout seul. Pour expliquer cela à l'aide des lois que vous avez étudiées dans le chapitre, nous pouvons utiliser la loi de Newton, qui stipule que la somme des forces exercées doit être nulle pour être en équilibre. Dans ce cas, la somme des forces est T (la tension du fil) plus P (le poids), et cette somme n'est pas nulle, ce qui signifie que le système n'est pas en équilibre. Pour illustrer cela, nous pouvons utiliser la relation de Charles pour faire la somme des forces vectorielles. Si je déplace le poids et le place à côté de la flèche représentant la tension, la somme des forces vectorielles est représentée par le vecteur vert. Comme ce vecteur n'est pas nul, cela signifie que la masse n'est pas en équilibre. En ce qui concerne l'équilibre, si la masse passe par l'axe vertical, le poids est dirigé vers le bas et la tension vers le haut, ce qui permet d'atteindre l'équilibre. C'est pourquoi si l'on prend un pendule et qu'on le déplace, avec le temps, il reviendra à une position verticale, car c'est là qu'il atteint l'équilibre avec une somme des forces nulle. N'hésitez pas à poser vos questions en commentaire.

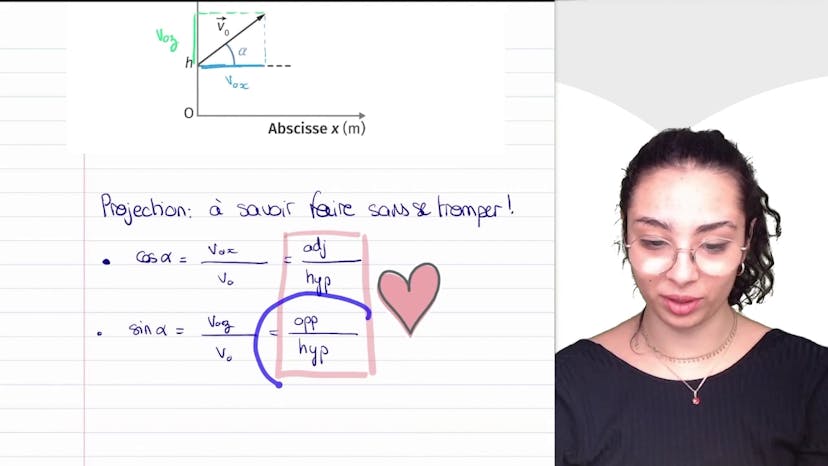
Projections

Aujourd'hui, nous allons travailler sur des projections, ce qui est important dans tous les exercices où des vecteurs sont donnés. Lorsque vous résolvez ces exercices, il est essentiel de déterminer ce qui se passe en fonction des angles. Au début, cela peut être un peu difficile car vous ne voyez pas bien où se trouvent les angles, etc. Mais nous allons le faire ensemble et vous devez garder cette technique à l'esprit. Ici, nous avons un vecteur V0 qui se décompose en composantes selon Z et X. Le but est donc de déterminer précisément les composantes selon X et Z. C'est quelque chose que vous allez trouver fréquemment dans les problèmes de mécanique. Que devons-nous faire ? Tout d'abord, nous devons regarder l'angle entre les deux. Ici, nous avons un angle avec l'horizontale appelé alpha. Dans les projections, il y a toujours des cosinus et des sinus. Avec de la pratique, vous pourrez directement identifier s'il s'agit d'un cosinus ou d'un sinus. Au début, si vous n'êtes pas sûr, je vous conseille de revenir aux formules de base. Ainsi, le cosinus d'un angle est le côté adjacent sur l'hypoténuse, tandis que le sinus d'un angle est le côté opposé sur l'hypoténuse. Il n'y a pas de tangente dans les formules de projection, car c'est toujours l'hypoténuse qui est en jeu. Je commence donc par écrire les valeurs de cos alpha et sin alpha, puis j'établis le lien avec V0x et V0y. Cos alpha est le côté adjacent sur l'hypoténuse, tandis que sin alpha est le côté opposé sur l'hypoténuse. Il ne faut pas se tromper : le côté adjacent est celui qui mène à l'angle droit, tandis que le côté opposé est de l'autre côté de l'angle droit par rapport à l'angle alpha. Une fois cela établi, j'ai une relation avec V0x, V0z, V0, cosinus et sinus. Cela me donne V0x = V0 cos alpha et V0z = V0 sin alpha. Je peux alors décomposer ces valeurs selon les vecteurs EX et EY. C'est ce qu'on appelle la projection, qui permet de déterminer les composantes selon X et Y. J'espère que cela vous a été utile, n'hésitez pas à poser vos questions.

Fondamentaux

Dans cette vidéo, Baptiste de Studio aborde le chapitre du mouvement dans un champ de gravitation. Il commence par présenter la mission Proxima de Thomas Pesquet, qui s'est rendu à bord de l'ISS à une altitude H de 400 km. L'objectif est de schématiser la trajectoire de l'ISS autour de la Terre en indiquant le rayon terrestre et l'altitude H. Baptiste souligne l'importance des schémas pour condenser les informations et faciliter la compréhension du sujet. Dans la deuxième partie de la vidéo, Baptiste demande de représenter la force FT exercée par la Terre sur l'ISS et d'en donner l'expression littérale avec les unités de chaque grandeur. Il explique que cette force est la force d'interaction gravitationnelle, qui est attractive et dépend de la masse des astres. Il rappelle qu'il est important d'adapter les notations des formules en fonction des grandeurs introduites dans l'exercice. Il donne l'expression littérale de la force d'attraction gravitationnelle en fonction de la constante de gravitation G, de la masse de l'ISS et de la Terre, et de la distance entre le centre de gravité des deux astres. Il souligne également l'importance de l'analyse dimensionnelle des unités pour arriver à la bonne unité de mesure. En conclusion, Baptiste rappelle l'importance de connaître les équations classiques et de les adapter avec les notations utilisées dans le cours. Il encourage également à ne pas négliger la réalisation de schémas, même s'ils ne sont pas parfaits, car ils peuvent aider à mieux comprendre et réussir les exercices.

1ère Loi de Kepler

Dans cette vidéo, Mathis de Studio met en pratique la première loi de Kepler en se concentrant sur la planète naine Cérès. Cérès se trouve dans la ceinture principale d'astéroïdes et a été classée comme une planète naine depuis 2008. Selon la première loi de Kepler, les planètes suivent des orbites en forme d'ellipse autour du Soleil, avec le Soleil occupant l'un des foyers de l'ellipse. Mathis explique ensuite comment représenter cette orbite en forme d'ellipse avec le Soleil et Cérès se déplaçant le long de cette trajectoire. Il souligne également que la plupart des planètes n'ont pas des orbites circulaires mais elliptiques.

Mouvement circulaire uniforme

Dans cette vidéo, nous analysons les caractéristiques du mouvement circulaire uniforme. Ce mouvement est étudié en classe de terminale et il est important de les connaître parfaitement. Pour mieux comprendre, il est conseillé de faire un schéma représentant un corps en orbite circulaire autour d'un astre dans le repère de Fresnet. De plus, il est recommandé de choisir un système d'axes approprié à l'étude de ce chapitre. Les caractéristiques du mouvement circulaire uniforme sont les suivantes : - Le rayon est constant, ce qui signifie que le mouvement est circulaire. - La norme de la vitesse est constante, même si le vecteur vitesse lui-même bouge car il tourne constamment en raison du mouvement circulaire. - L'accélération est centripète, c'est-à-dire qu'elle pointe toujours vers le centre du cercle dans lequel le mouvement s'inscrit. Ensuite, il est demandé d'exprimer la vitesse orbitale d'un satellite en fonction du rayon de son orbite et de sa période de révolution. Pour cela, il est conseillé d'exprimer la vitesse de manière littérale. En utilisant la formule classique de la vitesse (distance divisée par le temps), on peut dire que la distance parcourue par le satellite est le périmètre du cercle (2πR) et le temps mis pour parcourir cette distance est la période de révolution. En combinant ces deux informations, on obtient une expression de la vitesse orbitale en fonction du rayon et de la période. Enfin, on nous demande de déduire l'évolution de la vitesse si le rayon est divisé par 4. Pour répondre à cette question, il est important de comprendre que la vitesse n'est pas directement proportionnelle au rayon, car la période de révolution dépend également du rayon. On peut utiliser la troisième loi de Kepler, qui relie la période de révolution et le rayon, pour obtenir une expression de la vitesse en fonction du rayon. En remplaçant le rayon divisé par 4 dans cette expression, on constate que la vitesse est multipliée par 2. En conclusion, il est essentiel de comprendre les caractéristiques du mouvement circulaire uniforme et de savoir exprimer la vitesse en fonction du rayon et de la période de révolution. Il faut également être attentif aux relations entre les différentes variables afin de bien comprendre l'évolution de la vitesse en fonction de la variation du rayon. N'hésitez pas à revoir ces notions fondamentales du mouvement circulaire uniforme. Merci d'avoir suivi cette vidéo et à bientôt !

Mars et Phobos

Le cours traite du mouvement de Phobos autour de la planète Mars. On commence par déterminer les coordonnées du vecteur accélération du centre de masse de Phobos dans le repère de Fresnel lié au référentiel marso-centrique. Ensuite, on montre que le mouvement de P est uniforme, ce qui signifie que la norme du vecteur vitesse est constante. On applique le principe fondamental de la dynamique pour déterminer les forces qui s'appliquent à Phobos, en particulier la force gravitationnelle. On utilise ensuite le théorème fondamental de la dynamique pour relier l'accélération à la force gravitationnelle. En projetant cette relation sur les vecteurs tangentiels et normaux, on montre que le mouvement est uniforme. Il est important de retenir le cadre du repère de Frenet et d'utiliser les repères associés de manière efficace dans les problèmes de mouvement en champ de gravitation.

Hubble

Dans cette vidéo, nous étudions le télescope spatial Hubble, un outil important en astrophysique. Le télescope est placé en orbite autour de la Terre à une altitude de 600 km. En utilisant la deuxième loi de Newton, nous déterminons les coordonnées du vecteur accélération du centre de masse du télescope dans le repère de Frenet lié à la Terre. Nous décomposons la force gravitationnelle appliquée au télescope et établissons les composantes de l'accélération dans les directions tangentielle et normale. Ensuite, nous calculons les coordonnées du vecteur vitesse du télescope, qui est seulement dans la direction tangentielle. En utilisant une relation précédemment établie, nous trouvons la norme de la vitesse et ses composantes dans le repère de Frenet. Enfin, nous calculons la valeur de la vitesse du télescope dans le référentiel géocentrique, qui est de 7,56 km/s.

Dysnomia et Eris

Le cours parle du mouvement de Dysnomia, une lune d'Eris, une planète naine. Eris orbite autour du Soleil et a un satellite naturel appelé Dysnomia. Le mouvement de Dysnomia est supposé circulaire et uniforme. Le référentiel utilisé pour étudier ce mouvement est considéré comme galiléen. Les caractéristiques du vecteur accélération du centre de masse de Dysnomia sont que son mouvement est circulaire avec une acceleration centripète dirigée vers le centre d'Eris et de norme constante. La période de révolution de Dysnomia, TD, est donnée par l'équation TD = 2pi racine carrée RD au cube divisé par GME. Cette équation est déduite en utilisant la troisième loi de Kepler qui décrit la relation entre la période de révolution, le rayon de l'orbite et la masse de l'astre autour duquel on tourne. En isolant la masse de Eris, Me, dans cette expression, on peut la calculer en utilisant les valeurs numériques de G, RD et TD. La masse de Eris est ainsi évaluée à 1,64 x 10^22 kg, ce qui en fait une planète naine assez massive.

Balance cosmique

Dans cette vidéo, on explique pourquoi la troisième loi de Kepler est une "balance cosmique". On commence par présenter un tableau avec la période de révolution et le rayon orbital de différentes planètes du système solaire. Ensuite, on établit l'expression de la vitesse du centre de masse d'une planète dans le référentiel héliocentrique en utilisant le PFD et en considérant la force gravitationnelle comme seule force agissant sur la planète. On utilise ensuite le théorème fondamental de la dynamique pour obtenir une expression de la norme de la vitesse de la planète. Ensuite, on déduit l'expression de la période de révolution de la planète en fonction du rayon orbital, de la constante gravitationnelle et de la masse du soleil en utilisant la relation entre la vitesse et la période de révolution. On montre ensuite que le rapport entre la période de révolution et le rayon orbital au cube est égal à une constante, ce qui vérifie la troisième loi de Kepler. On explique également comment déterminer la masse du soleil à partir de la constante gravitationnelle et des valeurs de la période de révolution et du rayon orbital. Enfin, on justifie pourquoi la troisième loi de Kepler est une "balance cosmique" en montrant que la période de révolution et le rayon orbital varient de manière liée et que le rapport entre les deux doit être constant. On conclut en qualifiant la troisième loi de Kepler de "balance cosmique" car elle équilibre la période de révolution et le rayon de manière directe.