Cours d'apprentissage en ligne

Énergie échangée

Dans cette vidéo, on aborde le concept d'énergie échangée par un glaçon. Pour déterminer cette énergie et la commenter, on utilise la capacité calorifique massique de la glace (représentée par une grandeur particulière, C), qui correspond à l'énergie que peut emmagasiner le système (la glace dans ce cas). La capacité calorifique massique est représentée par un petit C lorsqu'elle est rapportée à l'unité de masse (kg-1) et par un grand C lorsqu'elle est rapportée à une variation de température (joules par kelvin). Pour calculer l'énergie échangée par le glaçon, on utilise une formule classique qui relie l'énergie à la masse, la capacité calorifique massique et la variation de température du système. Cette formule peut également être exprimée comme la capacité calorifique du système multipliée par la variation de température. Dans le cas de notre glaçon, l'énergie échangée est égale à la masse du glaçon multipliée par la capacité calorifique massique de la glace, multipliée par la différence entre la température finale et la température initiale. En appliquant cette formule avec les valeurs données, nous obtenons une énergie échangée de -3,3 x 10^2 joules. Le signe négatif de cette énergie s'explique par le fait que le glaçon a cédé de l'énergie au système extérieur (le congélateur) en se refroidissant. En passant de -10°C à -18°C, le glaçon a perdu de l'énergie interne, d'où le signe négatif de l'énergie échangée. Ainsi, une énergie négative signifie que le système perd de l'énergie, tandis qu'une énergie positive indique que le système en reçoit. La compréhension de ce concept d'énergie échangée est importante en thermodynamique, il est donc recommandé de bien assimiler la formule et ses implications.

Se frotter les mains

Dans cette vidéo, Mathis du studio aborde l'efficacité du fait de se frotter les mains en hiver en utilisant des équations physiques. Il explique que la puissance de frottement est intégralement transmise à l'épiderme et utilise différentes données telles que l'épaisseur de l'épiderme, la surface de la paume de la main, la masse volumique de l'épiderme et la capacité thermique massique de l'épiderme pour déterminer la masse d'épiderme à chauffer. En utilisant la formule ρ × S × E, où ρ représente la masse volumique, S la surface de la peau de la main et E l'épaisseur de l'épiderme, il obtient une masse d'épiderme de 1,5 × 10-2 kg. Il poursuit en expliquant comment déterminer l'élévation de température lorsque l'on frotte ses mains pendant 60 secondes. Il relie la variation de température à une variation d'énergie à l'aide de la formule échangée : m × c × ΔT, où m est la masse d'épiderme à chauffer, c est la capacité thermique massique et ΔT est la variation de température. En utilisant la puissance de frottement et le temps pendant lequel on se frotte les mains (60 secondes), il obtient une variation de température de 19 degrés. Cependant, il souligne que cette valeur est surestimée en raison de l'hypothèse d'un système fermé, alors qu'en réalité une partie de l'énergie est dissipée dans l'air. En conclusion, il explique que cet exercice permet d'appliquer les lois apprises en physique, mais qu'il faut prendre en compte les hypothèses faites et la réalité du système.

Soupe miso

Dans cette vidéo, Matisse de Studio explique comment déterminer la température finale d'une soupe miso instantanée. Pour cela, on verse une masse d'eau de 150 grammes à une température initiale de 20 degrés. En considérant l'eau comme un système incompressible et en négligeant l'influence du contenu du sachet, on chauffe l'eau jusqu'à atteindre la température finale souhaitée, θF. Pour exprimer la variation d'énergie interne de l'eau en fonction de sa masse et de sa variation de température, on se réfère au mot-clé "exprimer", ce qui signifie qu'il faut donner une expression littérale plutôt que de déterminer la valeur numérique. Matisse rappelle l'importance de bien lire les énoncés en physique chimie. La relation de variation d'énergie interne en fonction de la variation de température est donnée par la masse d'eau chauffée fois sa capacité thermique massique, fois la variation de température. L'objectif est de calculer la température finale θF, étant donné que la variation d'énergie interne de l'eau δUiF doit être égale à 4,2 fois 10 puissance 4 joules. En utilisant les données disponibles (masse d'eau, capacité thermique massique et température initiale), on isole θF dans l'équation et on obtient que θF est égal à θI plus δUiF divisé par la masse d'eau fois sa capacité thermique massique. En effectuant le calcul numérique, on trouve que θF est égal à 87°C, ce qui est une température idéale pour une soupe miso instantanée. Matisse conclut l'exercice en soulignant l'importance de connaître par cœur l'expression de la variation d'énergie interne en fonction de la variation de température.

Gaz rare

Dans cette vidéo, nous abordons le sujet des gaz rares qui se trouvent dans la dernière colonne du tableau périodique. Les gaz rares comprennent l'hélium, le néon, l'argon, le krypton et le xénon. Ces gaz sont monoatomiques à l'état gazeux et se comportent comme des gaz parfaits. La question posée dans cette vidéo est de déterminer l'expression de la capacité thermique d'un gaz rare en considérant une variation de température ΔT. Pour répondre à cette question, nous devons poser un système thermodynamique et utiliser les données fournies. L'énergie interne d'une quantité N de gaz parfait monoatomique à une température T est donnée par U = 3,5NRT, où R est la constante des gaz parfaits. Pour exprimer la capacité thermique d'un gaz rare, nous devons diviser cette expression par ΔT. Donc, la capacité thermique d'un gaz rare est égale à 3,5NR. Ensuite, la vidéo se penche sur la question de la capacité thermique molaire des gaz rares, qui est égale à 12,47 joules par kelvin par mole. La capacité thermique molaire est la capacité thermique divisée par le nombre de moles de la substance. Dans ce cas, CM = C/N, où C est la capacité thermique du gaz rare. En conclusion, cette vidéo explique comment déterminer l'expression et la valeur numérique de la capacité thermique d'un gaz rare en utilisant des concepts de thermodynamique.

Étude d’un gaz

Dans cette vidéo, Matisse de Studio explique l'étude d'un gaz. On place le gaz dans une enceinte incompressible et indilatable, entourée d'un milieu ambiant à température T0. Les variables d'état initiales du gaz sont N1, T1, P1 et V1, et à l'équilibre thermique ces variables deviennent N2, T2, P2 et V2. La première question concerne la condition pour atteindre l'équilibre thermodynamique, qui est que T2 soit égal à T0. Ensuite, en utilisant l'équation d'état d'un gaz parfait, on peut déterminer les valeurs de N2, T2, P2 et V2. Enfin, la troisième question porte sur la condition pour que l'énergie Q échangée par le gaz soit positive. Selon la première loi de la thermodynamique, l'énergie échangée est égale à moins la variation d'énergie interne du système. Donc, si T1 est strictement supérieur à T0, l'énergie échangée sera positive, ce qui signifie que l'enceinte cèdera de l'énergie au milieu extérieur. Cette vidéo présente une approche intéressante en thermodynamique, en partant d'un système initial pour calculer les nouvelles grandeurs d'état après des transformations.

Étude d’un réfrégirateur

Dans cette vidéo, on étudie le fonctionnement d'un réfrigérateur selon la méthode des machines thermiques. On utilise un schéma pour représenter les grandeurs Qc, Qf et W, ainsi que les sources chaudes et froides. Le réfrigérateur utilise un fluide frigorigène pour absorber la chaleur à l'intérieur et la restituer à l'extérieur. Le compresseur fournit le travail mécanique nécessaire, généralement sous forme d'énergie électrique. La source chaude est l'extérieur, où le fluide frigorigène transfère de l'énergie thermique. La source froide est l'intérieur du réfrigérateur, d'où l'énergie est prélevée. Les grandeurs Qc, Qf et W sont définies comme étant l'énergie reçue par le fluide frigorigène. La valeur positive de W signifie que le compresseur fournit de l'énergie mécanique au fluide. La valeur positive de Qf indique que le réfrigérateur transfère de l'énergie au fluide frigorigène. Au contraire, la valeur négative de Qc représente l'énergie que le réfrigérateur cède au milieu extérieur. La vidéo souligne également l'importance de comprendre ces grandeurs algébriques pour pouvoir mener une étude approfondie des systèmes thermodynamiques.

BAC : Cogénération

La vidéo porte sur la co-génération, qui est la production simultanée d'énergie électrique et d'énergie thermique à partir d'un combustible dans un co-générateur. On nous présente ensuite le cas de l'exploitation agricole GAEC des Châtelet, qui a développé une structure de méthanisation co-génération en 2009. Les caractéristiques techniques de ce co-générateur sont données, incluant sa puissance électrique, sa production annuelle d'énergie thermique et électrique, ainsi que son efficacité énergétique globale. Les besoins de l'agriculteur en eau chaude sont également mentionnés. Ensuite, le cours propose des calculs pour déterminer la quantité d'énergie libérée par la combustion du biogaz dans l'installation, ainsi que le volume de biogaz correspondant. Il explique également comment calculer le volume d'eau pouvant être chauffé grâce à l'énergie thermique produite par l'installation. Enfin, le cours justifie que l'eau chaude produite peut être utilisée à la fois pour la salle de traite et pour d'autres usagers. Il suggère l'ajout d'un réseau de distribution pour bénéficier de cette énergie. Voilà un résumé du cours en SEO friendly.

BAC : Vol en montgolfière

Dans cette vidéo, Matisse de Studio explique comment faire décoller une montgolfière. Il commence par modéliser une montgolfière par un ballon rigide dont le volume est constant, avec une ouverture à la base permettant à l'air de rentrer ou de s'échapper. Le ballon contient de l'air à 20 degrés et à une pression de 1,013 x 10,5 pascal. Il explique ensuite que l'air est composé en volume de 80% de diazote N2 et de 20% de dioxygène O2. La masse molaire de l'air est égale à la somme des masses molaires du diazote et du dioxygène, coefficientées par leur pourcentage volumique. La masse molaire de l'air est ainsi de 28,8 grammes par mole. Il rappelle ensuite les conditions pour qu'un gaz puisse être assimilé à un gaz parfait, c'est-à-dire que les interactions entre les molécules au sein du gaz sont négligées. Il calcule ensuite la quantité de matière d'air présente dans le ballon en utilisant l'équation d'état des gaz parfaits, ce qui donne une quantité de matière de 0,42 mol. Il calcule ensuite la masse de l'air compris dans le ballon en utilisant la formule masse de l'air = quantité de matière * masse molaire de l'air, ce qui donne une masse de 12 g. Il explique ensuite que la pression de l'air dans le ballon reste inchangée lorsque la température change, car le volume du ballon reste constant. Il calcule ensuite la masse de l'air qui s'est échappée du ballon en utilisant l'équation d'état des gaz parfaits avec la nouvelle température de 90°C, ce qui donne une masse d'air échappée de 2,3 g. Il explique ensuite que le décollage de la montgolfière dépend de deux forces, son poids et la poussée d'Archimède. Il utilise la deuxième loi de Newton et projette les forces sur l'axe vertical pour déterminer les conditions dans lesquelles la montgolfière peut décoller. Enfin, il montre que l'air à l'intérieur du ballon doit être chauffé jusqu'à une certaine température pour que le décollage ait lieu. Il utilise une analyse thermodynamique et mécanique pour le démontrer. Il conclut en encourageant les spectateurs à revoir l'exercice, qui est complet et représente un exercice typique de niveau Bac. Il précise que la dernière partie peut être complexe à comprendre, mais il souligne l'importance de bien saisir la notion de poussée d'Archimède et la comparaison entre l'air chauffé et non chauffé. Il termine en montrant que la montgolfière a besoin de chauffer l'air à l'intérieur pour décoller.

Schéma de Bernoulli

Le cours porte sur la reconnaissance et l'utilisation de la loi binomiale. Pour cela, il est nécessaire de suivre deux étapes principales. Tout d'abord, il faut identifier un chemin de Bernoulli, qui est une expérience répétée plusieurs fois de manière indépendante, et qui comporte deux résultats possibles (succès ou échec). Ensuite, il faut attribuer une variable aléatoire x qui représente le nombre de succès. Cette variable suit une loi binomiale avec les paramètres n (nombre de répétitions) et p (probabilité de succès). La formule utilisée pour calculer la probabilité que x soit égal à k est k parmi n fois p à la puissance k, multiplié par 1 moins p à la puissance n moins k. Dans l'exemple donné, il s'agit de tirages successifs et indépendants de boules noires. Le paramètre est de 3 boules noires sur 8 boules, soit une probabilité de réussite de 3 huitièmes. La variable x, qui compte le nombre de boules noires obtenues, suit donc une loi binomiale avec n égal à 5 et p égal à 3 huitièmes. En effectuant les calculs, on trouve une probabilité de 20% pour x égal à 3. C'est ainsi qu'on reconnaît et utilise la loi binomiale. Pour plus d'informations, consultez la FAQ.

Calcul brut de probabilités

Dans ce cours, nous commençons à effectuer les premiers calculs avec la loi binomiale. Pour cela, nous avons besoin d'une calculatrice. La loi binomiale que nous utilisons a un grand X qui suit la loi avec les paramètres n = 50 et p = 0,23. Nous devons calculer trois probabilités. La première probabilité est que p soit strictement inférieur à 12, ce qui est équivalent à la probabilité que x soit inférieur ou égal à 11. Cette donnée peut être obtenue sur toutes les calculatrices graphiques du lycée. En utilisant la calculatrice, nous obtenons un résultat de 0,512. Si nous n'avons pas de calculatrice, il faudrait faire la somme des probabilités de x égale à 1, plus la probabilité de x égale à 2, etc., jusqu'à x égale à 11. Cependant, cela serait fastidieux. C'est pourquoi lorsque nous vous posons cette question, vous avez le droit d'utiliser la calculatrice. Nous aurions également pu vous demander une probabilité sans calculatrice, telle que p de x inférieur à 3. Faire la somme de trois probabilités n'est pas non plus compliqué. Pour la probabilité que x soit supérieur ou égal à 4, je considère plutôt l'événement contraire, qui est l'événement contraire de x inférieur ou égal à 3. Nous pouvons calculer cette probabilité en utilisant 1 moins la probabilité de x inférieur à 3. En utilisant la calculatrice, nous obtenons un résultat de 0,999. Ensuite, nous devons calculer la probabilité que x soit compris entre 5 et 8. Cela revient à calculer la différence entre x inférieur ou égal à 8 et x inférieur ou égal à 5. En utilisant la calculatrice, nous obtenons un résultat. Une autre méthode consiste à considérer que x compris entre 5 et 8 signifie qu'il peut prendre les valeurs 6 ou 7. Nous pouvons donc ajouter les probabilités de x égale à 6 et x égale à 7, ce qui donne un résultat de 0,14. Heureusement, les deux méthodes donnent le même résultat. C'est tout pour les calculs avec la loi binomiale en utilisant la calculatrice. Il suffit de s'assurer que vous connaissez la bonne fonction à utiliser, ce qui est assez facile à trouver. Vous pouvez demander à vos camarades, consulter la FAQ de votre modèle de calculatrice ou chercher sur Google. Les trois méthodes fonctionnent.

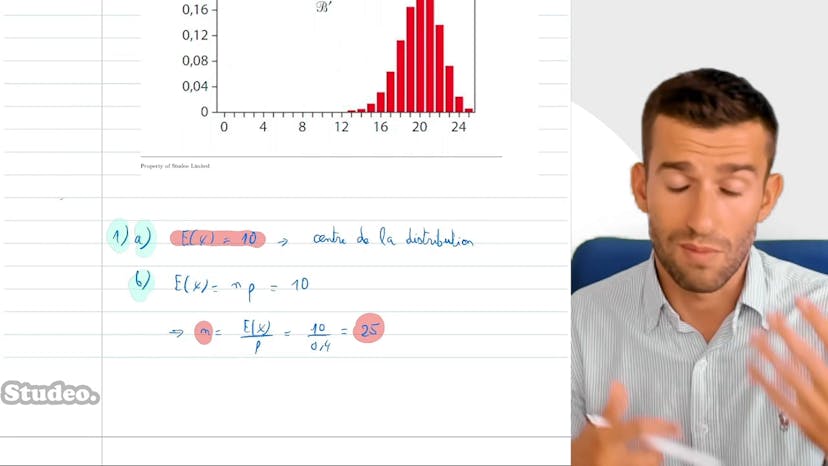
Espérance et écart-type : graphique

Dans ce cours, nous apprenons comment utiliser les diagrammes en barre pour les lois binomiales. Dans le premier exemple, nous avons une loi binomiale avec une probabilité de succès de 0,4, mais nous ne connaissons pas la valeur de N. Nous devons estimer l'espérance. La loi binomiale n'est symétrique que lorsque la probabilité est de 0,5, donc nous estimons que l'espérance est centrée autour de 10. En utilisant la formule de l'espérance (E2x), nous estimons que N est égal à 25. Dans le deuxième exemple, nous devons comparer deux lois binomiales. Nous remarquons que l'une est plus recentrée que l'autre, ce qui signifie que son écart-type est plus faible. L'écart-type mesure l'écart à la moyenne, et plus il est élevé, plus les valeurs sont loin de l'espérance. Les valeurs importantes à retenir sont l'espérance (NxP), la variance (NPx-P), et l'écart-type (racine carrée de la variance). Enfin, dans un exercice supplémentaire, nous cherchons à déterminer quelle valeur de P est la plus faible. En utilisant la fonction f2x égale à x fois 1-x, nous trouvons que l'écart-type maximum est atteint lorsque la probabilité vaut 1,5. Cela est dû au fait qu'il y a autant de chances d'échec que de réussite, ce qui peut entraîner des résultats très différents. En résumé, ce cours explique comment utiliser les diagrammes en barre pour les lois binomiales, estimer l'espérance et comparer différentes lois binomiales en fonction de leur écart-type.