Cours d'apprentissage en ligne

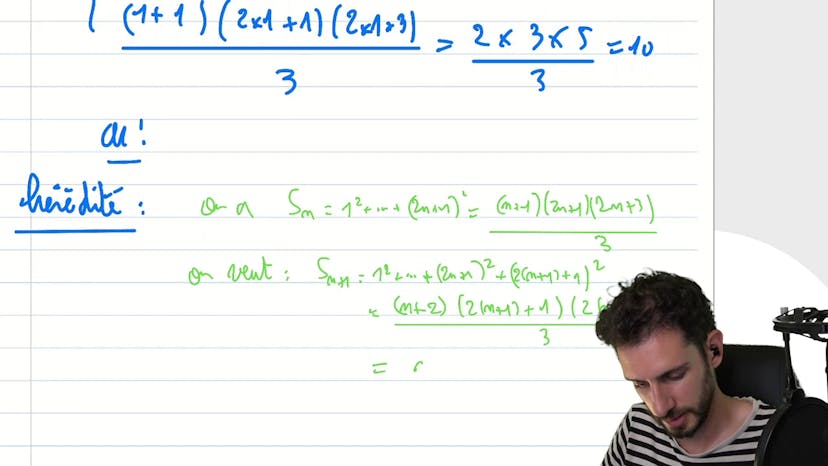
Avec une Somme

Ce cours est une transcription d'une vidéo qui explique l'importance d'écrire clairement et précisément en mathématiques. L'exemple donné est la démonstration par récurrence d'une formule mathématique. Le professeur utilise des notations et des termes spécifiques pour expliquer le processus de rédaction d'une démonstration mathématique. Il insiste sur la nécessité de suivre les consignes du professeur et de montrer clairement chaque étape du raisonnement. Le professeur utilise également des astuces pour simplifier les calculs, comme factoriser ou utiliser des notations abrégées. La conclusion est que la rédaction soignée et précise est essentielle pour éviter les erreurs et faciliter la compréhension des démonstrations mathématiques.

Majoration 'simple'

Ce cours est une transcription d'une vidéo qui traite de la démonstration par récurrence. L'objectif est de montrer que pour toute valeur de n appartenant à n étoiles, la propriété est vraie. La démonstration commence par l'initialisation avec n=1, où l'on obtient S1=1. Ensuite, on utilise l'hérédité en supposant que la propriété est vraie pour un certain n et en démontrant qu'elle est aussi vraie pour n+1. On utilise une inégalité pour montrer que Sn+1 est inférieur ou égal à 2-1/n+1. En utilisant des manipulations algébriques, on montre que l'inégalité est vraie et donc que la propriété est héréditaire. En conclusion, on peut affirmer que la propriété est démontrée pour tout n appartenant à n étoiles. Cependant, il est important d'écrire une conclusion pour éviter de perdre des points lors de l'évaluation.

Trop de puissance !

Ce cours concerne une suite définie par un terme initial u0 et une relation de récurrence. Le processus pour calculer les termes de la suite consiste en deux étapes : d'abord avoir une intuition du résultat en calculant u1, u2, u3, etc., puis démontrer cette intuition par récurrence. Pour cela, on écrit une formule générale basée sur les premiers termes de la suite et on la démontre. Dans cet exemple, on montre que la suite est égale à u0 puissance 2 puissance n. On commence par l'initialisation avec n=0, où la formule se simplifie à u0. Ensuite, on utilise la récurrence pour démontrer que Pn implique Pn+1. La démonstration de la récurrence dans cet exemple est assez simple, mais il est important de comprendre la méthode générale pour résoudre ce type d'exercice, en utilisant des intuitions, des essais de premiers termes et des démonstrations par récurrence. Ces compétences seront utiles non seulement pour le supérieur, mais aussi pour le bac.

Majoration plus costaude

Ce cours est une transcription d'une vidéo sur les démonstrations récursives en mathématiques. Il aborde les concepts de récurrence, d'initialisation et d'hérédité, ainsi que les manipulations des équations trigonométriques. L'orateur insiste sur l'importance de connaître les formules et d'être capable de poser les bonnes questions pour résoudre les problèmes mathématiques.

Intro Suites et limites

Dans cette vidéo, on aborde le sujet des limites de suite. Une limite de suite est lorsque les valeurs d'une suite tendent vers une valeur spécifique. Un exemple est donné où une suite augmente et finit par se stabiliser autour d'une certaine valeur, ce qui suggère qu'elle tend vers une limite. Cependant, les mathématiciens préfèrent des définitions formelles qui peuvent sembler complexes, mais l'objectif est de les rendre plus accessibles en se référant aux graphiques correspondants. On compare ensuite ce sujet à l'étude de la dérivée en mathématiques, où au début, on utilise des définitions formelles puis on utilise des tables de dérivées classiques pour simplifier le processus. De la même manière, pour les limites de suite, il y a des définitions formelles à connaître, mais aussi des tableaux de limites classiques qui seront utiles. Le cours se divise en trois parties principales. La première porte sur la définition de la limite pour l'infini positif, l'infini négatif et une valeur réelle spécifique. On aborde également la propriété d'unicité de la limite. La deuxième partie concerne les limites de référence et les opérations possibles sur les limites. Des tableaux de limites classiques sont présentés. Enfin, la troisième partie aborde les limites des suites géométriques, avec un rappel sur la somme des termes d'une suite géométrique et les cas où cette somme peut avoir une limite. Quatre principales méthodes sont présentées. La première consiste à appliquer la définition formelle des limites dans certains exercices. Les deuxième et troisième méthodes sont basées sur les limites de référence et les opérations sur les limites, qui permettent de prédire certaines limites ou de résoudre les cas plus complexes. Enfin, une méthode rappelant la somme des termes d'une suite géométrique est également abordée. La vidéo se termine en encourageant les spectateurs à poser des questions dans la FAQ et en annonçant une prochaine vidéo sur le sujet.

Limite finie

Dans cette première vidéo sur les limites en mathématiques, nous allons aborder la notion de limite réelle. La limite réelle correspond à la valeur vers laquelle une suite converge intuitivement lorsque n augmente. Pour une meilleure précision, nous utilisons la notion de couloir en mathématiques. Dans cette vidéo, nous allons donc expliciter l'idée de couloir autour de la limite et montrer que la convergence peut se faire de manière progressive (croissante ou décroissante) mais aussi de manière plus chaotique. La définition officielle de la limite nous dit que si une suite UN converge vers un réel L, alors tous les termes de la suite seront inclus dans n'importe quel intervalle autour de L à un certain moment. Pour mieux comprendre cette définition, nous allons utiliser un graphique. Nous prenons une suite et nous choisissons un intervalle autour de la limite supposée. Si, à partir d'un certain moment, tous les termes de la suite sont inclus dans cet intervalle, alors nous pouvons dire que la limite est correcte. En d'autres termes, plus nous réduisons la taille de l'intervalle, plus les termes de la suite convergent vers la limite choisie. Nous pouvons illustrer cela avec différents exemples de suites convergentes. Nous pouvons prendre une suite croissante, une suite décroissante ou même une suite oscillante. Dans tous les cas, si tous les termes de la suite sont inclus dans un intervalle autour de la limite, alors nous pouvons dire que la limite est correcte. En conclusion, dans cette première vidéo, nous avons expliqué la notion de limite réelle en utilisant la notion de couloir. Nous avons montré que la convergence peut se faire de différentes manières (croissante, décroissante ou oscillante) tant que tous les termes de la suite sont inclus dans un intervalle autour de la limite. Dans la prochaine vidéo, nous approfondirons davantage ces notions. N'hésitez pas à poser vos questions dans la FAQ.

En l'infini

Dans cette vidéo, l'enseignant aborde la notion de limite infinie. Il explique que lorsqu'une suite tend vers l'infini, cela signifie que pour n'importe quelle valeur seuil, il est possible de trouver un rang à partir duquel tous les termes de la suite seront supérieurs à cette valeur seuil. Il illustre cette notion avec un graphique représentant une suite croissante basée sur la parabole x^2. Il montre que peu importe la valeur seuil choisie, il existe un rang à partir duquel tous les termes de la suite sont supérieurs à cette valeur. Il mentionne également que la notion de limite infinie est symétrique, c'est-à-dire qu'une suite tend vers moins l'infini si tous ses termes sont inférieurs à n'importe quelle valeur seuil négative. Il propose également de poser des questions dans la FAQ si besoin et annonce la prochaine vidéo. Ce résumé met l'accent sur les notions clés du cours, en utilisant des phrases simples et courtes pour optimiser la convivialité du référencement.

Unicité et Divergence

Dans cette vidéo, nous approfondissons notre compréhension de la convergence et des limites dans le contexte des suites. Le premier point important est que lorsque nous avons une limite finie, elle est unique. En d'autres termes, si nous nous approchons d'une valeur, nous ne pouvons nous approcher que d'une seule valeur. Cela est intuitif et facile à comprendre. Le deuxième point concerne le vocabulaire. Nous utilisons le terme "convergence" pour décrire une suite lorsque nous avons une limite finie. Cependant, il est crucial de comprendre que ne pas converger ne signifie pas automatiquement tendre vers l'infini positif ou négatif. Il est possible de ne pas converger différemment. 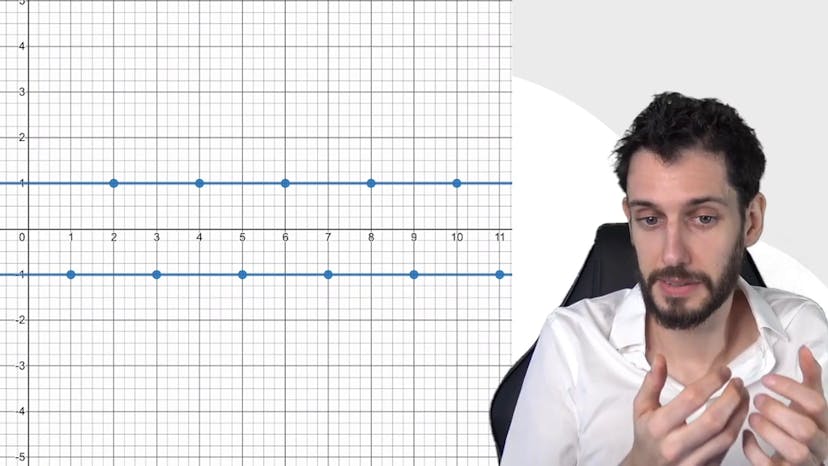Il existe un cas spécifique de divergence appelé "oscillation". Par exemple, prenons la suite (-1) élevé à la puissance n. Elle vaut 1 lorsque n est égal à 0, -1 lorsque n est égal à 1, 1 lorsque n est égal à 2, et ainsi de suite. Cette suite oscille entre -1 et 1, donc elle ne converge ni vers -1 ni vers 1, et n'a pas de limite finie. Cependant, elle ne tend pas non plus vers l'infini positif ou négatif. Elle présente simplement un comportement d'oscillation permanent. Il est important de mentionner que l'existence de petites convergences pour certains termes de la suite ne signifie pas une convergence globale de toute la suite. C'est un concept plus avancé qui va au-delà du programme scolaire et implique l'extraction de sous-suites à partir de suites plus générales. Dans l'exemple précédent, on pourrait extraire les termes "en haut" de la suite et dire qu'ils tendent vers 1. Cependant, pour la suite dans son ensemble, il n'y a pas de limite, pas de tendance vers l'infini positif ou négatif. Ainsi, nous avons exploré différentes possibilités de convergence et de divergence des suites. Si vous souhaitez plus de détails ou des informations supplémentaires, n'hésitez pas à consulter notre FAQ ou à nous contacter. À bientôt !

Limites de référence et opérations

Dans ce cours, nous avons étudié les limites de suites et avons appris quelques outils pratiques qu'il est important de connaître dans le programme de mathématiques. Tout d'abord, nous avons vu que les puissances de n tendent vers plus l'infini lorsque n tend vers plus l'infini. Cela s'applique non seulement aux puissances entières de n, mais aussi aux racines de n. Ainsi, on peut dire que les puissances positives de n, quel que soit l'entier k ou le nombre rationnel, tendent vers plus l'infini. De plus, il est important de noter que plus la puissance augmente, plus la suite tend vers plus l'infini rapidement. Par exemple, n³ croît plus rapidement que n². Ensuite, nous avons abordé les puissances négatives de n, c'est-à-dire 1/n. Dans ce cas, la suite tend vers zéro, car 1 divisé par un nombre très grand devient très petit. Ainsi, toutes ces fonctions tendent vers 0. Nous avons également étudié comment gérer les opérations sur différentes suites. Par exemple, si nous connaissons les limites de deux suites, pouvons-nous en déduire la limite de leur somme ? Dans la plupart des cas, la réponse est oui. En effet, si une suite tend vers l et une autre tend vers l', alors leur somme tend vers l + l'. Si l'une tend vers plus ou moins l'infini et l'autre vers une limite finie, c'est l'infini qui l'emporte. De même, si les deux tendent vers plus ou moins l'infini, le résultat sera également plus ou moins l'infini. Cependant, lorsque la limite est une forme indéterminée, il n'y a pas de règle prédéterminée à suivre. Il faut donc évaluer chaque cas individuellement. Enfin, nous avons mentionné deux autres formes indéterminées à connaître : le produit de deux suites, où l'une tend vers zéro et l'autre vers l'infini, ainsi que le quotient de deux suites, où l'une tend vers l'infini et l'autre vers zéro. Il est important de reconnaître ces formes indéterminées car elles nécessitent une méthode spécifique pour les résoudre. En conclusion, il est essentiel d'apprendre et de mémoriser les tables des limites des suites, ainsi que de comprendre les quatre formes indéterminées mentionnées : plus l'infini, moins l'infini, zéro fois plus l'infini et zéro fois l'infini en négatif, et le quotient de l'infini sur l'infini ou le quotient de zéro sur zéro. En connaissant ces concepts, vous serez prêt à résoudre des exercices sur les limites de suites.

Suites géométriques - illustration

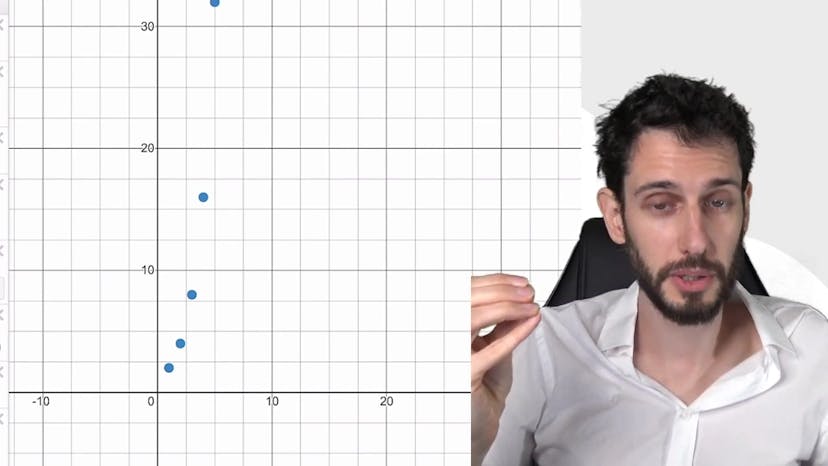
Ce cours explique les différents comportements des suites géométriques en fonction de la valeur de la raison, Q. Lorsque Q est plus grand que 1, la suite converge vers l'infini. Par exemple, si Q équivaut à 3, la suite augmente de plus en plus avec chaque terme. Ce comportement peut être démontré à l'aide de l'inégalité de Bernoulli. Lorsque Q est compris entre -1 et 1, la suite converge vers 0. Par exemple, si Q équivaut à 0,5, chaque terme devient de plus en plus petit, et à l'infini, il reste seulement 0. Ce comportement s'explique par le fait que chaque terme est une fraction de plus en plus petite du terme précédent. Si Q équivaut à 1, la suite converge simplement vers 1, ce qui est un cas trivial. En revanche, lorsque Q est inférieur à -1, la suite diverge, mais d'une manière plus complexe. Elle oscille autour de 0 en s'écartant tantôt vers le positif, tantôt vers le négatif. Ce comportement est illustré graphiquement en montrant les termes successifs de la suite. Pour résumer, lorsque la raison est proche de 0, la suite converge progressivement vers 0, que ce soit de manière oscillante ou non. Lorsque la raison est plus grande que 1 ou plus petite que -1, la suite s'écarte de 0, soit vers l'infini, soit de manière plus complexe. Ce cours prépare à une prochaine vidéo qui démontrera ces comportements.

Suites géométriques : démo

Dans cette vidéo, nous démontrons les intuitions graphiques sur la limite des suites géométriques. Il y a plusieurs cas à démontrer. Dans le premier cas, lorsque Q est strictement supérieur à 1, nous démontrons que Q élevé à la puissance n tend vers l'infini. Pour cela, nous utilisons l'inégalité de Bernoulli et le terrain de comparaison. En posant Q = 1+h, avec h positif, nous appliquons l'inégalité de Bernoulli pour écrire que 1+h élevé à la puissance n est supérieur ou égal à 1+nh. Comme 1+nh est une suite arithmétique de raison positive qui tend vers l'infini, le terrain de comparaison nous permet d'affirmer que Q élevé à la puissance n tend vers l'infini. Les autres cas se rapportent au cas précédent. Par exemple, lorsque Q est entre 0 et 1, nous posons P = 1/Q et utilisons le résultat précédent pour dire que P élevé à la puissance n tend vers l'infini. Il en découle que Q élevé à la puissance n tend vers 0. Dans le dernier cas, nous appliquons le théorème des gendarmes pour encadrer la suite Q élevé à la puissance n entre deux suites qui convergent vers 0. Ainsi, Q élevé à la puissance n tend également vers 0. Les deux autres cas sont de simples astuces pour éviter de faire trop d'efforts lors de la démonstration. La démonstration des trois formules est assez rapide, avec un cas particulièrement fort lorsque Q est plus grand que 1. Les deux autres cas sont des façon astucieuses de réutiliser des résultats précédents. Cette démonstration doit être connue par cœur dans le programme. N'hésitez pas à poser vos questions dans la FAQ et je vous retrouve dans la prochaine vidéo.