 Tous les sujets
Tous les sujets Maths
Maths Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée Prépa Examens
Prépa Examens
Terminale
Première
Seconde
MPSI/PCSI
2BAC SM Maroc
 Tous les sujets
Tous les sujets Maths
Maths Physique-Chimie
Physique-Chimie Corrigés de BAC
Corrigés de BAC Révisions Maths lycée
Révisions Maths lycée Prépa Examens
Prépa Examens
Révisions Maths lycée
Analyse Terminale
MPSI/PCSI

Forme indéterminée : Méthode quantité conjuguée
La méthode de la quantité conjuguée est une technique classique utilisée lorsque nous avons des racines dans une équation. Lorsque nous ne voulons pas effectuer les calculs avec les racines car elles ne s'additionnent pas facilement, nous pouvons utiliser la quantité conjuguée pour les éliminer.
Nous avons ici un exemple de fonction avec une forme indéterminée lorsque x tend vers 0. Cependant, lorsque x tend vers 0, le terme en question tend vers 1 et la racine de x tend vers 0, ce qui donne 1 sur 1. Donc pour x > 0, il n'y a pas de problème, cela tend vers 1. La racine de x n'étant pas définie pour les valeurs négatives, nous nous concentrons sur les valeurs positives.
En revanche, lorsque x tend vers l'infini, la situation est différente. Sans effectuer de calculs détaillés, nous pouvons voir que cela donne plus l'infini moins l'infini, ce qui est une forme indéterminée. Les racines ne se factorisent pas facilement entre elles, donc nous utilisons la quantité conjuguée. En multipliant le numérateur et le dénominateur par la quantité conjuguée, les racines disparaissent en bas mais apparaissent en haut. Cependant, cela est avantageux car cela transforme le signe moins en un signe plus, ce qui résout le problème de l'indétermination.
Ainsi, nous obtenons x plus 1 moins x au dénominateur, ce qui simplifie à x plus 1. Finalement, le dénominateur devient 1 et la fonction devient la somme de deux racines de x, ce qui n'est plus une forme indéterminée. Donc, lorsque les racines diffèrent, il est conseillé d'utiliser la quantité conjuguée car cela élimine automatiquement l'indétermination. Voilà donc l'utilité de cette méthode classique pour les limites avec racines.
Révisions Maths lycée
Analyse Terminale
MPSI/PCSI

Limites : la Croissance comparée
La méthode de la croissance comparée est une technique très utile en mathématiques. Elle consiste à comparer la croissance de différentes fonctions pour déterminer le comportement de ces fonctions lorsque la variable tend vers l'infini ou moins l'infini.
Dans cette transcription, l'auteur utilise cette méthode pour étudier deux fonctions, e de x sur x et x puissance 4 sur e de x.
Pour la première fonction, e de x sur x, il montre que lorsque x tend vers moins l'infini, la fonction tend vers 0, car e de x tend vers 0 et x sur moins l'infini est toujours égal à 0. Lorsque x tend vers plus l'infini, il dit que par croissance comparée, e de x l'emporte sur toute puissance de x et donc la fonction tend vers plus l'infini.
Pour la deuxième fonction, x puissance 4 sur e de x, l'auteur fait un changement de variable astucieux en posant grand x égal à moins l'infini plus petit x. Ainsi, il peut écrire x sur e de x comme l'inverse de la croissance comparée de référence, qui tend vers 0. Par composition des limites, il conclut que la fonction tend vers 0.
En résumé, la méthode de la croissance comparée permet de déterminer le comportement de fonctions lorsque la variable tend vers l'infini ou moins l'infini. Grâce à cette méthode, on peut conclure que e de x sur x tend vers plus l'infini lorsque x tend vers plus l'infini, et que x puissance 4 sur e de x tend vers 0 lorsque x tend vers moins l'infini. Cette méthode est utile pour lever rapidement la détermination dans des calculs mathématiques.
Révisions Maths lycée
Analyse Terminale
MPSI/PCSI

Double racine
Bonjour à tous, dans cet exercice sur les limites, nous devons montrer que la fonction f est définie sur l'ensemble des réels. Pour cela, nous examinons les racines de la fonction. Pour la première racine, nous remarquons que x² et 1+x² sont toujours strictement positifs, donc il n'y a pas de problème. En ce qui concerne la deuxième racine, nous devons faire deux cas : si x > 0, alors x est positif et 1+x² est positif, donc pas de problème. Si x < 0, nous comparons les deux termes et remarquons que 1+x² est plus grand que x², donc racine(1+x²) est bien défini et positif. Ainsi, les racines sont définies pour tout x appartenant à R, donc l'ensemble de définition de f est R.
Pour la deuxième question, nous devons justifier que f est dérivable sur tout R. Pour cela, nous devons montrer que l'intérieur des racines est strictement positif. En utilisant les inégalités précédentes, nous pouvons conclure que l'intérieur des racines est strictement positif pour tout x. Nous justifions également que la fonction racine est dérivable en 0, car nous avons déjà montré que son intérieur est strictement positif. Donc, f est dérivable sur R.
Ensuite, nous calculons la dérivée de f en utilisant la composition et les formules de dérivation. Nous obtenons une expression pour f'(x) qui est toujours strictement positive. Donc, f est strictement croissante sur R.
Nous passons ensuite à l'étude des limites. La limite de f lorsque x tend vers plus l'infini est plus l'infini, ce que nous justifions en composant avec la limite de racine. La limite de f lorsque x tend vers moins l'infini est 0, ce que nous démontrons en utilisant la quantité conjuguée. Ainsi, nous concluons que la limite de f lorsque x tend vers plus l'infini est plus l'infini et la limite de f lorsque x tend vers moins l'infini est 0.
Enfin, nous traçons le graphique de f en utilisant des valeurs remarquables. Nous vérifions que f tend vers moins l'infini lorsque x tend vers 0 et que f tend vers plus l'infini lorsque x tend vers plus l'infini.
C'était la correction de cet exercice sur les limites. N'hésitez pas à poser vos questions dans la FAQ. Merci !
Révisions Maths lycée
Analyse Terminale
MPSI/PCSI
Calculs de limites complexes
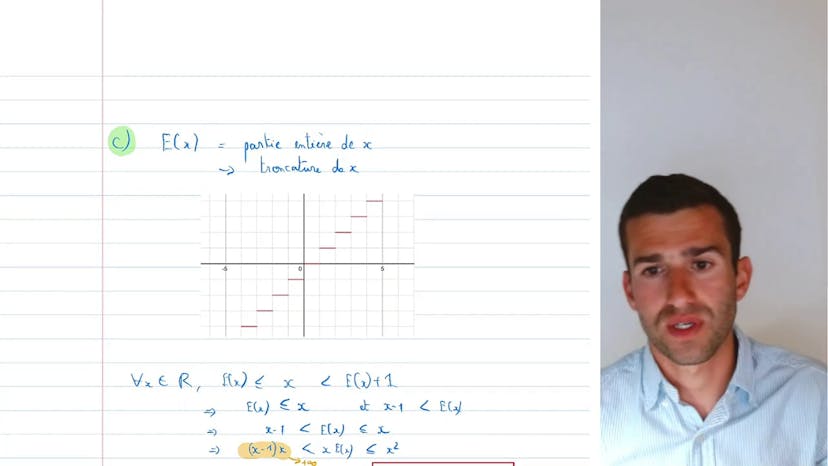
Bonjour à tous, aujourd'hui nous allons étudier des exercices avancés sur les limites. Ce cours s'adresse principalement à ceux qui souhaitent se préparer pour l'année prochaine. Le premier exemple concerne les racines. Lorsque l'on rencontre des racines dans un exercice, il faut penser à utiliser la quantité conjuguée. Dans cet exemple, nous avons une forme d'indétermination avec des racines infinies. En utilisant la quantité conjuguée, nous pouvons simplifier l'expression et trouver la limite de la fonction. Dans le deuxième exemple, nous avons une expression avec des puissances. En utilisant la dérivée, nous pouvons simplifier l'expression et trouver la limite de la fonction. Le troisième exemple concerne la partie entière. En utilisant des encadrements, nous pouvons déterminer la limite de la fonction. Le quatrième exemple est similaire au premier, avec de nombreuses racines. En utilisant la quantité conjuguée et des simplifications, nous pouvons trouver la limite de la fonction. En résumé, ces exemples montrent différentes techniques pour calculer des limites dans des expressions complexes.
Révisions Maths lycée
Analyse Terminale
MPSI/PCSI
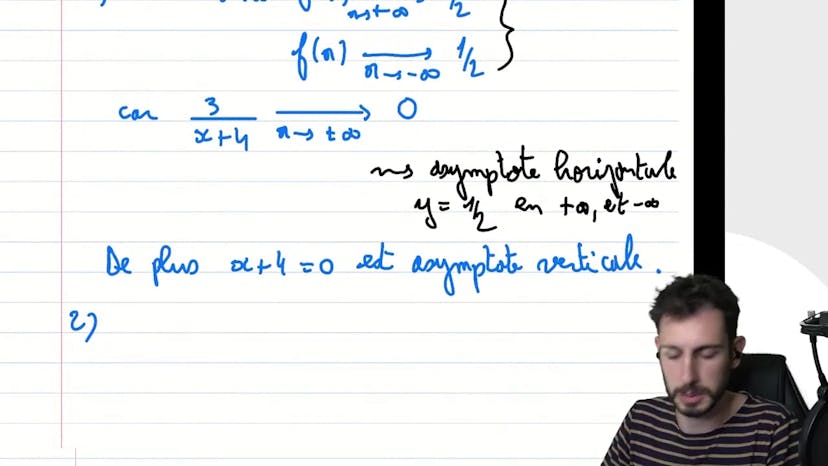
Asymptote et position relative
Ce cours est une transcription d'une vidéo qui traite de l'étude de fonctions, notamment l'étude d'asymptotes et de positions relatives. Le professeur commence par dire que l'exercice choisi est une fonction classique et qu'il souhaite rappeler les réflexes à avoir pour bien le maîtriser. Il fait remarquer que lorsqu'on voit f(x) écrit comme f2x, il faut immédiatement factoriser. Il explique que lorsqu'on étudie les limites en plus ou moins l'infini, on peut considérer que les constantes à côté de x n'ont pas d'importance. Ainsi, il simplifie rapidement la fonction en x/2x, ce qui donne 1,5. Ensuite, il aborde la réécriture des fonctions inverses, en manipulant le numerator pour que le denominator soit égal à x+4. Il sépare alors la fraction en deux et obtient une expression plus pratique à travailler. Cette écriture permet de répondre rapidement à la question 1, en identifiant les asymptotes horizontales et verticales. Ensuite, il explique que l'expression simplifiée de la fonction facilite également la réponse à la question 2, en trouvant la position relative de la fonction par rapport à l'asymptote horizontale. Il conclut en insistant sur l'importance d'intuiter et de repérer rapidement les asymptotes et les limites pour bien étudier une fonction.
Révisions Maths lycée
Analyse Terminale
MPSI/PCSI
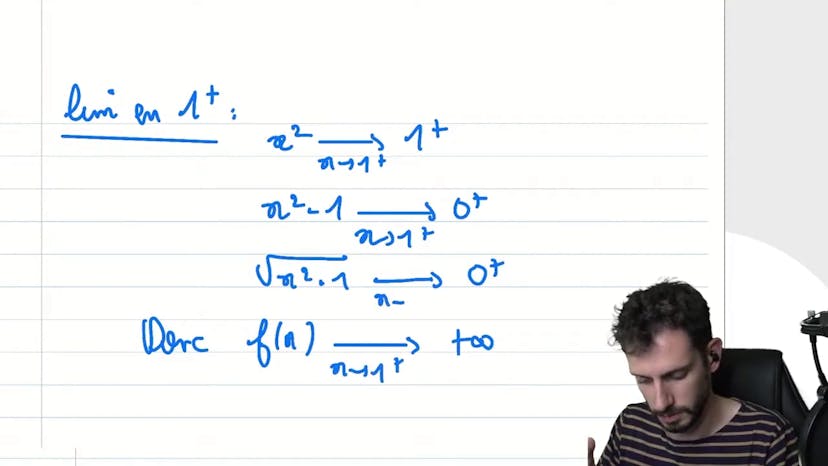
Étude TRES complète
Il est important d'écrire en français ce que vous voulez faire, car une racine n'est définie que pour des nombres positifs ou nuls sur R+. Donc, il faut que ce qu'il y a sous la racine soit positif ou nul. En gros, cela signifie que x doit être supérieur à 1 ou inférieur à -1.
En plus de cela, la fonction est définie comme un quotient, donc il faut également s'assurer que la racine de x²-1 soit différente de 0 pour éviter de diviser par 0.
Pour trouver les limites, nous pouvons utiliser deux étapes. Cependant, il est important de ne pas seulement exclure les valeurs -1 et 1, car cela ne fonctionne pas dans tous les cas. Par exemple, si nous prenons x = 0.5, nous obtenons un résultat négatif, ce qui ne fonctionne pas.
L'ensemble de définition (DF) de la fonction comprend quatre bornes. Il est important de faire attention à celles-ci.
Il est également utile de vérifier si la fonction est impaire ou paire, car cela peut réduire le travail à effectuer. Si la fonction est impaire, cela signifie que la courbe de la fonction possède un point de symétrie au point O. Par conséquent, si nous comprenons comment la fonction évolue de 0 à l'infini, nous pouvons automatiquement déduire son évolution de moins l'infini à 0.
Maintenant, passons aux calculs des limites. Nous commencerons par les limites de droite, c'est-à-dire 1 par la droite et l'infini. Lorsque x tend vers l'infini, x²-1 se rapproche de x² et la racine carrée de x² est égale à x. Ainsi, nous obtenons x/x, ce qui est environ égal à 1 lorsque x tend vers l'infini. Par symétrie, nous pouvons en déduire que lorsque x tend vers moins l'infini, la limite de la fonction sera -1.
Pour la limite en 1 par la droite, nous pouvons voir que lorsque x est légèrement supérieur à 1, x²-1 est toujours positif, ce qui signifie que nous pouvons définir la racine carrée. Cela nous donne 1/0+, ce qui est autorisé. Par symétrie, cela signifie que lorsque x tend vers moins 1 par la gauche, la limite de la fonction est également autorisée et égale à -1.
Maintenant, passons à la limite en moins l'infini. Ici, nous devons faire attention à la racine de x², car lorsque x est négatif, la racine de x² devient la valeur absolue de x. Donc, lorsque x tend vers moins l'infini, nous obtenons la valeur absolue de x, qui est légèrement supérieure à 1. Ainsi, nous pouvons dire que lorsque x tend vers moins l'infini, la racine carrée de x²-1 tend vers 0+.
En utilisant ces limites, nous pouvons conclure que la fonction a une asymptote horizontale en y = 1 pour les limites en plus l'infini, une asymptote verticale en y = -1 pour les limites en 1 par la droite, une asymptote verticale en y = -1 pour les limites en 1 par la gauche, et une asymptote verticale en y = -∞ pour les limites en moins l'infini.
Révisions Maths lycée
Analyse Terminale
MPSI/PCSI

Asymptote oblique
Lors de ce cours sur les asymptotes obliques, l'élève mentionne qu'il a vu ce sujet en première année et qu'il était hors programme à l'époque. Cependant, il explique que les asymptotes obliques sont souvent utilisées et qu'il est important de les maîtriser. Il effectue ensuite des calculs pour simplifier une fonction et déterminer une asymptote oblique. Il explique également comment étudier les variations de la fonction et calcule les limites aux extrêmes de l'intervalle. Enfin, il aborde la question des asymptotes verticales et horizontales, ainsi que la position relative de deux fonctions.
Révisions Maths lycée
Analyse Terminale
MPSI/PCSI
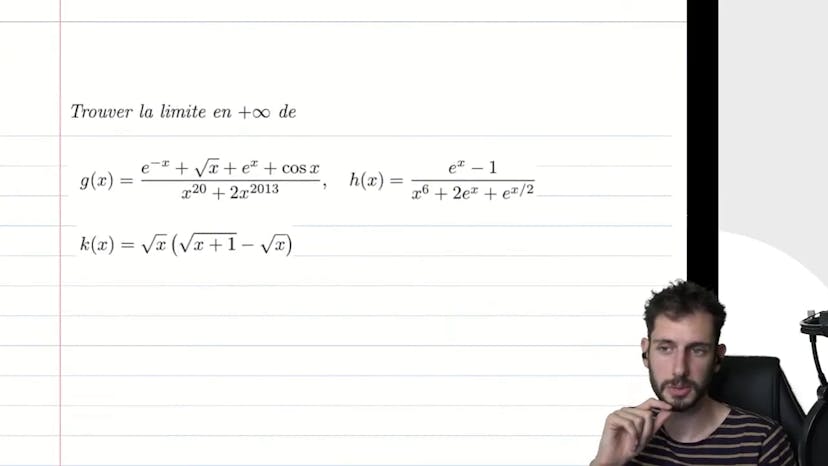
Croissance comparée plus lourde
Ce cours porte sur la croissance comparée en utilisant la fonction exponentielle. L'auteur explique notamment comment comparer la fonction exponentielle avec une autre puissance en utilisant le facteur le plus important, qui est E de x. En simplifiant cette expression, on obtient 1-E de x. Il est facile de gérer cette expression car E de x tend vers 0 lorsque x tend vers l'infini. De plus, l'exponentielle de moins x tend également vers 0 lorsque x tend vers l'infini. En utilisant ces concepts, on peut déduire que E de x sur x puissance 6 tend vers l'infini lorsque x tend vers l'infini. Cependant, il faut noter que cette tendance est inverse pour x6 sur E de x. En résumé, il est important de savoir que ces expressions tendent vers 0 lorsque x tend vers l'infini.
Révisions Maths lycée
Analyse Terminale
MPSI/PCSI
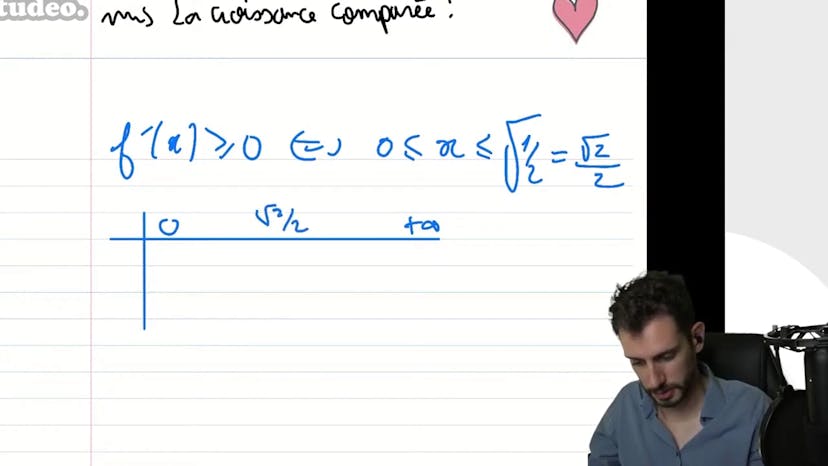
Difficile : BAC 2009
Ce cours porte sur une étude de fonction, plus précisément sur une fonction exponentielle. Le professeur explique comment trouver la limite de la fonction lorsque x tend vers l'infini et montre comment utiliser la croissance comparée pour résoudre ce problème. Ensuite, il procède à une analyse de la dérivabilité de la fonction et montre comment calculer la dérivée. En utilisant les propriétés de la dérivée, il détermine les intervalles où la fonction est positive ou nulle. Enfin, il construit un tableau de variations de la fonction et détermine le maximum de la fonction en une valeur spécifique de x. Il donne également la valeur de la fonction à cet endroit.
Révisions Maths lycée
Analyse Terminale
MPSI/PCSI

Exp : indéterminée en -∞
Le cours porte sur la démonstration d'une formule mathématique. L'exercice consiste à appliquer les règles des puissances pour simplifier l'expression. Ensuite, en utilisant certaines formules mathématiques connues, on peut conclure que la courbe a une asymptote horizontale à y=1. Enfin, on étudie les variations de la dérivée de la fonction et on montre qu'elle est positive ou nulle pour certains intervalles de x. On conclut en donnant les limites et asymptotes de la fonction.
Révisions Maths lycée
Analyse Terminale
MPSI/PCSI

Vers la SUP : Quantité conjuguée
L'exercice en question concerne le calcul d'une somme avec une limite infinie. Il est important de comprendre que c'est la variable x qui tend vers l'infini, pas le nombre d'éléments n de la somme. Pour faciliter le calcul, on peut utiliser la méthode de la quantité conjuguée, qui consiste à prendre une différence de racines. Dans ce cas, les n termes de la somme peuvent être compensés par des racines supplémentaires. En réorganisant les termes, on obtient une identité remarquable qui facilite le calcul. Finalement, en remarquant que tous les termes tendent vers zéro, on peut conclure que la somme tend vers zéro lorsque x tend vers l'infini. Il est important de ne pas se laisser distraire par des erreurs courantes, comme confondre le n avec le x, et de prendre le temps d'analyser calmement les différentes méthodes à appliquer.
Révisions Maths lycée
Analyse Terminale
MPSI/PCSI
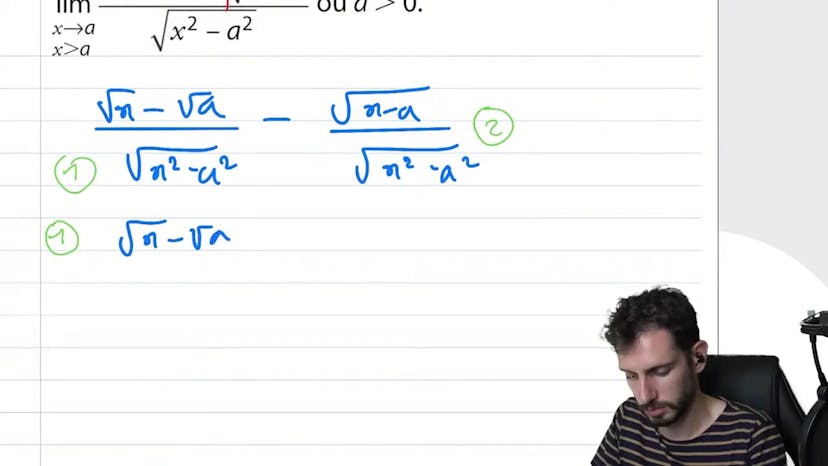
Quantité conjugée piégeuse
Le cours aborde la notion de quantité conjuguée dans le domaine des mathématiques. L'orateur explique qu'il est important de ne pas confondre une quantité conjuguée avec une simple addition ou une différence de racines. Il propose ensuite une méthode pour traiter une certaine équation en séparant la fraction en deux parties distinctes. Il utilise ensuite la quantité conjuguée pour simplifier le calcul et parvient à obtenir une expression plus simple. Il conclut en donnant le nom de la fonction étudiée et son comportement lorsque x tend vers a.


