Online Electrocinétique course by Top Instructors - Electrocinétique

Association de dipôles

Dans cette vidéo, Mathilde Studio explique comment associer des dipôles de manière complexe. Elle commence par montrer un bout de circuit composé d'une résistance et d'un condensateur en série. Elle explique ensuite comment déterminer l'impédance équivalente aux dipôles en régime sinusoidal, ainsi que sa résistance et sa réactance. Elle souligne que l'impédance équivalente permet d'identifier des dipôles à des résistances, tout comme les associations de résistances. Elle montre comment l'impédance des dipôles en série s'ajoutent pour donner la somme des impédances. Elle déduit la nature des dipôles ainsi formés, qui comportent une partie résistive et une partie capacitive. Elle explique comment relier la tension complexe E qui s'applique à l'ensemble des dipôles au courant complexe I qui les traverse, et comment obtenir des signaux en quadrature de phase. Elle détermine finalement l'expression réelle de E pour I², qui vaut I0 sin ωt, en appliquant la loi d'Ohm en complexe et en utilisant une manipulation qui consiste à passer du signal complexe au signal réel en intégrant ou en dérivant. Elle insiste sur l'importance de cette transformation en complexe pour simplifier les calculs.

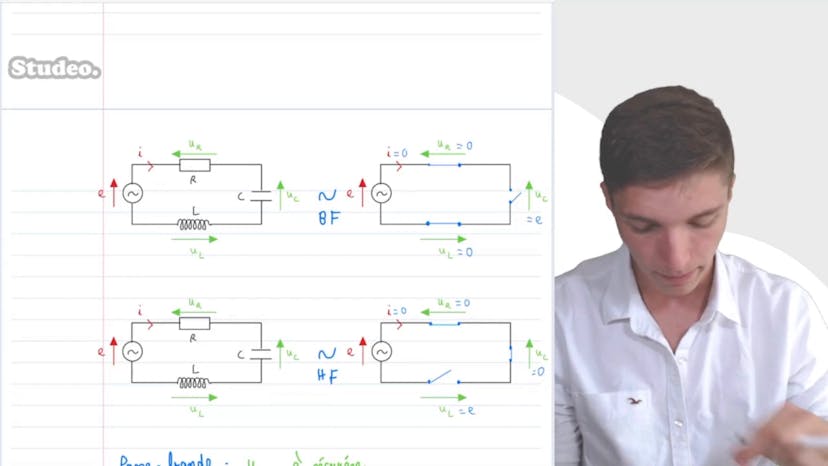
Créer un filtre

Dans cette vidéo, Matisse de Studio explique comment créer un filtre à partir d'un circuit RLC série. Pour choisir la tension de sortie et réaliser un filtre passe-vente, il faut analyser le comportement asymptotique du filtre en basses et hautes fréquences. Les impédances complexes des dipôles (bobine et condensateur) déterminent si l'interrupteur est ouvert ou fermé et si la tension est récupérée aux bandes de résistance, aux bandes du condensateur ou aux bandes de la bobine. Les filtres peuvent être utilisés dans différents domaines industriels, tels que l'imagerie ou l'étude sonore, pour réaliser des filtres passe-bandes, passe-haut et passe-bas.

Filtre passe-haut RLC

Bonjour à tous, dans cette vidéo, nous allons réaliser un filtre passe-eau pour un circuit RLC série. Pour cela, nous devons justifier que ce filtre est bien passe-eau, définir sa pulsation caractéristique ω0 et son facteur de qualité Q. Pour déterminer le caractère passe-eau du circuit, nous devons mener une étude asymptotique. Dans une précédente vidéo, nous avons démontré que le circuit RLC série est équivalent à un circuit basse fréquence et un circuit haute fréquence. Ainsi, pour réaliser un filtre passe-eau, nous devons sélectionner la tension aux bornes de la bobine, car elle filtre les basses fréquences. La pulsation propre et le facteur de qualité du filtre peuvent être déterminés en utilisant la méthode classique pour un circuit RLC série. Nous devons ensuite exprimer la fonction de transfert du filtre sous la forme h = jqx / (1 + jqx - 1/x). Pour cela, nous utilisons le diviseur de tension avec les impédances complexes. En normalisant la fonction de transfert, nous obtenons l'équation demandée. Ensuite, nous devons déterminer les pentes des asymptotes du diagramme de Bode-Anguin, en supposant que le facteur de qualité du circuit n'est pas raisonnable. Pour calculer le module de la fonction de transfert, nous utilisons l'expression qx / (1 + q²x² - 1/x²) et déterminons le terme dominant en basse fréquence et en haute fréquence. En basse fréquence, la pente est de 40 décibels par décade et en haute fréquence, la pente est de 0. En traçant le diagramme de Bode en fonction du logarithme de la pulsation, nous pouvons esquisser l'allure du filtre passe-eau. Enfin, nous étudions si le filtre peut avoir un comportement dérivateur ou intégrateur. Cela se remarque sur le diagramme de Bode par une pente de plus ou moins 20 décibels par décade. Dans ce cas, le filtre n'a pas de comportement dérivateur ou intégrateur. Le diagramme de Bode est donc un outil très utile pour visualiser rapidement les caractéristiques d'un filtre. Merci pour cette étude du filtre passe-eau d'un RLC et à bientôt.

Filtre RL série

Dans cette vidéo, on étudie un filtre RL série qui permet de réaliser un filtre passe-bas du premier ordre. En effet, la bobine a une impédance complexe qui tend vers zéro en basse fréquence et qui s'oppose au courant en haute fréquence, ce qui coupe les basses fréquences. La fonction de transfert du filtre est H = H0Jω/ωc / (1+Jω/ωc), où ωc est la pulsation de coupure du filtre. Les pentes des asymptotes en gain dans les limites hautes et basses fréquences sont respectivement de plus 20 dB par décade et de 0, ce qui caractérise un circuit du premier ordre avec une différence de 20 dB entre les deux asymptotes. Les filtres du second ordre ont une différence de 40 dB entre les deux asymptotes. Enfin, la méthode de vérification supplémentaire permet de confirmer que ce circuit est du premier ordre.

Signal non harmonique

Dans cette vidéo, on apprend à filtrer un signal non harmonique en utilisant la transformation de Fourier et une fonction de transfert harmonique. Le signal d'entrée est une forme d'onde créneau et sa représentation temporelle est donnée en série de Fourier. Le filtre utilisé est un filtre passe-bas dont la fonction de transfert est donnée en jω. En utilisant l'analyse complexe et la formule de filtrage linéaire, on détermine l'expression du signal de sortie en fonction de la fonction de transfert et du signal d'entrée. Il est important de comprendre cette résolution pour maîtriser l'enjeu du filtrage linéaire en électricité.

Circuit bouchon

Dans cette vidéo, nous étudions le circuit Bouchon, qui est constitué d'un dipôle avec une bobine et un condensateur montés en dérivation. Nous déterminons l'impédance complexe ZS d'un dipôle RLC série en fonction des composants, de R, de la pulsation propre et du facteur de qualité. Ensuite, nous exprimons l'impédance complexe Z du dipôle parallèle sous la forme R divisé par JCωZS, facteur de 1 plus JQω sur ω0. Nous montrons que lorsque le facteur de qualité est très élevé et la pulsation pas trop faible, l'impédance peut se mettre sous la forme approchée Z est environ égal à Q²R² sur ZS complexe. Nous déterminons également que le module de l'impédance complexe est maximal lorsque la pulsation est égale à la pulsation propre ω0, et que le circuit est alors bloqué, d'où l'appellation circuit bouchon. Enfin, nous déterminons les intensités réelles qui traversent respectivement le condensateur et la bobine en fonction de E0, Q et R, et constatons que le circuit est véritablement un circuit bouchon.

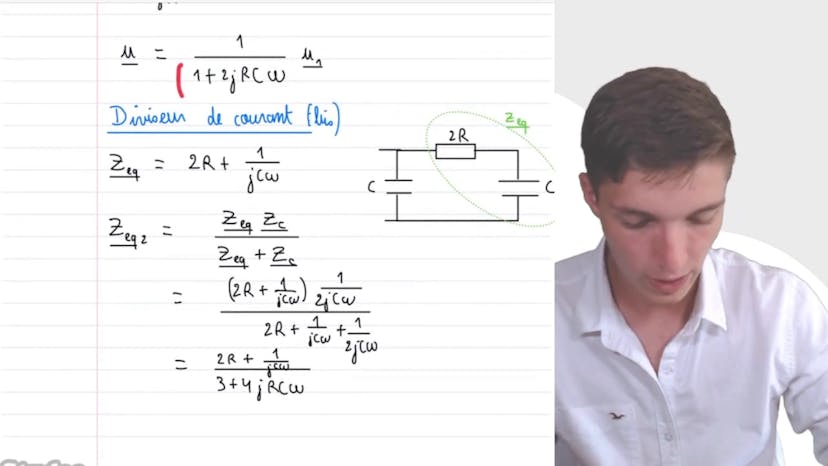
Equation différentielle via les complexes

Dans cette vidéo, Matisse de Studio explique comment établir une équation différentielle en utilisant les complexes. L'équation à déterminer est 4 tau² d2u sur dt2 plus 5 tau du sur dt plus U est égal à E. À l'aide d'un diviseur de tension, la tension U peut être exprimée en fonction d'une tension intermédiaire U1, qui peut ensuite être exprimée en fonction de la tension de départ E. En utilisant des manipulations de grandeurs complexes, Matisse détermine l'impédance équivalente et applique le diviseur de tension pour obtenir la relation entre U et E en complexe. En repassant ensuite en réel, l'équation différentielle est obtenue. Cette méthode démontre la puissance de la résolution à l'aide des complexes pour obtenir des résultats électro-signétiques de manière plus simple.

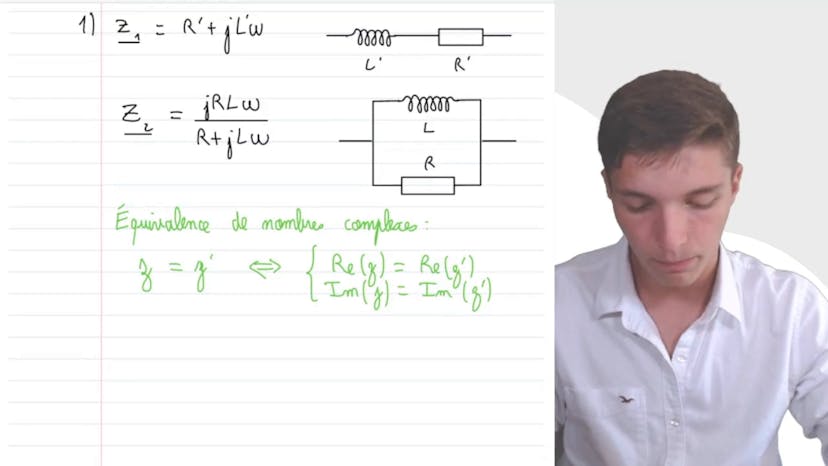
Equivalence entre deux dipôles

Dans cette vidéo, nous étudions l'équivalence entre deux dipôles complexes en régime sinusoidal forcé de pulsation oméga. Les dipôles sont constitués d'une bobine d'inductance L et d'une résistance R en série ou en parallèle. Pour être équivalents, les deux dipôles doivent avoir les mêmes impédances complexes. Pour cela, nous déterminons leurs impédances complexes en fonction de oméga. Ensuite, nous extrayons leurs parties réelles et imaginaires pour les comparer. Si nous remplaçons la bobine L par un condensateur C, nous obtenons une relation qui est impossible à satisfaire car la capacité serait strictement négative. En conclusion, nous travaillons avec des nombres complexes comme les autres pour déterminer l'équivalence des dipôles.

Filtre de Wien

Dans cette vidéo, Matisse de Studio nous parle du filtre de Wien. Il explique que ce filtre est utilisé dans les oscillateurs autant entretenus et qu'il est assez simple à réaliser. En analysant les comportements asymptotiques, il détermine que c'est un filtre passe-bas. Ensuite, il calcule la fonction de transfert du filtre en utilisant le diviseur de tension. Il obtient une expression satisfaisante en normalisant la fonction de transfert. Il introduit également les notions de ω0 et de X. Il écrit ensuite la fonction de transfert sous une forme canonique, avec H égal à H0 divisé par 1 plus JQ, où H0 est 1/3 et Q est 1/3. Matisse calcule ensuite le gain maximal du filtre, qui est égal à H0, soit 1/3. Il exprime également sa valeur en décibels, qui est d'environ -9,5 décibels. Il calcule également le déphasage correspondant, qui est de 0. En représentant le diagramme de Bode, il montre que le gain en décibels a une pente de +20 en 0 et -20 en infini, avec un maximum à la fréquence ω0. La phase varie de π/2 à -π/2. Ensuite, Matisse explique comment calculer la pulsation propre ω0 pour certaines valeurs et donne le signal de sortie du filtre si le signal d'entrée est E0+ E0cos(ωt) + E0cos(10ωt) + E0cos(100ωt). Il utilise la méthode de filtrage linéaire pour calculer le signal de sortie en appliquant la fonction de transfert aux différentes composantes du signal d'entrée. Il montre que la composante continue est coupée par le filtre, que la composante à ω0/10 a un gain de 1/10 et une phase de -1.2 radian, et que la composante à ω0 a un gain de 1/3 et pas de phase supplémentaire. Il montre également que la composante à 10ω0 a un gain de 1/10 et une phase de 1.2 radian. Finalement, il donne le signal de sortie, qui est la somme de toutes les composantes filtrées. En conclusion, le filtre de Wien est un filtre passe-bas utilisé dans les oscillateurs autant entretenus. Sa fonction de transfert est H = H0/(1 + JQ(X - 1/X)), avec H0 = 1/3 et Q = 1/3. Son gain maximal est de 1/3, ce qui correspond à environ -9,5 décibels, et son déphasage est de 0. Il permet de filtrer les différentes composantes d'un signal d'entrée pour obtenir un signal de sortie filtré.

Mesures à l'ampèremètre

Dans cette vidéo, on étudie des mesures effectuées à l'en-permettre. Il s'agit d'un circuit avec 6 comptes, alimenté par une tension sinusoidale UAB et avec une pulsation particulière oméga qui permet d'obtenir la même valeur de l'em-permettre en mode AC dans trois situations différentes. Ces situations impliquent des courants différents traversant différents dipôles du circuit. Pour déterminer la valeur de cette pulsation oméga, il faut établir une condition sur les valeurs des composants du circuit (L, C et R). En exprimant les lois d'Ohm en complexe, on obtient trois expressions pour les courants et on peut les ramener à des grandeurs communes en exploitant la loi d'Ohm. On mesure l'intensité du courant efficace avec l'ampèremètre, qui correspond à la valeur maximale divisée par la racine de 2, et le module des impédances des dipôles est déterminant pour obtenir des valeurs efficaces identiques pour les trois courants. En imposant cette condition sur les modules des impédances et en calculant le carré de ces modules, on obtient une condition sur les valeurs de L, C et R qui permet de déterminer la valeur de la pulsation oméga. En isolant R dans une expression qui contient et qui ne contient pas cette valeur, on peut également obtenir une condition sur la valeur de R. En manipulant les complexes, on apprend à exprimer les grandeurs complexes associées aux instruments expérimentaux.