Online Arithmétique dans Z course by Top Instructors - Arithmétique dans Z

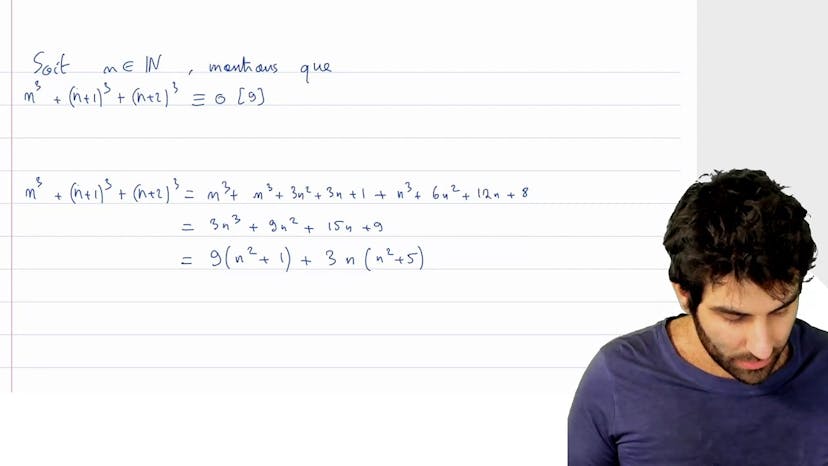
Cubes consécutifs

Dans cet exercice, on démontre que la somme de 3 cubes consécutifs est toujours divisible par 9. Pour cela, on utilise les congruences pour simplifier les résultats. On veut montrer que la somme de 3 cubes consécutifs, soit n^3 + (n+1)^3 + (n+2)^3, est congru à 0 modulo 9. En développant cette expression, on obtient 3n^3 + 9n^2 + 15n + 9. On regroupe les termes pour faciliter les calculs et remarquons que le premier terme est déjà divisible par 9. En factorisant le deuxième terme par 3n et le troisième terme par 3, on obtient 9(n^2 + 1)(3n + 5). Il est facile de voir que le terme 9(n^2 +1) est congru à 0 modulo 9 car il est divisible par 9. De plus, le terme 3n + 5 est congru à 0 modulo 3 car il est divisible par 3. Ainsi, nous avons démontré que pour tout n, la somme de 3 cubes consécutifs est divisible par 9.

Congruences avec les puissances

Dans cet exercice, l'objectif est de trouver le reste de la division par 13 du nombre 100 puissance 1000. Pour cela, il est recommandé d'utiliser les congruences plutôt qu'une calculatrice en raison de la taille du nombre. Tout d'abord, on détermine le reste de la division de 100 par 13, qui est 9. Ensuite, au lieu de travailler avec 100, on travaillera avec 9 car ils sont congruents modulo 13. Par exemple, si 100 puissance 4 est congru à 1 modulo 13, alors 9 puissance 4 sera aussi congru à 1 modulo 13. On calcule donc les puissances de 9. On constate que 9 puissance 2 est congru à 3 modulo 13, mais ce n'est pas ce que l'on souhaite. On cherche à trouver une puissance de 9 qui est congru à 1 modulo 13, et on trouve que 9 puissance 3 est congru à 1 modulo 13. Donc la puissance recherchée est 3. On réécrit alors 100 puissance 3 comme congru à 9 puissance 3, qui est congru à 1 modulo 13. Etant donné que 100 puissance 3 est congru à 1 modulo 13, le nouveau diviseur sera 3 cette fois-ci. On effectue donc une division euclidienne de 1000 par 3, ce qui donne 333 avec un reste de 1. On réécrit alors 100 puissance 1000 comme 100 puissance 3 fois 333 plus 1, en utilisant les règles de calcul sur les puissances. Cela devient donc (100 puissance 3) puissance 333 multiplié par 100. Il est important de ne pas se tromper en interprétant cela comme (100 puissance 333) puissance 3, car cela engendrerait une interprétation différente. Ici, on écrit cette expression de cette façon spécifique car on sait que 100 puissance 3 est congru à 1 modulo 13, et que 100 est congru à 9. Ainsi, on peut remplacer 100 par 9 dans l'expression. En considérant que 1 puissance 333 est égal à 1 modulo 13, le calcul final donne que 1 puissance 333 fois 9 est congru à 9 modulo 13. Par conséquent, selon la définition des congruences, le reste de la division euclidienne de 100 puissance 1000 par 13 est égal à 9.

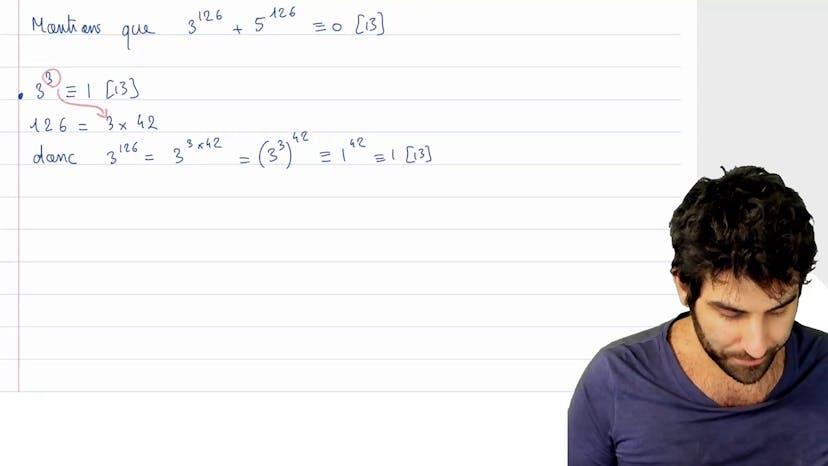
Division de puissances

Dans cet exercice, nous allons montrer que 13 divise 3^126 + 5^126 en utilisant les congruences. Au lieu de montrer que chaque terme est congru à 0 modulo 13, nous allons examiner à quoi chaque terme est congru modulo 13. Pour cela, nous cherchons d'abord une puissance de 3 qui est congrue à 1 modulo 13. Nous trouvons que 3^3 ≡ 1 modulo 13. Ensuite, nous divisons 126 par 3 pour obtenir 42 sans reste. Ainsi, 3^126 = (3^3)^42 ≡ 1^42 ≡ 1 modulo 13. De la même manière, nous cherchons une puissance de 5 qui convient. Nous trouvons que 5^3 ≡ 8 modulo 13. Ensuite, nous divisons 126 par 4 pour obtenir 31 avec un reste de 2. Ainsi, 5^126 = (5^4)^31 * 5^2 ≡ 1^31 * 12 ≡ 12 modulo 13. Finalement, nous avons montré que 3^126 ≡ 1 modulo 13 et 5^126 ≡ 12 modulo 13. Donc, 3^126 + 5^126 ≡ 1 + 12 ≡ 0 modulo 13. Ainsi, nous concluons que 13 divise bien 3^126 + 5^126.

Equation type Fermat

Dans cet exercice, on doit résoudre une équation avec des coefficients entiers. On nous demande de montrer que si n, a et b sont des entiers tels que n est un multiple de 4 et que l'équation n = a² + b² est vérifiée, alors a et b doivent être pairs. Pour prouver cela, on va utiliser une preuve par l'absurde. On suppose d'abord que a et b sont impairs. On peut alors écrire a comme 2k + 1 et b comme 2k' + 1, où k et k' sont des entiers. On développe ensuite l'équation a² + b² et on factorise par 4. On remarque que cela nous donne 4 fois un nombre entier plus 2. Cependant, cela implique que a² + b² est congru à 2 modulo 4, ce qui contredit le fait que n est un multiple de 4. Donc, l'hypothèse selon laquelle a et b sont impairs est fausse. Ensuite, on suppose qu'un des deux nombres a ou b est impair. Nous pouvons supposer sans perte de généralité que c'est a qui est impair et que b est pair. En utilisant le même raisonnement, on arrive à la conclusion que a et b doivent tous les deux être pairs pour que n soit un multiple de 4. En utilisant cette conclusion, on peut également montrer que l'équation 2^(2n) = a² + b² n'a pas de solution. En supposant qu'il existe une solution et en notant n0 le plus petit entier tel que 2^(2n0) = a² + b², on montre de manière contradictoire que cette équation n'a pas de solution en utilisant la minimalité de n0. Enfin, on nous demande de démontrer que l'équation 2^(2n) + 1 = a² + b² a une unique solution. On montre d'abord qu'une solution est donnée par a = b = 2^n en décomposant 2^(2n) + 1 en 2 (2^n)^2. Ensuite, on utilise une preuve par récurrence pour montrer que c'est la seule solution. On suppose que cela est vrai pour un certain rang n et on montre que cela est aussi vrai pour n+1, en utilisant le fait que 2^(2n+3) est un multiple de 4 et en appliquant notre hypothèse de récurrence. Ainsi, on peut conclure que l'équation 2^(2n) + 1 = a² + b² admet une unique solution donnée par a = b = 2^n.

Divisbilté par 7

Dans cet exercice, il s'agit de démontrer que pour tout nombre naturel n, l'expression 3 puissance 2n plus 1 plus 2 puissance 4n plus 2 est divisible par 7. Pour cela, on utilise une méthode de récurrence. On commence par le cas initial, n=0. En substituant n par 0 dans l'expression, on obtient 3 puissance 1 plus 2 puissance 2, qui est égal à 7. Donc, dans ce cas, 7 divise bien l'expression. Ensuite, on passe au cas de n à n+1. On veut montrer que l'expression 3 puissance 2n plus 3 plus 2 puissance 4n plus 6 est congruente à 0 modulo 7. Pour cela, on utilise les congruences. On factorise l'expression en extrayant 3 puissance 2 et 2 puissance 4 (car un 2 et un 4 sont sortis lors du passage de n à n+1). En utilisant les propriétés des congruences modulo 7, on peut simplifier l'expression et la réécrire comme 2 * (3 puissance 2n plus 1 plus 2 puissance 4n plus 2). Or, on reconnaît que cette expression est congruente à 0 modulo 7, grâce à l'hypothèse de récurrence. En effet, on sait que pour tout n antinaturel, l'expression 3 puissance 2n plus 1 plus 2 puissance 4n plus 2 est divisible par 7. Donc, si cette expression est congruente à 0 modulo 7, l'expression 3 puissance 2n plus 3 plus 2 puissance 4n plus 6 l'est également. Finalement, on a bien démontré que pour tout n, l'expression 3 puissance 2n plus 1 plus 2 puissance 4n plus 2 est divisible par 7.