 All subjects
All subjects
 All subjects
All subjects
Révisions Maths lycée
Analyse Terminale
MPSI/PCSI

Dérivabilité et Variations
Le cours porte sur l'étude d'une fonction logarithmique. La fonction donnée est ln(2x)/(ln(2x)-1). Elle est définie pour x appartenant à (0, +∞), à l'exception de x = e. Pour étudier cette fonction, on applique la méthode classique de dérivation. La dérivée de la fonction est g'(x) = -2x/(ln(2x)-1)². On observe que g'(x) est strictement négatif sur son domaine de définition. Par contre, il y a une valeur interdite en x = e, où le dénominateur s'annule. Par conséquent, la fonction est décroissante sur (0, e) et sur (e, +∞), mais il y a un décrochage à x = e. Lorsqu'il y a une valeur interdite, il est courant d'avoir une division par zéro, où la fonction diverge vers l'infini positif d'un côté et vers l'infini négatif de l'autre. Ainsi, le tableau de variations complet est obtenu en analysant les limites de g en 0, e-, e+, et +∞. On remarque qu'en 0, g(x) tend vers 1. En e-, g(x) tend vers -∞, tandis qu'en e+, g(x) tend vers +∞. Finalement, en +∞, g(x) tend également vers 1. Le graphe de la fonction présente une asymptote verticale en x = e et une asymptote horizontale en y = 1. La courbe est décroissante jusqu'à x = e, puis remonte vers l'infini. Il est essentiel de noter qu'il y a un saut de -∞ à +∞ à l'asymptote verticale.
Révisions Maths lycée
Analyse Terminale
MPSI/PCSI

Croissance Comparée
Dans ce cours, nous étudions la fonction f(x) = 3-x + 2ln(2x). Nous commençons par dériver cette fonction pour trouver son signe. La dérivée f'(x) = -1 + 2x nous permet de déterminer que la fonction est positive pour x > 1 et négative pour x < 1. Pour x > 0, la dérivée est également positive jusqu'à x = 2, ensuite elle devient négative. Ainsi, nous pouvons conclure que f(x) est croissante sur l'intervalle (0, 2) et décroissante sur l'intervalle (2, +∞).
Ensuite, nous calculons également f(2) pour avoir une vue d'ensemble de la variation de f. Nous obtenons f(2) = 1 + 2ln(2). Pour étudier plus en détail la variation de f, nous analysons les limites de la fonction. Lorsque x tend vers +∞, nous factorisons par le terme prédominant - x, ce qui nous permet de simplifier l'expression et de conclure que la limite est égale à 0. De même, lorsque x tend vers 0, nous arrivons à la conclusion que la limite est également égale à 0. Ainsi, le tableau de variation complet de f est établi.
Enfin, nous étudions la convexité de f en calculant la dérivée seconde f''(x) = -1/x^2. En résolvant cette équation, nous trouvons que f''(x) = 0 pour x ≠ 0. Cela signifie que f est concave sur l'ensemble de son domaine de définition, c'est-à-dire R étoile plus.
En résumé, la fonction f(x) = 3-x + 2ln(2x) est croissante sur (0,2) et décroissante sur (2, +∞). Elle a un maximum en 2 et est concave sur R étoile plus tout entier.
Révisions Maths lycée
Analyse Terminale
MPSI/PCSI

Ln : Limites
Dans ce cours, nous nous intéressons aux calculs de limites faisant intervenir la fonction ln (logarithme népérien). Le principe est de factoriser par le terme prédominant pour simplifier les limites. Pour les limites avec ln, nous essayons de les ramener à des limites usuelles sur le logarithme.
Voici trois exemples :
1. Limite de 2ln2x²-5ln2x±1 : En factorisant par ln2x², nous obtenons une limite qui tend vers l'infini.
2. Limite de ln(racine de x) / ln(2x) : En utilisant les propriétés du logarithme, nous transformons la limite en xlnx/ln2 + lnx. Après une factorisation par ln x, nous obtenons une limite de 1.5.
3. Limite de (x-1)²ln(x-1) : En posant grand x = x-1, nous ramenons la limite à une limite usuelle de x²lnx. Puisque cette limite tend vers 0, nous obtenons que la limite recherchée est égale à 0.
Ces exemples illustrent comment calculer des limites avec le logarithme.
Révisions Maths lycée
Analyse Terminale
MPSI/PCSI

Dériver ln(u)
Le cours traite de la définition du logarithme et de la façon de déterminer l'ensemble de définition d'une fonction contenant un logarithme. Ensuite, il explique comment calculer la dérivée de cette fonction. Le cours donne plusieurs exemples pour illustrer ces concepts. Pour la première fonction, f(x) = ln(8x-4), l'ensemble de définition et de dérivabilité est [1.5, +∞[. La dérivée de cette fonction est f'(x) = 2/(2x-1). Pour la deuxième fonction, f(x) = ln(x² + x + 1), l'ensemble de définition et de dérivabilité est ℝ. La dérivée de cette fonction est f'(x) = 2x/(x² + x + 1). Pour la troisième fonction, f(x) = ln(x-1) - ln(2x+4), l'ensemble de définition et de dérivabilité est ]-∞, -2[ ∪ ]1, +∞[. La dérivée de cette fonction est f'(x) = (6)/(2(x-1)(2x+4)). Pour la dernière fonction, f(x) = ln(e^x), l'ensemble de définition et de dérivabilité est ]0, +∞[. La dérivée de cette fonction est f'(x) = 1. En résumé, il est important de toujours prendre en compte l'ensemble de définition d'une expression contenant un logarithme et de calculer la dérivée de manière appropriée.
Révisions Maths lycée
Analyse Terminale
MPSI/PCSI
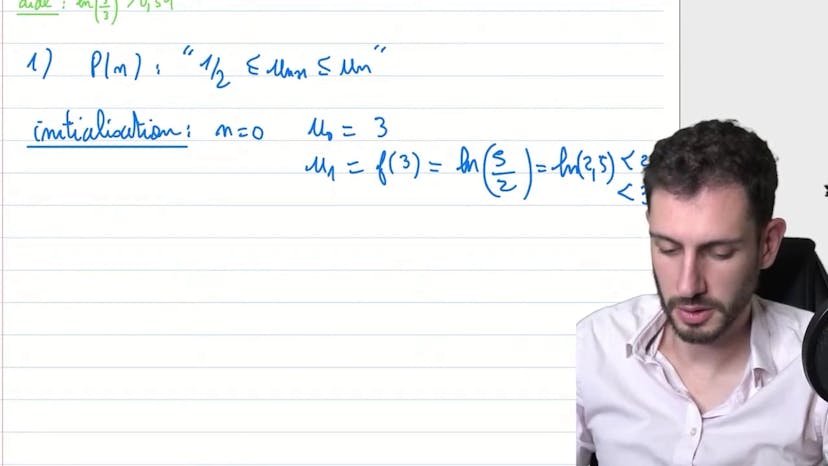
Fonction et suite récurrente associée
Dans ce cours, nous étudions une fonction définie de manière rationnelle, c'est-à-dire avec un degré 1 au-dessus et un degré 1 en dessous de la fraction. La fonction est définie sur l'intervalle de 0 à l'infini. Nous déterminons la limite de cette fonction lorsque x tend vers l'infini en utilisant la composition de fonctions. La limite est égale au logarithme de 3. En utilisant la continuité du logarithme, nous concluons que la fonction est bien définie. Ensuite, nous démontrons que la dérivée de la fonction est égale à 3x+3 pour tout nombre réel positif ou nul. Nous concluons que la fonction est strictement croissante et positive. Ensuite, nous passons à l'étude d'une suite définie par récurrence à l'aide de cette fonction. Nous démontrons par récurrence que la suite est décroissante et minorée par un demi. En utilisant le théorème de convergence des suites décroissantes et minorées, nous concluons que la suite converge vers une limite strictement positive. En résumé, ce cours traite de la définition d'une fonction rationnelle, de la détermination de sa limite, de la démonstration de la dérivée de la fonction, de l'étude d'une suite définie par récurrence à l'aide de cette fonction et de la convergence de cette suite.
Révisions Maths lycée
Analyse Terminale
MPSI/PCSI

Un classique de BAC : étude de fonction en 2 temps
L'exercice consiste à étudier deux fonctions, G(x) et F(x), en calculant leurs limites aux bornes de leur ensemble de définition et en dressant un tableau de variation.
Pour étudier G(x), on remarque que la dérivée de F(x) est similaire à la fonction G(x) donnée. On calcule donc la dérivée de F(x) et on l'étudie. On remarque que la dérivée de F(x) est toujours négative sur R+*, tandis que G(x) est positive avant un certain point et devient négative après ce point.
En calculant les limites de G(x) aux bornes de son ensemble de définition, on trouve que G(x) tend vers 1 en 0+ et tend vers moins l'infini en +infini.
En ce qui concerne F(x), on calcule les limites aux bornes de son ensemble de définition et on trouve que F(x) tend vers moins l'infini en 0 et tend vers 0 en +infini.
En analysant la dérivée de F(x), on remarque que F'(x) a le même signe que G(x), ce qui nous permet de déterminer les variations de F(x) dans le tableau de variation.
On complète le tableau en indiquant que la limite de F(x) est moins l'infini en moins l'infini et 0 en 0+. De plus, on détermine qu'il existe une unique solution à l'équation F(x) = 0.
En résumé, cet exercice consiste à analyser les fonctions G(x) et F(x), à calculer leurs limites aux bornes de leur ensemble de définition et à dresser un tableau de variation pour chacune des fonctions.
Révisions Maths lycée
Analyse Terminale
BCPST

Dérivabilité et Variations
Le cours porte sur l'étude d'une fonction utilisant le logarithme. La fonction en question est ln(2x+1) / ln(2x-1) et est définie sur l'intervalle (0, e) exclu union avec (e, +∞). La dérivée de la fonction est calculée et simplifiée en -2x / (ln(2x-1))^2. La fonction est décroissante sur (0, e) et sur (e, +∞), avec une oscillation entre ces deux intervalles. Il est souligné que les valeurs interdites sont généralement dues à une division par zéro, ce qui peut faire tendre la fonction vers plus ou moins l'infini selon les côtés de la valeur interdite. Les limites de la fonction aux points 0, e- et e+ sont calculées, permettant ainsi la création du tableau de variation complet. Une asymptote verticale d'équation x=e et une asymptote horizontale d'équation y=1 sont observées sur le graphique de la fonction. La décroissance de la fonction est uniquement valable sur les intervalles où elle n'est pas interrompue par les asymptotes. Ce cours présente une méthodologie d'étude de fonction utilisant le logarithme. Pour toute question supplémentaire, il est recommandé de consulter la FAQ.
Révisions Maths lycée
Analyse Terminale
BCPST

Croissance Comparée
Dans cette leçon, nous étudions la fonction f(x) = 3 - x + 2ln(2x). Nous commençons par dériver cette fonction pour trouver son signe. La dérivée est f'(x) = -1 + 2x.
En utilisant le signe de la dérivée, nous pouvons voir que f'(x) est positif pour x ∈ ]0,2[ et négatif pour x ∈ ]2,+∞[. Nous pouvons également calculer f(2) = 1 + 2ln(2).
Ensuite, nous étudions les limites de f(x). En +∞, nous factorisons par x et utilisons la croissance comparée pour trouver que la limite est 0. En 0, nous avons également une limite de 0.
En analysant les variations et les limites, nous construisons le tableau de variation complet de f(x). Nous trouvons que f(x) tend vers -∞ en +∞ et en 0, et qu'il atteint un maximum en x = 2.
Enfin, nous étudions la convexité de f(x) en dérivant une deuxième fois. La dérivée seconde est f''(x) = -1/x^2, qui est strictement négative sur R étoile plus. Par conséquent, f(x) est concave sur R étoile plus.
Voilà, nous avons maintenant étudié les variations et la convexité de la fonction f(x) = 3 - x + 2ln(2x). Si vous avez des questions supplémentaires, n'hésitez pas à consulter notre FAQ.
Révisions Maths lycée
Analyse Terminale
BCPST

Ln : Limites
Dans ce cours, nous nous intéressons aux calculs de limites impliquant la fonction ln. Le principe général consiste à factoriser par le terme dominant pour simplifier le calcul. Lorsque nous avons une expression avec le ln, nous cherchons à la ramener à des limites usuelles. Nous examinons cela cas par cas.
Dans le premier exemple, nous avons l'expression 2ln(2x²) - 5ln(2x) ± 1. En factorisant par ln(2x²), nous obtenons 2, 5/ln(2x), et 1/ln(2x²), qui tendent tous vers 0. Ainsi, la limite de cette expression est +∞.
Dans le deuxième exemple, nous avons ln(√x) / ln(2x) en +∞. Comme il n'y a qu'un seul terme au numérateur et un seul terme au dénominateur, nous utilisons les propriétés du logarithme pour transformer l'expression. Nous savons que ln(A*B) est égal à ln(A) + ln(B), et donc, ln(x^(1.5)) est égal à 1.5*ln(x). Nous factorisons ensuite par 1.5, obtenant x*ln(x) / (ln(2) + ln(x)). En factorisant par ln(x), nous obtenons 1 + ln(2) / ln(x), qui tend vers 0. Finalement, cette fraction tend vers 1.5.
Dans le troisième exemple, nous avons la limite en 1 de (x-1)^2 * ln(x-1). En utilisant la limite usuelle x*ln(x), nous posons g(x) = x-1, afin de transformer l'expression en g(x)^2 * ln(g(x)). Cela revient à x^2 * ln(x), qui est une limite usuelle tendant vers 0. Ainsi, la limite recherchée est égale à 0.
En utilisant les propriétés du logarithme, ln(AB) = ln(A) + ln(B) et ln(A^n) = n*ln(A), nous pouvons simplifier ces calculs de limites faisant intervenir le ln. Si vous avez des questions supplémentaires, consultez la FAQ.
Révisions Maths lycée
Analyse Terminale
BCPST

Dériver ln(u)
Dans ce cours, nous apprenons qu'il est important de faire attention lorsque nous utilisons le logarithme, car il n'est défini que sur Réactoire+. Lorsque nous travaillons avec une expression qui comprend le logarithme, il est essentiel de regarder attentivement son ensemble de définition. Nous nous concentrons sur la méthode pour déterminer l'ensemble de définition d'une fonction avec le logarithme et calculer sa dérivée.
Pour le premier exemple, nous avons la fonction f(x) = ln(8x-4). La fonction ln est définie et dérivable sur R étoile plus. Nous observons que 8x-4 doit être supérieur à 0, ce qui donne x strictement supérieur à 1,5. Ainsi, l'intervalle de définition et de dérivabilité de la fonction f est [1,5, +∞). En calculant la dérivée de f, qui est u' / u avec u = 8x-4, nous obtenons f'(x) = 2 / (2x-1).
Pour le deuxième exemple, nous avons la fonction f(x) = ln(x² + x + 1). Nous remarquons que le polynôme x² + x + 1 est de degré 2 et strictement positif, car son discriminant est strictement négatif. Ainsi, la fonction f qui est de la forme ln(g) est définie et dérivable sur R, car le polynôme est toujours strictement positif. La dérivée de f est f'(x) = g' / g avec g = x² + x + 1, ce qui donne f'(x) = 2x / (x² + x + 1).
Pour le troisième exemple, nous avons la fonction f(x) = ln(u / v) avec u = x - 1 et v = 2x + 4. Nous devons étudier le signe de cette fonction pour déterminer quand elle est strictement positive. En construisant un tableau de signes pour u - 1 et 2x + 4, nous voyons que f(x) est strictement positive dans l'intervalle (-∞, -2) U (1, +∞). L'intervalle de définition et de dérivabilité de f est donc (-∞, -2) U (1, +∞). Pour calculer la dérivée de f, qui est u'v - u"v / v², nous simplifions l'expression en remplaçant u / v par une seule variable. Après calculs, nous obtenons f'(x) = 6 / (2x² + 8x).
Enfin, dans le dernier exemple, nous avons la fonction f(x) = ln(e^x). Comme d'habitude, nous regardons quand l'expression à l'intérieur du logarithme est strictement positive, c'est-à-dire pour x strictement supérieur à 0. Ainsi, la fonction f est définie et dérivable sur R étoile plus. En calculant la dérivée de f, qui est e^x / e^x = 1, nous obtenons f'(x) = 1.
En résumé, il est crucial de toujours faire attention à l'ensemble de définition lorsque nous utilisons le logarithme. Nous devons également mémoriser certaines formules pour calculer les dérivées des fonctions logarithmiques.
Révisions Maths lycée
Analyse Terminale
BCPST
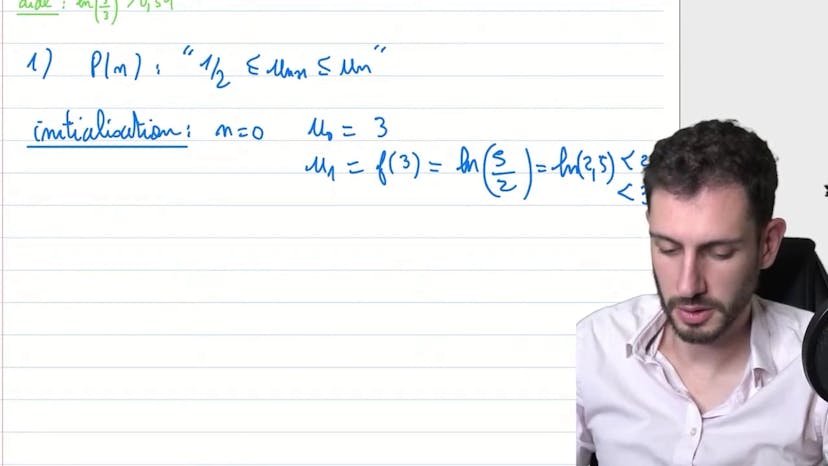
Fonction et suite récurrente associée
Dans ce cours, on étudie une fonction définie par une fraction rationnelle et on détermine sa limite quand x tend vers l'infini. On constate que la fonction a un plateau vers lequel elle tend, avec une limite égale à log(3). Ensuite, on démontre que la dérivée de la fonction est égale à 3x+3. On conclut que la fonction est strictement croissante et on résout un exercice de suite en montrant qu'elle est décroissante et minorée par un demi. Enfin, on rappelle le théorème de convergence des suites croissantes et majorées, et des suites décroissantes et minorées.
Révisions Maths lycée
Analyse Terminale
BCPST

Un classique de BAC : étude de fonction en 2 temps
Ce cours est un exercice classique d'étude de fonctions. On donne deux fonctions, G et F, et on les étudie. Pour étudier G, nous devons calculer sa dérivée et étudier ses limites aux bornes de l'ensemble de définition. En dérivant G, nous obtenons une expression similaire à G elle-même, ce qui nous permet de conclure que G est dérivable sur son ensemble de définition. En calculant les limites de G aux bornes de l'ensemble de définition, nous obtenons les valeurs 1 et moins l'infini. En utilisant ces informations, nous pouvons dresser un tableau de variation de G.
En ce qui concerne F, nous devons également calculer ses limites aux bornes de l'ensemble de définition et dresser un tableau de variation. En calculant les limites de F aux bornes de l'ensemble de définition, nous obtenons les valeurs moins l'infini et 0. En étudiant la dérivée de F, nous remarquons qu'elle correspond à la fonction G. Nous pouvons donc utiliser les informations du tableau de variation de G pour déduire les variations de F. En utilisant ces données, nous dressons un tableau de variation pour F.
En conclusion, nous avons réussi à étudier les fonctions G et F en calculant leurs limites, en étudiant leurs dérivées et en dressant des tableaux de variation.
Révisions Maths lycée
Analyse Terminale
ECG

Dérivabilité et Variations
Nous allons maintenant étudier une fonction qui fait intervenir le logarithme. Nous allons voir comment effectuer une étude de fonction avec les logarithmes. La fonction proposée est ln(2x+1) / ln(2x-1). Elle est définie sur l'intervalle de 0 exclu à l'infini. Nous ne pouvons pas avoir e dans l'intervalle à cause du dénominateur qui s'annulerait. La dérivée de cette fonction est -2x / (ln(2x-1))^2. Cette dérivée est strictement négative sur l'intervalle considéré. Il y a une valeur interdite en e, ce qui signifie que la fonction n'est pas décroissante sur tout l'intervalle. La fonction descend jusqu'à un certain point puis remonte à l'infini. Lorsqu'il y a une valeur interdite, c'est souvent parce qu'il y a une division par zéro, ce qui entraîne une variation de signe de part et d'autre de cette valeur. Nous allons donc étudier les limites de la fonction pour avoir un tableau de variation complet. En 0, la fonction tend vers 1. Pour les valeurs inférieures et supérieures à e, la fonction tend respectivement vers moins l'infini et plus l'infini. Donc notre tableau de variation est complet. Si nous représentons graphiquement la fonction, nous pouvons observer qu'elle possède une asymptote verticale en x = e et une asymptote horizontale en y = 1. La fonction est décroissante jusqu'à un certain point, puis décroît à nouveau. Il est important de noter qu'il y a un saut de moins l'infini à plus l'infini, ce qui signifie que la fonction n'est pas décroissante sur tout l'intervalle considéré. Voilà pour cette méthode d'étude de fonction utilisant les logarithmes. Si vous avez des questions, vous pouvez consulter la FAQ.
Révisions Maths lycée
Analyse Terminale
ECG

Croissance Comparée
Ce cours traite de l'utilisation des croissances comparables pour l'étude des limites avec le logarithme, ainsi que d'une question bonus sur la convexité. La fonction étudiée, f(x) = 3-x + 2ln(2x), est dérivable sur R étoile plus (l'ensemble des réels strictement positifs). La dérivée f'(x) = -1 + 2x, est positive pour x > 0 et inférieur à 2, et négative pour x > 2. La valeur de f(2) est égale à 1 + 2ln(2). Les limites de f(x) lorsque x tend vers plus l'infini et vers 0 sont respectivement moins l'infini et 0. Le tableau de variation complet de f montre un maximum en x = 2. En ce qui concerne la convexité, la dérivée seconde f''(x) = -1/x^2 est strictement négative sur R étoile plus, ce qui signifie que f est concave sur R étoile plus.
Révisions Maths lycée
Analyse Terminale
ECG

Ln : Limites
Dans ce cours, nous nous intéressons aux limites faisant intervenir la fonction ln. Le principe est de factoriser par le terme prédominant pour simplifier les limites. On essaie également de se ramener à des limites usuelles sur le logarithme.
Le premier exemple est 2ln(2x²) - 5ln(2x) ± 1. On factorise par ln(2x²), ce qui donne 2, 5/ln(2x) et 1/ln(2x²) qui tendent tous vers 0. Donc la limite est plus l'infini.
Le deuxième exemple est ln(√x) / ln(2x) en plus l'infini. On ne peut pas factoriser car il n'y a qu'un terme au numérateur et un seul terme au dénominateur. On utilise alors les propriétés du logarithme pour transformer ln(√x) en ln(x^(1/2)), qui devient 1.5ln(x). On factorise par ln(x) et simplifions pour obtenir la limite qui vaut 1.5.
Le troisième exemple est (x-1)²ln(x-1). On pose grand x = x-1 pour se ramener à une limite en 0. On obtient alors x(x-1)ln(x), et comme xln(x) tend vers 0, la limite recherchée est égale à 0.
Ces exemples utilisent les propriétés du logarithme pour simplifier les limites. Si vous avez des questions, consultez la FAQ.
Révisions Maths lycée
Analyse Terminale
ECG

Dériver ln(u)
Dans ce cours, nous apprenons à déterminer l'ensemble de définition et à calculer la dérivée d'une fonction contenant des logarithmes. Il est important de toujours faire attention à l'ensemble de définition d'une expression contenant un logarithme, qui est défini uniquement sur Réactoire+.
Nous nous concentrons sur la méthode permettant de déterminer l'ensemble de définition d'une fonction avec un logarithme et de calculer sa dérivée. Parfois, dans un exercice plus long, les élèves oublient de prendre en compte l'ensemble de définition de l'expression à étudier.
Nous examinons tout d'abord la fonction f(x) = ln(8x-4). La fonction ln est définie et dérivable sur R étoile plus. Nous cherchons ensuite les valeurs de x pour lesquelles 8x-4 est supérieur à 0, ce qui correspond à x strictement supérieur à 1,5. Ainsi, l'intervalle de définition et de dérivabilité de f est [1,5, +∞[. En simplifiant, nous obtenons que la dérivée de f est 2/(2x-1).
Nous étudions ensuite la fonction f(x) = ln(x² + x + 1), qui est un polynôme de degré 2. Nous examinons son discriminant, qui est strictement négatif, ce qui signifie que le polynôme est toujours positif. Par conséquent, f(x) = ln(g(x)) est définie et dérivable sur R, et g(x) est toujours strictement positif. La dérivée de f est 2x/(x² + x + 1).
Nous considérons ensuite la fonction f(x) = ln(u(x)/v(x)), où u(x) et v(x) sont des fonctions. Nous devons étudier le signe de cette expression pour déterminer quand elle est strictement positive. En simplifiant l'expression, nous obtenons que f est strictement positive sur l'intervalle ]-∞, -2[ U ]1, +∞[. L'intervalle de définition et de dérivabilité de f est donc l'intervalle ]-∞, -2[ U ]1, +∞[. La dérivée de f est (u'(x)v(x) - u''(x)v(x))/(v(x)²).
Enfin, nous examinons la fonction f(x) = ln(e^x), qui fait intervenir le logarithme et l'exponentielle. Comme d'habitude, nous regardons quand l'expression à l'intérieur du logarithme est strictement positive, ce qui correspond à x strictement supérieur à 0. Ainsi, f est définie et dérivable sur R étoile plus. La dérivée de f est 1.
Il est important de se souvenir de vérifier l'ensemble de définition d'une expression contenant un logarithme.
Révisions Maths lycée
Analyse Terminale
ECG
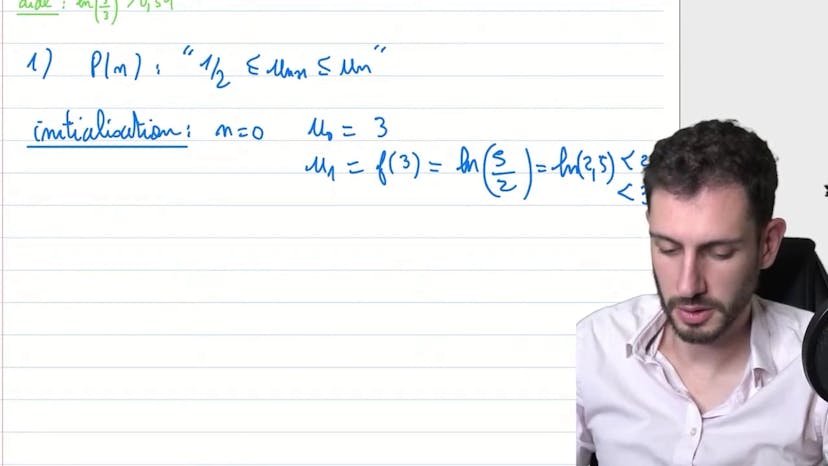
Fonction et suite récurrente associée
Dans cet exercice, nous étudions une fonction définie de manière particulière. Il s'agit d'une fraction rationnelle avec un degré 1 au-dessus de la barre de fraction et un degré 1 en dessous. La fonction est définie sur [0,+∞[.
Nous commençons par déterminer la limite de la fonction lorsque x tend vers +∞. En utilisant une composition de fonctions, nous trouvons que la limite est égale au logarithme de 3.
Ensuite, nous démontrons que la dérivée de la fonction est égale à 3x+3. Nous utilisons la règle de dérivation des fonctions composées pour simplifier le calcul.
Nous concluons que la fonction est strictement croissante et positive, ce qui signifie que f'(x) > 0 pour tout x positif ou nul.
Enfin, nous étudions une suite définie par récurrence en utilisant la fonction f. Nous démontrons par récurrence que la suite est décroissante et minorée par 1/2.
Cet exercice nous permet de prouver des résultats généraux sur l'ensemble de définition de la fonction et d'étudier une suite définie par récurrence.
Révisions Maths lycée
Analyse Terminale
ECG

Un classique de BAC : étude de fonction en 2 temps
Ce cours est une transcription d'une vidéo sur l'étude de fonctions. Il s'agit d'un exercice classique où l'on doit étudier deux fonctions différentes.
Il commence par étudier la fonction G en calculant et en analysant ses limites aux bornes de son ensemble de définition. Il montre que G est définie sur l'ensemble des réels positifs. Il démontre également que la limite de G en 0 est 1 et que la limite de G en plus l'infini est moins l'infini.
Ensuite, il étudie la fonction F en calculant les limites de F aux bornes de son ensemble de définition et en dressant le tableau de variation de F. Il utilise la propriété que log(x)/x^2 tend vers 0 lorsque x tend vers plus l'infini. Il dérive la fonction F et remarque qu'elle est équivalente à la fonction G. Il en déduit le signe de la dérivée de F en fonction de celui de G.
Enfin, il dresse le tableau de variation de F en utilisant les informations sur le signe de G. Il conclut en établissant les limites de F aux bornes de son ensemble de définition.


