Online Primitives & Équations Différentielles course by Top Instructors - Primitives & Équations Différentielles

Introduction ED

L'introduction sur les équations différentielles explique les définitions de base. Une équation différentielle est une équation dans laquelle l'inconnu est une fonction. Les inconnues de l'équation différentielle sont des fonctions, que l'on appelle « petite y », comparativement aux inconnues réelles que l'on appelle « petite x ». Par exemple, pour une fonction donnée « petite f », l'équation « petite y'f» est une primitive permettant de trouver les fonctions qui se dérivent pour former la fonction de base. Les équations différentielles ont des applications fréquentes en physique pour résoudre des problèmes dans lesquels la vitesse de variation d'une grandeur dépend de sa position ou de la valeur de cette grandeur. L'illustration avec un thé qui refroidit est un exemple de la façon dont une équation différentielle peut être utilisée pour décrire ce processus. Les méthodes pour résoudre les équations différentielles comprennent les équations homogènes, les équations linéaires simples et une méthode qui combine les deux. Les solutions peuvent être des fonctions de base, telles que y'ay pour les équations homogènes, y'ay'b pour une linéaire simple, ou la méthode y'ay'ay'y'b'y'y'b'y'b'y'b' pour les deux. Les équations différentielles sont courantes en physique et en mathématiques, et leur résolution est un sujet important pour de nombreuses applications pratiques.

ED : définitions de base

Dans ce cours, on apprend les équations différentielles homogènes, qui sont des équations de la forme y'à y avec un réel non nul. Les solutions de ces équations prennent la forme k fois exponentielle à x, où k peut être n'importe quel réel non nul. Cependant, si on fixe un point de départ y0 à la fonction, il n'y a qu'une seule fonction exponentielle à x qui vérifie f de x0 égal y0.La démonstration pour trouver les solutions exponentielles à x commence en posant une g de x égale exponentielle moins a à x fois f de x. Ensuite, on montre que g est une constante en dérivant et en montrant que g' est égal à 0. Enfin, on dégage la constante c dans f' de x égale c fois exponentielle ax pour trouver la solution complète.Il est à noter que la méthode de la démonstration est utilisée pour mieux comprendre comment les résultats sont obtenus et sa nécessité doit être respectée, même si elle paraît complexe. De plus, cela peut aider les étudiants à résoudre les problèmes.

Solutions Particulières

En bref, les équations différentielles non homogènes ont la forme Y'=Ay+F, où F peut être n'importe quelle fonction. La solution à cela est la somme d'une solution homogène Y'=Ay et d'une solution particulière U, telle que U'=Ay+F. Il existe des cas où U peut être trouvée en s'inspirant de la famille de la fonction F, par exemple, si F est une fonction affine, U sera une fonction affine aussi. Le cas le plus simple à retenir du programme est celui où F est constante, où la solution particulière est U=(-B/A), qui est constante. Ajouter cette solution particulière à la solution homogène donne la solution générale à l'équation. La démonstration de ce cas est que U=C, avec C constant, est posée dans l'équation et résolue pour trouver que la seule valeur possible de C est (-B/A).

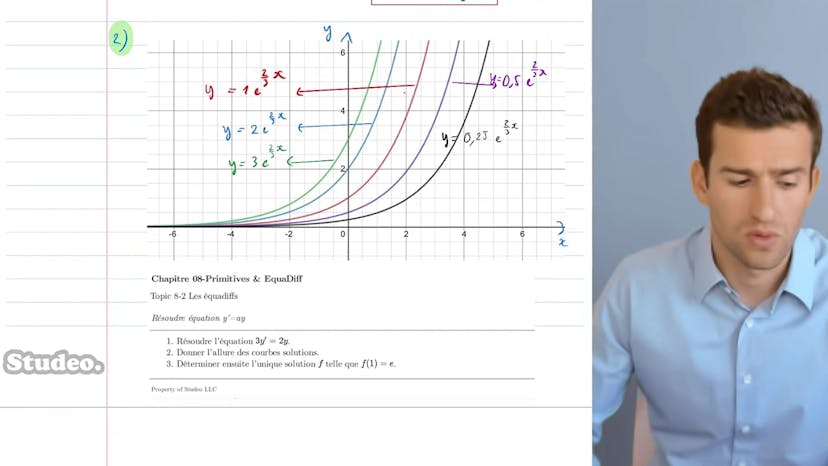
Équation y'=ay

Dans cette méthode, il est expliqué comment résoudre une équation différentielle de premier ordre à coefficient constant. L'équation y' = y est étudiée plus spécifiquement, où dans cet exemple particulier, on a 3y' = 2y. Après avoir divisé par 3, on obtient y' = 2/3 y, ce qui correspond à la forme y' = y avec a = 2/3. On sait que les solutions sont de la forme k * e^(ax), donc dans ce cas k * e^(2/3 x), avec k appartenant à R réel. Ensuite, on nous demande de donner l'allure des courbes solutions en faisant varier la constante k. Des exemples sont donnés avec différentes valeurs de k, où on voit que plus k augmente, plus la courbe se "décolle" et devient une exponentielle avec une constante multiplicative. Toutes ces courbes ont la même allure. Ensuite, on nous demande de trouver la courbe qui vérifie f(1) = e. On sait que lorsque l'on a une condition particulière, il y aura une solution unique qui vérifiera à la fois l'équation différentielle et cette condition. Ici, on veut que f(1) = e, donc on cherche à déterminer la valeur de k. En remplaçant x par 1 dans la fonction f(x), on obtient une équation simple en k, qu'on résout pour trouver k = e^(1/3). Ainsi, la solution de l'équation différentielle avec la condition f(1) = e est f(x) = e^(1/3) * e^(2/3 x). Il s'agit d'une méthode classique pour résoudre une équation différentielle du type y' = y avec une condition initiale. Pour plus de détails, référez-vous à la FAQ en cas de questions.

Équation y'=ay+b

Dans cette vidéo, l'objectif est de présenter la méthode de résolution des équations différentielles d'ordre 1 avec un second membre, en utilisant l'exemple de y' = y + b. La méthode consiste à chercher une solution particulière constante, puis à résoudre l'équation homogène y' = y. Ensuite, il suffit de faire la somme des deux solutions. Pour l'exemple y' = -y + 3, la solution homogène est y = ae^(-x). Ensuite, la solution particulière constante est phi = 3. Ainsi, toutes les solutions sont de la forme y = e^(-x) + 3 (avec une constante multiplicative quelconque). Il est important de noter qu'il y a toujours une constante multiplicative et que pour la déterminer, une condition particulière est nécessaire. Si vous avez des questions, n'hésitez pas à les poser dans la description.

Équation y'=ay+φ

Dans ce cours, nous apprenons à résoudre une équation différentielle de la forme y = y + phi, où phi est une fonction qui n'est pas constante. Pour trouver la solution particulière, nous utilisons la méthode habituelle de trouver une solution particulière et de la sommer à l'équation homogène y = y. Cependant, nous ne cherchons pas une solution particulière sous une forme constante et avons besoin d'un petit indice pour la trouver. On nous demande ensuite de montrer que f est solution de E équivaut à f - p solution de E', où E' est l'équation sans le second ordre et f et p sont des fonctions. Nous isolons ensuite f pour trouver la solution de E. Nous remarquons que nous avons toujours la constante multiplicative inconnue, mais nous avons besoin de conditions particulières dans notre fonction pour la trouver.

Second membre en exponentielle

Les équations différentielles sont essentielles dans les études d'ingénieur. Pour résoudre une équation du premier ordre sans second membre, on divise la solution en deux parties : la solution sans second membre (SSM) et une solution particulière. La SSM est généralement de la forme exponential de x, tandis que la solution particulière dépend de la nature de la fonction Phi(x). On peut trouver la solution particulière en choisissant une fonction de la même forme que Phi(x) et en complexifiant si nécessaire. Si Phi(x) est une somme de termes, on peut séparer la solution en plusieurs parties en utilisant le principe de superposition. En résumé, pour résoudre une équation différentielle, on trouve d'abord la solution SSM puis une solution particulière en fonction de Phi(x) et on combine les deux pour obtenir la solution générale.

Solution particulière : trigonométrie

Dans ce cours, nous étudions une équation différentielle donnée. Il est suggéré de trouver une solution particulière en utilisant la forme donnée dans la question. Cependant, en essayant la forme suggérée, on se rend compte que cela ne fonctionne pas car cela produit un terme sin alors que nous avons besoin d'un terme cos. La meilleure technique est donc de combiner à la fois du cos et du sin, comme suggéré dans la question. En identifiant les termes en cos et en sin, nous obtenons les coefficients correspondants. Ensuite, nous pouvons déduire l'ensemble des solutions en ajoutant le terme correspondant à l'équation sans second membre. La solution générale est donc la somme de la solution particulière et de la solution sans second membre. C'est un principe de base dans les équations différentielles, où la recherche de la solution particulière peut être plus difficile dans les exercices plus avancés.